Ramon.codina (talk | contribs) m (Ramon.codina moved page Villota Codina 2020a to Villota Codina 2020b) |
|||
| (21 intermediate revisions by the same user not shown) | |||
| Line 15: | Line 15: | ||
==Abstract== | ==Abstract== | ||
| − | + | In this article we present the approximation of the coupled model of the equations of motion of a fluid in shallow waters with the convection-diffusion-reaction (CDR) equation of pollutant transport. This approximation is carried out using high order finite elements and using stabilised variational sub-scale methods. We write the coupled system of equations, previously discretised in time and linearised, as a transient vector equation of CDR. The stabilised finite element methods used are the known ASGS and OSS sub-scale methods, the same ones that allow us to use the same interpolation for all unknowns, as well as to deal with dominant convection and reaction flows. We consider the possibility of non-linearity in both the convective and reaction terms. We will not consider the possible development of shocks in the solution. In order to examine the accuracy and robustness of the ASGS and OSS methods, we present four test cases: mesh convergence, transport of a pollutant in a square cavity, transport of a pollutant in the Gulf of Roses and at the river Guadalquivir mouth, and the predator-prey model, which can be written as a transient CDR vector equation with non-linearity in the reaction term. | |
'''Keywords''': Shallow waters, softening and stabilization, transport of pollutants, predator-prey model | '''Keywords''': Shallow waters, softening and stabilization, transport of pollutants, predator-prey model | ||
| − | |||
| − | |||
==1. Introducción== | ==1. Introducción== | ||
| Line 131: | Line 129: | ||
===2.2 Cambio de variables=== | ===2.2 Cambio de variables=== | ||
| − | Realizando un cambio de variables, <math display="inline">\varphi _{a,\alpha }:=h\varphi _{\alpha }</math>, <math display="inline">u_{i}:=hU_{i}</math> y <math display="inline">P:=\frac{1}{2}g\left(h^{2}-H^{2}\right)</math>, con <math display="inline">\partial _{t}P=hg\partial _{t}h,</math> las ecuaciones | + | Realizando un cambio de variables, <math display="inline">\varphi _{a,\alpha }:=h\varphi _{\alpha }</math>, <math display="inline">u_{i}:=hU_{i}</math> y <math display="inline">P:=\frac{1}{2}g\left(h^{2}-H^{2}\right)</math>, con <math display="inline">\partial _{t}P=hg\partial _{t}h,</math> las ecuaciones [[#eq-1|(1)]], [[#eq-2|(2)]] y ([[#eq-3|3]]) se pueden escribir de la siguiente manera: |
<span id="eq-8"></span> | <span id="eq-8"></span> | ||
| Line 449: | Line 447: | ||
donde <math display="inline">u_{h}</math> es la aproximación de la incógnita <math display="inline">u</math> en el espacio de elementos finitos, <math display="inline">C</math> es una constante positiva, <math display="inline">h</math> es el diámetro de la partición de elementos finitos (no confundir con la altura de la lámina de agua) y <math display="inline">d</math> el grado polinómico de la función de forma correspondiente a la interpolación de la aproximación <math display="inline">u_{h}</math>. Consideraremos pruebas de convergencia en malla para <math display="inline">1\leq d\leq{4}</math>. | donde <math display="inline">u_{h}</math> es la aproximación de la incógnita <math display="inline">u</math> en el espacio de elementos finitos, <math display="inline">C</math> es una constante positiva, <math display="inline">h</math> es el diámetro de la partición de elementos finitos (no confundir con la altura de la lámina de agua) y <math display="inline">d</math> el grado polinómico de la función de forma correspondiente a la interpolación de la aproximación <math display="inline">u_{h}</math>. Consideraremos pruebas de convergencia en malla para <math display="inline">1\leq d\leq{4}</math>. | ||
| − | Si graficamos la ecuación ([[#eq-20| | + | Si graficamos la ecuación ([[#eq-20|20]]) (en el caso de la igualdad) en el plano, con <math display="inline">\mathrm{log}\,e</math> en las ordenadas y <math display="inline">\mathrm{log}\,h</math> en las abscisas, tenemos una línea recta, donde <math display="inline">d+1</math> es la pendiente teórica óptima de convergencia. Las pruebas de convergencia en malla consisten entonces en verificar que la pendiente calculada sea precisamente <math display="inline">d+1</math>. Para ello, seleccionamos como solución exacta tanto para las velocidades <math display="inline">U_1</math>, <math display="inline">U_2</math> como para la elevación de la superficie libre del agua <math display="inline">\eta </math> y para la concentración de un contaminante <math display="inline">\varphi </math>, la función polinómica espacio-temporal |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 479: | Line 477: | ||
A continuación detallamos los resultados de los experimentos numéricos de las pruebas de convergencia en malla con solución analítica conocida, tanto para el método ASGS como para el OSS. En cada gráfica se puede apreciar con línea continua la pendiente teórica de convergencia y con línea con apéndices sobre ella la pendiente calculada. Presentamos los resultados para los distintos grados polinómicos de las funciones de forma estudiados, es decir, elementos lineales, cuadráticos, cúbicos y de cuarto orden triangulares <math display="inline">P_{1},\;P_{2},\;P_{3},\;P_{4}</math> y elementos cuadrangulares <math display="inline">Q_{1},\;Q_{2},\;Q_{3},\;Q_{4}</math>, respectivamente. | A continuación detallamos los resultados de los experimentos numéricos de las pruebas de convergencia en malla con solución analítica conocida, tanto para el método ASGS como para el OSS. En cada gráfica se puede apreciar con línea continua la pendiente teórica de convergencia y con línea con apéndices sobre ella la pendiente calculada. Presentamos los resultados para los distintos grados polinómicos de las funciones de forma estudiados, es decir, elementos lineales, cuadráticos, cúbicos y de cuarto orden triangulares <math display="inline">P_{1},\;P_{2},\;P_{3},\;P_{4}</math> y elementos cuadrangulares <math display="inline">Q_{1},\;Q_{2},\;Q_{3},\;Q_{4}</math>, respectivamente. | ||
| − | El dominio computacional es el cuadrado <math display="inline">\left[0,1\right]\times \left[0,1\right]</math> y el intervalo de tiempo es <math display="inline">\left[0,1\right]</math>, con incrementos para cada paso de tiempo <math display="inline">\delta t=0.2</math>. La malla de elementos finitos consiste en triángulos o cuadrados formando una malla regular. Para cada grado polinómico de las funciones de forma <math display="inline">P_{1},\;P_{2},\;P_{3},\;P_{4}</math> o <math display="inline">Q_{1},\;Q_{2},\;Q_{3},\;Q_{4},</math> hemos calculado los errores con norma <math display="inline">L^{2}</math> para ocho mallas de tamaño <math display="inline">h</math>, siendo <math display="inline">\frac{1}{h}=15,\;20,\;25,\;30,\;35,\;40,\;45,\;50,</math> el número de partes en que se ha dividido cada lado del cuadrado. En la | + | El dominio computacional es el cuadrado <math display="inline">\left[0,1\right]\times \left[0,1\right]</math> y el intervalo de tiempo es <math display="inline">\left[0,1\right]</math>, con incrementos para cada paso de tiempo <math display="inline">\delta t=0.2</math>. La malla de elementos finitos consiste en triángulos o cuadrados formando una malla regular. Para cada grado polinómico de las funciones de forma <math display="inline">P_{1},\;P_{2},\;P_{3},\;P_{4}</math> o <math display="inline">Q_{1},\;Q_{2},\;Q_{3},\;Q_{4},</math> hemos calculado los errores con norma <math display="inline">L^{2}</math> para ocho mallas de tamaño <math display="inline">h</math>, siendo <math display="inline">\frac{1}{h}=15,\;20,\;25,\;30,\;35,\;40,\;45,\;50,</math> el número de partes en que se ha dividido cada lado del cuadrado. En la [[#table-1|Tabla 1]] se muestran el número de elementos y el número de nodos para cada refinamiento, tanto para elementos triangulares como para elementos cuadrangulares. Los valores de las constantes algorítmcas <math display="inline">c_{i}</math>, <math display="inline">i=1,2,3,4,</math> se han calibrado a <math display="inline">c_{1}=12,</math> <math display="inline">c_{2}=2,</math> <math display="inline">c_{3}=1,</math> <math display="inline">c_{4}=1</math> y el integrador temporal utilizado es BDF3 (diferencias finitas hacia atrás de cuatro niveles de tiempo y tercer orden en <math display="inline">\delta t</math>). |
<div class="center" style="font-size: 75%;">'''Tabla 1'''. Refinamiento para elementos triangulares y cuadrangulares</div> | <div class="center" style="font-size: 75%;">'''Tabla 1'''. Refinamiento para elementos triangulares y cuadrangulares</div> | ||
| Line 622: | Line 620: | ||
En el encabezado de las gráficas de las pruebas de convergencia en malla de las Figuras [[#img-1|1]] y [[#img-2|2]] se adjuntan dos filas con los valores de las pendientes calculadas; la primera fila corresponde a los valores de las pendientes de las rectas que pasan por los primeros 5 puntos y la segunda fila son las pendientes de las rectas que pasan por los últimos 5 puntos de los 8 puntos del refinamiento de malla evaluados <math display="inline">\left(\frac{1}{h}=15,\;20,\;25,\;30,\;35,\;40,\;45,\;50\right)</math>. De esta manera podemos visualizar numéricamente la tendencia de la convergencia de las pendientes calculadas hacia el valor teórico. Para el cálculo de dichas pendientes se ha utilizado el método de los mínimos cuadrados; la simbología <math display="inline">m(P1),</math> <math display="inline">m(P2),</math> <math display="inline">m(P3),</math> <math display="inline">m(P4),</math> corresponde a las pendientes para elementos triangulares: lineales, cuadráticos, cúbicos y de cuarto orden respectivamente, mientras que para elementos cuadrangulares lineales, cuadráticos, cúbicos y de cuarto orden la simbología es <math display="inline">m(Q1),</math> <math display="inline">m(Q2),</math> <math display="inline">m(Q3),</math> <math display="inline">m(Q4)</math>. Los valores de las pendientes teóricas para las variables de la velocidad y de concentración de un contaminante son <math display="inline">m(P1)=m(Q1)=2</math>, <math display="inline">m(P2)=m(Q2)=3</math>, <math display="inline">m(P3)=m(Q3)=4</math>, <math display="inline">m(P4)=m(Q4)=5</math>, y las pendientes teóricas para la variable <math display="inline">\eta </math>, que es la elevación de la superficie libre del agua, son <math display="inline">m(P1)=m(Q1)=1</math>, <math display="inline">m(P2)=m(Q2)=2</math>, <math display="inline">m(P3)=m(Q3)=3</math>, <math display="inline">m(P4)=m(Q4)=4</math>. | En el encabezado de las gráficas de las pruebas de convergencia en malla de las Figuras [[#img-1|1]] y [[#img-2|2]] se adjuntan dos filas con los valores de las pendientes calculadas; la primera fila corresponde a los valores de las pendientes de las rectas que pasan por los primeros 5 puntos y la segunda fila son las pendientes de las rectas que pasan por los últimos 5 puntos de los 8 puntos del refinamiento de malla evaluados <math display="inline">\left(\frac{1}{h}=15,\;20,\;25,\;30,\;35,\;40,\;45,\;50\right)</math>. De esta manera podemos visualizar numéricamente la tendencia de la convergencia de las pendientes calculadas hacia el valor teórico. Para el cálculo de dichas pendientes se ha utilizado el método de los mínimos cuadrados; la simbología <math display="inline">m(P1),</math> <math display="inline">m(P2),</math> <math display="inline">m(P3),</math> <math display="inline">m(P4),</math> corresponde a las pendientes para elementos triangulares: lineales, cuadráticos, cúbicos y de cuarto orden respectivamente, mientras que para elementos cuadrangulares lineales, cuadráticos, cúbicos y de cuarto orden la simbología es <math display="inline">m(Q1),</math> <math display="inline">m(Q2),</math> <math display="inline">m(Q3),</math> <math display="inline">m(Q4)</math>. Los valores de las pendientes teóricas para las variables de la velocidad y de concentración de un contaminante son <math display="inline">m(P1)=m(Q1)=2</math>, <math display="inline">m(P2)=m(Q2)=3</math>, <math display="inline">m(P3)=m(Q3)=4</math>, <math display="inline">m(P4)=m(Q4)=5</math>, y las pendientes teóricas para la variable <math display="inline">\eta </math>, que es la elevación de la superficie libre del agua, son <math display="inline">m(P1)=m(Q1)=1</math>, <math display="inline">m(P2)=m(Q2)=2</math>, <math display="inline">m(P3)=m(Q3)=3</math>, <math display="inline">m(P4)=m(Q4)=4</math>. | ||
| − | En la | + | En la [[#img-1|Figura 1]], se muestra la convergencia en malla para la primera componente de la velocidad usando elementos triangulares y en la [[#img-2|Figura 2]] la convergencia en malla para la concentración de un contaminante. Las otras variables muestran igualmente convergencia óptima para todos los elementos considerados. Lo mismo sucede con los elementos cuadrangulares. |
<div id='img-1'></div> | <div id='img-1'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: auto;" |
|- | |- | ||
| − | |[[Image:Draft_Codina_913592092-test-ASGS_U1.png|600px|]] | + | |style="padding-top:10px;" | [[Image:Draft_Codina_913592092-test-ASGS_U1.png|600px|]] |
| − | |[[Image:Draft_Codina_913592092-test-OSS_U1.png|600px|Convergencia en malla ASGS-OSS, elementos triangulares, velocidad U₁.]] | + | |style="padding-top:10px;" | [[Image:Draft_Codina_913592092-test-OSS_U1.png|600px|Convergencia en malla ASGS-OSS, elementos triangulares, velocidad U₁.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" | '''Figura 1'''. Convergencia en malla ASGS-OSS, elementos triangulares, velocidad <math>U_1</math> | + | | colspan="2" style="padding-bottom:10px;" | '''Figura 1'''. Convergencia en malla ASGS-OSS, elementos triangulares, velocidad <math>U_1</math> |
|} | |} | ||
<div id='img-2'></div> | <div id='img-2'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: auto;" |
|- | |- | ||
| − | |[[Image:Draft_Codina_913592092-test-ASGS_fi.png|600px|]] | + | |style="padding-top:10px;" | [[Image:Draft_Codina_913592092-test-ASGS_fi.png|600px|]] |
| − | |[[Image:Draft_Codina_913592092-test-OSS_fi.png|600px|Convergencia en malla ASGS-OSS, elementos triangulares, concentración φ.]] | + | |style="padding-top:10px;" | [[Image:Draft_Codina_913592092-test-OSS_fi.png|600px|Convergencia en malla ASGS-OSS, elementos triangulares, concentración φ.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" | '''Figura 2'''. Convergencia en malla ASGS-OSS, elementos triangulares, concentración <math>\varphi </math> | + | | colspan="2" style="padding-bottom:10px;" | '''Figura 2'''. Convergencia en malla ASGS-OSS, elementos triangulares, concentración <math>\varphi </math> |
|} | |} | ||
| Line 646: | Line 644: | ||
Este caso de referencia ha sido ampliamente examinado en la literatura con diferentes métodos, en <span id='citeF-6'></span>[[#cite-6|[6]]] con el método de diferencias finitas, con el método de volúmenes finitos en <span id='citeF-3'></span><span id='citeF-5'></span>[[#cite-3|[3,5]]], con el método SUPG en <span id='citeF-4'></span>[[#cite-4|[4]]]; en todos los casos se ha considerado convección pura, es decir, el coeficiente empírico de dispersión del transporte de un contaminante se ha tomado nulo. En el presente trabajo vamos a reexaminar el caso de referencia con el método variacional ASGS y utilizando funciones de forma cuadráticas, cúbicas y de cuarto orden, en convección dominante, es decir, considerando el coeficiente empírico de dispersión <math display="inline">k_{11}=k_{22}=10^{-3}</math> <math display="inline">\mathrm{m^{2}/s}</math> y <math display="inline">k_{12}=k_{21}=0</math> <math display="inline">\mathrm{m^{2}/s}</math>. | Este caso de referencia ha sido ampliamente examinado en la literatura con diferentes métodos, en <span id='citeF-6'></span>[[#cite-6|[6]]] con el método de diferencias finitas, con el método de volúmenes finitos en <span id='citeF-3'></span><span id='citeF-5'></span>[[#cite-3|[3,5]]], con el método SUPG en <span id='citeF-4'></span>[[#cite-4|[4]]]; en todos los casos se ha considerado convección pura, es decir, el coeficiente empírico de dispersión del transporte de un contaminante se ha tomado nulo. En el presente trabajo vamos a reexaminar el caso de referencia con el método variacional ASGS y utilizando funciones de forma cuadráticas, cúbicas y de cuarto orden, en convección dominante, es decir, considerando el coeficiente empírico de dispersión <math display="inline">k_{11}=k_{22}=10^{-3}</math> <math display="inline">\mathrm{m^{2}/s}</math> y <math display="inline">k_{12}=k_{21}=0</math> <math display="inline">\mathrm{m^{2}/s}</math>. | ||
| − | El dominio computacional es un canal cuadrado de 9 | + | El dominio computacional es un canal cuadrado de 9 km <math display="inline">\times 9</math> km. En cuanto al mallado, con el objeto de comparar los resultados entre elementos lineales y de alto orden, hemos considerado conveniente utilizar refinamientos de malla para elementos <math display="inline">Q_{1},</math> <math display="inline">Q_{2},</math> <math display="inline">Q_{3}</math> y <math display="inline">Q_{4}</math> que den el mismo número de nodos entre si. Tomamos como referencia el refinamiento de malla para <math display="inline">Q_{2}</math>, que consta de <math display="inline">90 \times 90</math> elementos cuadrados uniformes de 9 nodos, es decir, el espaciado en las direcciones <math display="inline">x</math> e <math display="inline">y</math> es <math display="inline">\delta x=\delta y=100</math> <math display="inline">\mathrm{m}</math>, con un total de 8100 elementos y 32761 nodos. De esta manera, la malla de referencia para elementos <math display="inline">Q_{1}</math> consta de 180<math display="inline">\times </math>180 elementos cuadrados uniformes de 4 nodos, es decir <math display="inline">\delta x=\delta y=50</math> <math display="inline">\mathrm{m}</math>, con un total de 32400 elementos y 32761 nodos. La malla de referencia para elementos <math display="inline">Q_{3}</math> consta de <math display="inline">60 \times 60</math> elementos cuadrados uniformes de 16 nodos, es decir <math display="inline">\delta x=\delta y=150</math> <math display="inline">\mathrm{m}</math>, con un total de 3600 elementos y 32761 nodos. Finalmente, la malla de referencia para elementos <math display="inline">Q_{4}</math> consta de 45<math display="inline">\times </math>45 elementos cuadrados uniformes de 25 nodos, es decir <math display="inline">\delta x=\delta y=200</math> <math display="inline">\mathrm{m}</math>, con un total de 2025 elementos y 32761 nodos. |
El tamaño del paso de tiempo es uniforme, con <math display="inline">\delta t=20</math> <math display="inline">\mathrm{s}</math>, y el integrador temporal es BDF3 en todos los casos. | El tamaño del paso de tiempo es uniforme, con <math display="inline">\delta t=20</math> <math display="inline">\mathrm{s}</math>, y el integrador temporal es BDF3 en todos los casos. | ||
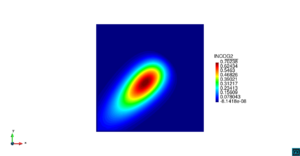
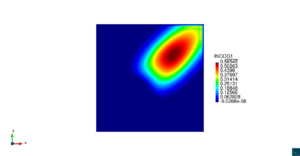
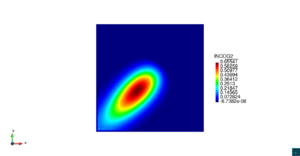
| Line 665: | Line 663: | ||
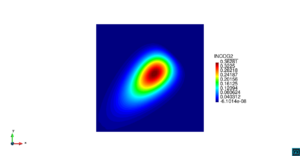
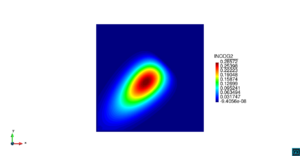
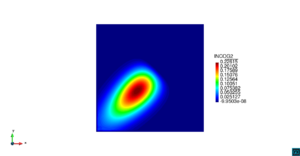
Dada la baja difusión del problema, la solución exacta es aquella concentración de contaminante que se mueve diagonalmente a través del dominio con velocidad constante, preservándose su forma durante todo el tiempo. La Figura [[#img-3|3]] ilustra los resultados usando el elemento <math display="inline">Q_{2}</math> comparados con la solución teórica en diferentes tiempos, observándose en todos los casos resultados completamente satisfactorios comparados con la solución exacta. | Dada la baja difusión del problema, la solución exacta es aquella concentración de contaminante que se mueve diagonalmente a través del dominio con velocidad constante, preservándose su forma durante todo el tiempo. La Figura [[#img-3|3]] ilustra los resultados usando el elemento <math display="inline">Q_{2}</math> comparados con la solución teórica en diferentes tiempos, observándose en todos los casos resultados completamente satisfactorios comparados con la solución exacta. | ||
| − | En la | + | En la [[#table-2|Tabla 2]], presentamos los valores máximos y mínimos de concentración de contaminante para las funciones de forma <math display="inline">Q_{1}</math>, <math display="inline">Q_{2}</math>, <math display="inline">Q_{3}</math> y <math display="inline">Q_{4}</math>, en donde observamos que a partir de <math display="inline">Q_{2}</math> el error de aproximación al valor exacto máximo es del orden de las centésimas, por lo cual en la [[#img-3|Figura 3]] hemos usado los resultados del elemento <math display="inline">Q_{2}</math>. |
<div id='img-3'></div> | <div id='img-3'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" |
|- | |- | ||
| − | |[[Image:Draft_Codina_913592092-test-1600_3D.png|600px|]] | + | |style="padding:10px;" | [[Image:Draft_Codina_913592092-test-1600_3D.png|600px|]] |
| − | |[[Image:Draft_Codina_913592092-test-1600_corte_x.png|480px|]] | + | |style="padding:10px;" | [[Image:Draft_Codina_913592092-test-1600_corte_x.png|480px|]] |
|- | |- | ||
|[[Image:Draft_Codina_913592092-test-4800_3D.png|600px|]] | |[[Image:Draft_Codina_913592092-test-4800_3D.png|600px|]] | ||
|[[Image:Draft_Codina_913592092-test-4800_corte_x.png|480px|]] | |[[Image:Draft_Codina_913592092-test-4800_corte_x.png|480px|]] | ||
|- | |- | ||
| − | |[[Image:Draft_Codina_913592092-test-9600_3D.png|600px|]] | + | |style="padding:10px;" | [[Image:Draft_Codina_913592092-test-9600_3D.png|600px|]] |
| − | |[[Image:Draft_Codina_913592092-test-9600_corte_x.png|480px|Contornos 3D (izquierda) y distribución del contaminante (derecha) a lo largo de la diagonal de la cavidad cuadrada, con elementos Q₂.]] | + | |style="padding:10px;" | [[Image:Draft_Codina_913592092-test-9600_corte_x.png|480px|Contornos 3D (izquierda) y distribución del contaminante (derecha) a lo largo de la diagonal de la cavidad cuadrada, con elementos Q₂.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" | '''Figura 3'''. Contornos 3D (izquierda) y distribución del contaminante (derecha) a lo largo de la diagonal de la cavidad cuadrada, con elementos <math>Q_2</math> | + | | colspan="2" style="padding:10px;" | '''Figura 3'''. Contornos 3D (izquierda) y distribución del contaminante (derecha) a lo largo de la diagonal de la cavidad cuadrada, con elementos <math>Q_2</math> |
|} | |} | ||
| − | + | <div class="center" style="font-size: 75%;">'''Tabla 2'''. Valores máximos y mínimos de concentración de contaminante en la cavidad cuadrada para <math>t=9600</math> s</div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | <div id='tab-1'></div> | ||
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! !! Solución exacta !! <math>Q_{1}</math> !! <math>Q_{2}</math> !! <math>Q_{3}</math> !! <math>Q_{4}</math> | ||
| + | |- style="text-align:center" | ||
| + | | style="text-align:left;" | Número de elementos | ||
| + | | - | ||
| + | | 32400 | ||
| + | | 8100 | ||
| + | | 3600 | ||
| + | | 2025 | ||
| + | |- style="text-align:center" | ||
| + | | style="text-align:left;" |Número de nodos | ||
| + | | - | ||
| + | | 32761 | ||
| + | | 32761 | ||
| + | | 32761 | ||
| + | | 32761 | ||
| + | |- style="text-align:center" | ||
| + | | style="text-align:left;" |Máximo valor de <math display="inline">\varphi </math> | ||
| + | | 10 | ||
| + | | 9.312 | ||
| + | | 9.976 | ||
| + | | 10.03 | ||
| + | | 10.04 | ||
| + | |- style="text-align:center" | ||
| + | | style="text-align:left;" | Mínimo valor de <math display="inline">\varphi </math> | ||
| + | | 0 | ||
| + | | <math>-0.01032</math> | ||
| + | | <math>-3.702\times{10}^{-10}</math> | ||
| + | | <math>-2.986\times{10}^{-5}</math> | ||
| + | | <math>-3.533\times{10}^{-6}</math> | ||
|} | |} | ||
| Line 728: | Line 722: | ||
Consideramos una concentración constante de un solo contaminante <math display="inline">\varphi=1</math> en el flujo de entrada y coeficientes de difusión constantes <math display="inline">k_{11}=k_{22}=10^{-3}</math> <math display="inline">\mathrm{m^{2}/s}</math> y <math display="inline">k_{12}=k_{21}=0</math> <math display="inline">\mathrm{m^{2}/s}</math>. La suposición de que los coeficientes de difusión son constantes es debido a que los efectos de turbulencia no han sido considerados en el modelo. También asumimos que la concentración del contaminante se anula en las fronteras sólidas, por lo que prescribimos a cero dicha concentración tanto en el perfil de las costas como en las riveras del río, en los dos problemas tratados. En el resto de los contornos consideramos la concentración de contaminante libre, con concentración inicial igual a cero. En ambos ejemplos numéricos hemos considerado batimetría constante con una profundidad de <math display="inline">H=20.0</math> m (no hemos considerado pues la disminución de la profundidad hasta <math display="inline">H=0</math>), la aceleración de la gravedad <math display="inline">g=10</math> m/s<math display="inline">^{2}</math> y la viscosidad cinemática <math display="inline">\nu _{H}=10^{-6}</math> m<math display="inline">^{2}</math>/s. El parámetro de Coriolis <math display="inline">\hat{f}</math>, las tensiones de superficie libre debidas al viento <math display="inline">\tau _{3i}^{s}</math>, las variaciones de presión atmosférica <math display="inline">p_{a}</math> y el coeficiente de fricción en el fondo <math display="inline">\mbox{Ch}</math> no han sido tomados en cuenta en ninguno de los dos ejemplos. | Consideramos una concentración constante de un solo contaminante <math display="inline">\varphi=1</math> en el flujo de entrada y coeficientes de difusión constantes <math display="inline">k_{11}=k_{22}=10^{-3}</math> <math display="inline">\mathrm{m^{2}/s}</math> y <math display="inline">k_{12}=k_{21}=0</math> <math display="inline">\mathrm{m^{2}/s}</math>. La suposición de que los coeficientes de difusión son constantes es debido a que los efectos de turbulencia no han sido considerados en el modelo. También asumimos que la concentración del contaminante se anula en las fronteras sólidas, por lo que prescribimos a cero dicha concentración tanto en el perfil de las costas como en las riveras del río, en los dos problemas tratados. En el resto de los contornos consideramos la concentración de contaminante libre, con concentración inicial igual a cero. En ambos ejemplos numéricos hemos considerado batimetría constante con una profundidad de <math display="inline">H=20.0</math> m (no hemos considerado pues la disminución de la profundidad hasta <math display="inline">H=0</math>), la aceleración de la gravedad <math display="inline">g=10</math> m/s<math display="inline">^{2}</math> y la viscosidad cinemática <math display="inline">\nu _{H}=10^{-6}</math> m<math display="inline">^{2}</math>/s. El parámetro de Coriolis <math display="inline">\hat{f}</math>, las tensiones de superficie libre debidas al viento <math display="inline">\tau _{3i}^{s}</math>, las variaciones de presión atmosférica <math display="inline">p_{a}</math> y el coeficiente de fricción en el fondo <math display="inline">\mbox{Ch}</math> no han sido tomados en cuenta en ninguno de los dos ejemplos. | ||
| + | |||
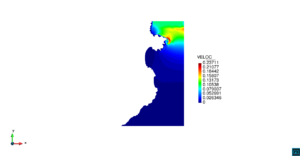
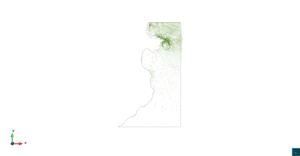
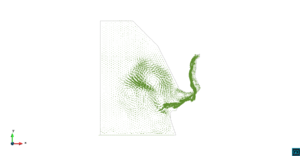
| + | El primer ejemplo es la simulación del transporte de un contaminante de concentración constante <math display="inline">\varphi=1</math>, debido a una corriente marina que viene desde el norte en el golfo de Roses sobre la costa catalana, al sur del Cabo de Creus. La geometría del problema y los resultados numéricos se muestran en las Figuras [[#img-4|4]], [[#img-5|5]] y [[#img-6|6]]. El dominio de simulación tiene dimensiones de aproximadamente 80 <math display="inline">\times </math> 40 km<math display="inline">^{2}</math>. La malla de elementos finitos consiste en 6062 elementos triangulares lineales con 3217 nodos. | ||
| + | |||
| + | Una corriente marina de 0.1 m/s que llega desde el norte ha sido prescrita en el borde superior del dominio. Esto corresponde a una velocidad como flujo de entrada en la parte superior del dominio. En la costa la velocidad se prescribe a cero, mientras que en los contornos inferior y derecho del dominio se deja libre, donde la sobreelevación del agua se prescribe a cero. | ||
<div id='img-4'></div> | <div id='img-4'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" |
|- | |- | ||
| − | |[[Image:Draft_Codina_913592092-test-malla.png|600px|Golfo de Roses. Geometría y malla de elementos finitos.]] | + | |style="padding:5px;" | [[Image:Draft_Codina_913592092-test-malla.png|600px|Golfo de Roses. Geometría y malla de elementos finitos.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | ''' | + | | colspan="1" style="padding:10px;-bottom" | '''Figura 4'''. Golfo de Roses. Geometría y malla de elementos finitos |
|} | |} | ||
| − | |||
| − | |||
| − | |||
<div id='img-5'></div> | <div id='img-5'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" |
|- | |- | ||
| | | | ||
{| style="text-align: center; margin: 1em auto;min-width:50%;width:100%;" | {| style="text-align: center; margin: 1em auto;min-width:50%;width:100%;" | ||
|- | |- | ||
| − | | <math>t</math>=50000 s | + | | <math>t</math>=50000 s |
| − | | [[Image:Draft_Codina_913592092-test-velocidad_50000.png|300px|Creus/velocidad_50000]] | + | | style="padding:5px;" | [[Image:Draft_Codina_913592092-test-velocidad_50000.png|300px|Creus/velocidad_50000]] |
| − | | [[Image:Draft_Codina_913592092-test-elevacion_50000.png|300px|Creus/elevacion_50000]] | + | | style="padding:5px;" | [[Image:Draft_Codina_913592092-test-elevacion_50000.png|300px|Creus/elevacion_50000]] |
|- | |- | ||
| <math>t</math>=100000 s | | <math>t</math>=100000 s | ||
| Line 756: | Line 751: | ||
|- | |- | ||
| <math>t</math>=150000 s | | <math>t</math>=150000 s | ||
| − | | [[Image:Draft_Codina_913592092-test-velocidad_50000.png|300px|Creus/velocidad_50000]] | + | | style="padding:5px;" | [[Image:Draft_Codina_913592092-test-velocidad_50000.png|300px|Creus/velocidad_50000]] |
| − | | [[Image:Draft_Codina_913592092-test-elevacion_150000.png|300px|Creus/elevacion_150000]] | + | | style="padding:5px;" | [[Image:Draft_Codina_913592092-test-elevacion_150000.png|300px|Creus/elevacion_150000]] |
|- | |- | ||
| <math>t</math>=200000 s | | <math>t</math>=200000 s | ||
| Line 764: | Line 759: | ||
|- | |- | ||
| | | | ||
| − | | (a) | + | | style="font-size:75%;" | (a) |
| − | | (b) | + | | style="font-size:75%;" |(b) |
| − | + | ||
|} | |} | ||
| − | |||
|- | |- | ||
| − | |||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
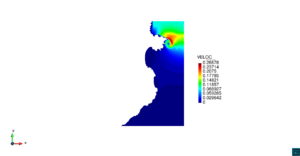
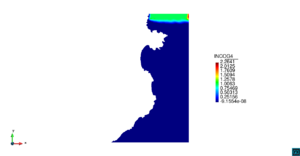
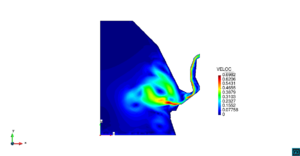
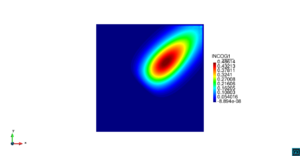
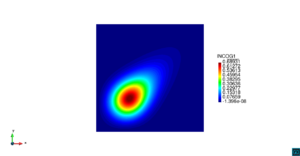
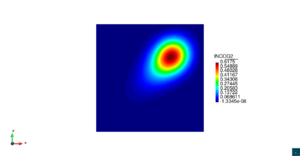
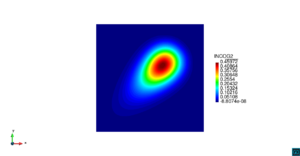
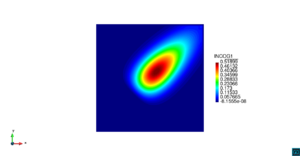
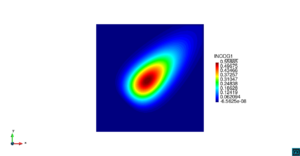
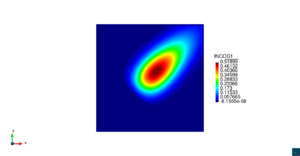
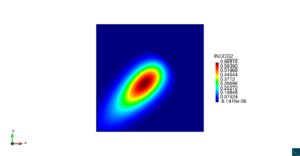
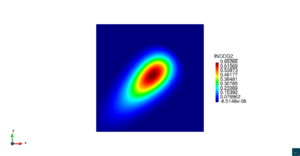
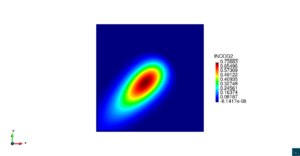
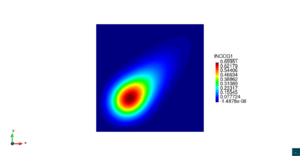
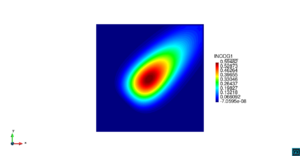
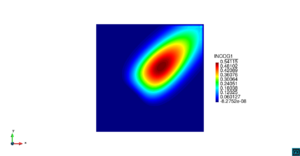
| − | | colspan=" | + | | colspan="3" style="padding:10px;" | '''Figura 5'''. Flujo alrededor del golfo de Roses. (a) Velocidad (máx: 0.29 m/s). (b) Elevación (INCOG3), superficie libre del agua (máx: 2.52 mm, mín: -4.05 mm) |
|} | |} | ||
| + | |||
<div id='img-6'></div> | <div id='img-6'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" |
|- | |- | ||
| | | | ||
{| style="text-align: center; margin: 1em auto;min-width:50%;width:100%;" | {| style="text-align: center; margin: 1em auto;min-width:50%;width:100%;" | ||
|- | |- | ||
| − | | <math>t</math>=50000 s | + | | style="padding-left:5px;" |<math>t</math>=50000 s |
| − | | [[Image:Draft_Codina_913592092-test-vector_velocidad_50000.png|300px|Creus/vector_velocidad_50000]] | + | | [[Image:Draft_Codina_913592092-test-vector_velocidad_50000.png|300px|Creus/vector_velocidad_50000]] |
| − | | [[Image:Draft_Codina_913592092-test-contaminanate_50000.png|300px|Creus/contaminanate_50000]] | + | | [[Image:Draft_Codina_913592092-test-contaminanate_50000.png|300px|Creus/contaminanate_50000]] |
|- | |- | ||
| − | | <math>t</math>=100000 s | + | | style="padding-left:5px;" |<math>t</math>=100000 s |
| [[Image:Draft_Codina_913592092-test-vector_velocidad_100000.png|300px|Creus/vector_velocidad_100000]] | | [[Image:Draft_Codina_913592092-test-vector_velocidad_100000.png|300px|Creus/vector_velocidad_100000]] | ||
| [[Image:Draft_Codina_913592092-test-contaminanate_100000.png|300px|Creus/contaminanate_100000]] | | [[Image:Draft_Codina_913592092-test-contaminanate_100000.png|300px|Creus/contaminanate_100000]] | ||
|- | |- | ||
| − | | <math>t</math>=150000 s | + | | style="padding-left:5px;" |<math>t</math>=150000 s |
| − | | [[Image:Draft_Codina_913592092-test-vector_velocidad_150000.png|300px|Creus/vector_velocidad_150000]] | + | | |[[Image:Draft_Codina_913592092-test-vector_velocidad_150000.png|300px|Creus/vector_velocidad_150000]] |
| − | | [[Image:Draft_Codina_913592092-test-contaminanate_150000.png|300px|Creus/contaminanate_150000]] | + | | [[Image:Draft_Codina_913592092-test-contaminanate_150000.png|300px|Creus/contaminanate_150000]] |
|- | |- | ||
| <math>t</math>=200000 s | | <math>t</math>=200000 s | ||
| Line 798: | Line 791: | ||
|- | |- | ||
| | | | ||
| − | | (a) | + | | style="font-size:75%;" |(a) |
| − | | (b) | + | | style="font-size:75%;" |(b) |
| − | + | ||
|} | |} | ||
| − | |||
|- | |- | ||
| − | |||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
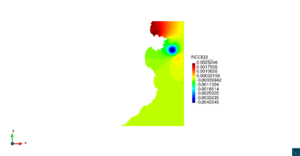
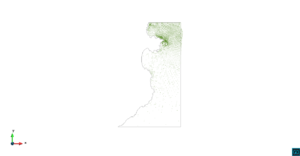
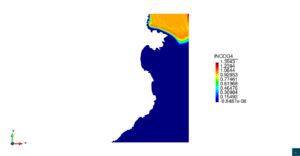
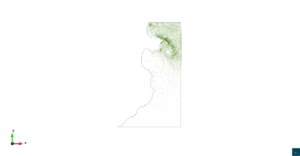
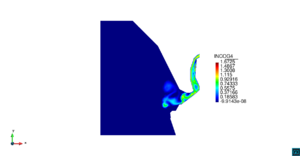
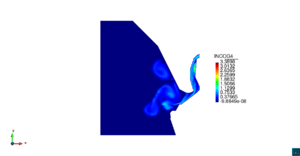
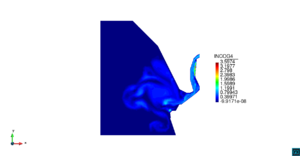
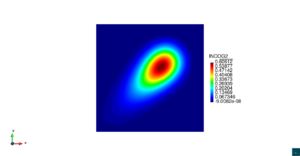
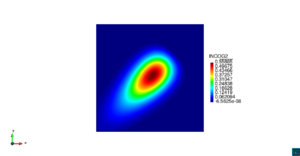
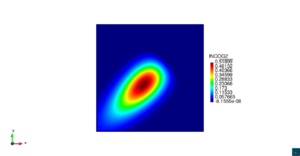
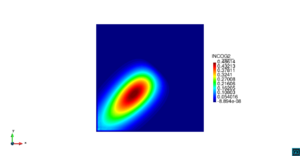
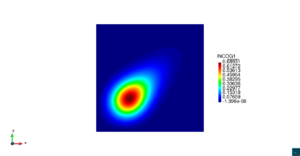
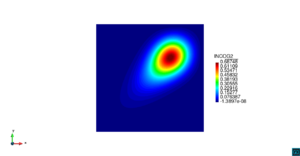
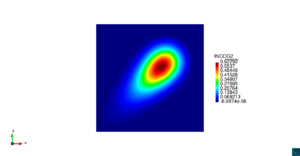
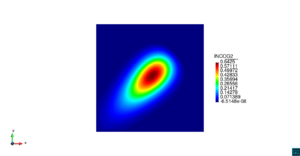
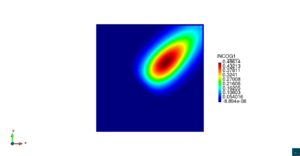
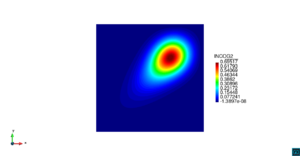
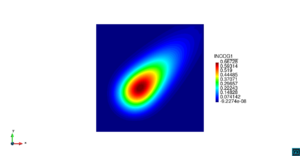
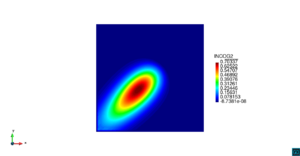
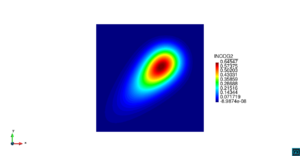
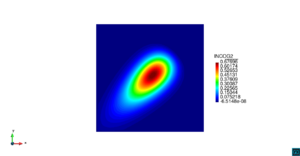
| − | | colspan=" | + | | colspan="3" style="padding-bottom:10px;" | '''Figura 6'''. Flujo alrededor del golfo de Roses. (a) Vectores de velocidad. (b) Concentración del transporte de un contaminante (INGOG 4) |
|} | |} | ||
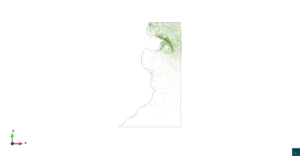
En la segunda simulación numérica consideramos el transporte de un contaminante de concentración constante <math display="inline">\varphi=1</math> en la desembocadura del río Guadalquivir, en la costa del sur de España. La geometría del problema y los resultados numéricos se muestran en las Figuras [[#img-7|7]], [[#img-8|8]] y [[#img-9|9]]. | En la segunda simulación numérica consideramos el transporte de un contaminante de concentración constante <math display="inline">\varphi=1</math> en la desembocadura del río Guadalquivir, en la costa del sur de España. La geometría del problema y los resultados numéricos se muestran en las Figuras [[#img-7|7]], [[#img-8|8]] y [[#img-9|9]]. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<div id='img-7'></div> | <div id='img-7'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" |
|- | |- | ||
| − | |[[Image:Draft_Codina_913592092-test-malla-dup1.png|600px|Desembocadura del río Guadalquivir. Geometría y malla de elementos finitos]] | + | |style="padding:5px;" |[[Image:Draft_Codina_913592092-test-malla-dup1.png|600px|Desembocadura del río Guadalquivir. Geometría y malla de elementos finitos]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | ''' | + | | colspan="1" style="padding-bottom:10px;" | '''Figura 7'''. Desembocadura del río Guadalquivir. Geometría y malla de elementos finitos |
|} | |} | ||
<div id='img-8'></div> | <div id='img-8'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" |
|- | |- | ||
| | | | ||
| Line 847: | Line 816: | ||
|- | |- | ||
| <math>t</math>=50000 s | | <math>t</math>=50000 s | ||
| − | | [[Image:Draft_Codina_913592092-dup1.png|300px|Guadalquivir/velocidad_50000]] | + | | style="padding:5px;" |[[Image:Draft_Codina_913592092-dup1.png|300px|Guadalquivir/velocidad_50000]] |
| − | | [[Image:Draft_Codina_913592092-dup1.png|300px|Guadalquivir/elevacion_50000]] | + | | style="padding:5px;" |[[Image:Draft_Codina_913592092-dup1.png|300px|Guadalquivir/elevacion_50000]] |
|- | |- | ||
| <math>t</math>=100000 s | | <math>t</math>=100000 s | ||
| Line 855: | Line 824: | ||
|- | |- | ||
| <math>t</math>=150000 s | | <math>t</math>=150000 s | ||
| − | | [[Image:Draft_Codina_913592092-test-velocidad_150000.png|300px|Guadalquivir/velocidad_150000]] | + | | style="padding:5px;" |[[Image:Draft_Codina_913592092-test-velocidad_150000.png|300px|Guadalquivir/velocidad_150000]] |
| − | | [[Image:Draft_Codina_913592092-dup1.png|300px|Guadalquivir/elevacion_150000]] | + | | style="padding:5px;" |[[Image:Draft_Codina_913592092-dup1.png|300px|Guadalquivir/elevacion_150000]] |
|- | |- | ||
| <math>t</math>=200000 s | | <math>t</math>=200000 s | ||
| Line 863: | Line 832: | ||
|- | |- | ||
| | | | ||
| − | | (a) | + | | style="font-size:75%;" |(a) |
| − | | (b) | + | | style="font-size:75%;" |(b) |
| − | + | ||
|} | |} | ||
| − | |||
|- | |- | ||
| − | |||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
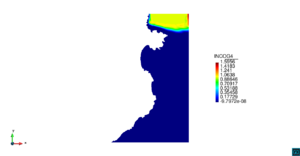
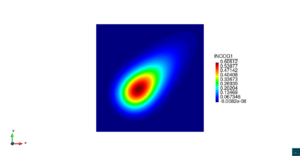
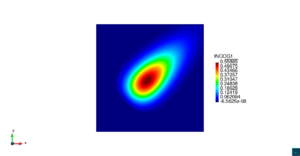
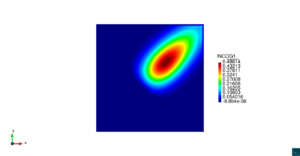
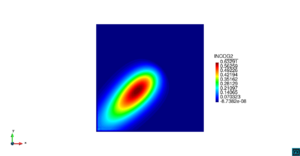
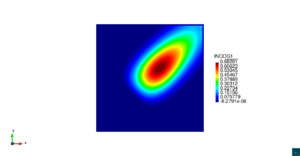
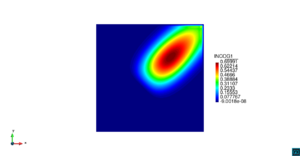
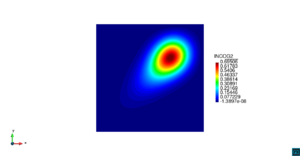
| − | | colspan=" | + | | colspan="3" style="padding:10px;" | '''Figura 8'''. Flujo en la desembocadura del Guadalquivir. (a) Velocidad (máx: 0.83 m/s). (b) Elevación (INCOG3), superficie libre del agua (máx: 1.97 cm, mín: -1.42 cm) |
|} | |} | ||
<div id='img-9'></div> | <div id='img-9'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" |
|- | |- | ||
| | | | ||
{| style="text-align: center; margin: 1em auto;min-width:50%;width:100%;" | {| style="text-align: center; margin: 1em auto;min-width:50%;width:100%;" | ||
|- | |- | ||
| − | | <math>t</math>=50000 s | + | | style="padding-left:5px;" |<math>t</math>=50000 s |
| − | | [[Image:Draft_Codina_913592092-test-vector_velocidad_50002.png|300px|Guadalquivir/vector_velocidad_50002]] | + | | style="padding:5px;" |[[Image:Draft_Codina_913592092-test-vector_velocidad_50002.png|300px|Guadalquivir/vector_velocidad_50002]] |
| − | | [[Image:Draft_Codina_913592092-test-contaminante_50000.png|300px|Guadalquivir/contaminante_50000]] | + | | style="padding:5px;" |[[Image:Draft_Codina_913592092-test-contaminante_50000.png|300px|Guadalquivir/contaminante_50000]] |
|- | |- | ||
| − | | <math>t</math>=100000 s | + | | style="padding-left:5px;" |<math>t</math>=100000 s |
| [[Image:Draft_Codina_913592092-test-vector_velocidad_100002.png|300px|Guadalquivir/vector_velocidad_100002]] | | [[Image:Draft_Codina_913592092-test-vector_velocidad_100002.png|300px|Guadalquivir/vector_velocidad_100002]] | ||
| [[Image:Draft_Codina_913592092-test-contaminante_100000.png|300px|Guadalquivir/contaminante_100000]] | | [[Image:Draft_Codina_913592092-test-contaminante_100000.png|300px|Guadalquivir/contaminante_100000]] | ||
|- | |- | ||
| − | | <math>t</math>=150000 s | + | | style="padding-left:5px;" |<math>t</math>=150000 s |
| [[Image:Draft_Codina_913592092-test-vector_velocidad_150002.png|300px|Guadalquivir/vector_velocidad_150002]] | | [[Image:Draft_Codina_913592092-test-vector_velocidad_150002.png|300px|Guadalquivir/vector_velocidad_150002]] | ||
| [[Image:Draft_Codina_913592092-test-contaminante_150000.png|300px|Guadalquivir/contaminante_150000]] | | [[Image:Draft_Codina_913592092-test-contaminante_150000.png|300px|Guadalquivir/contaminante_150000]] | ||
|- | |- | ||
| − | | <math>t</math>=200000 s | + | | style="padding-left:5px;" |<math>t</math>=200000 s |
| [[Image:Draft_Codina_913592092-test-vector_velocidad_200002.png|300px|Guadalquivir/vector_velocidad_200002]] | | [[Image:Draft_Codina_913592092-test-vector_velocidad_200002.png|300px|Guadalquivir/vector_velocidad_200002]] | ||
| [[Image:Draft_Codina_913592092-test-contaminante_200000.png|300px|Guadalquivir/contaminante_200000]] | | [[Image:Draft_Codina_913592092-test-contaminante_200000.png|300px|Guadalquivir/contaminante_200000]] | ||
|- | |- | ||
| | | | ||
| − | | (a) | + | | style="font-size:75%;" |(a) |
| − | | (b) | + | | style="font-size:75%;" |(b) |
| − | + | ||
|} | |} | ||
| − | |||
|- | |- | ||
| − | |||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
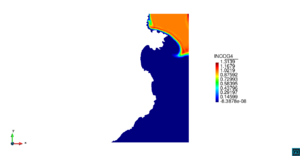
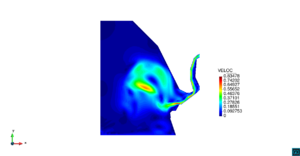
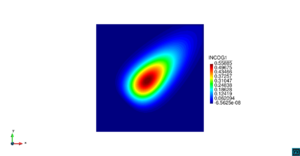
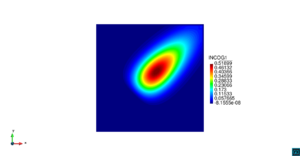
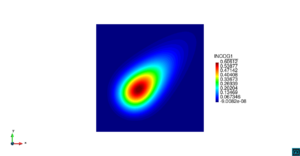
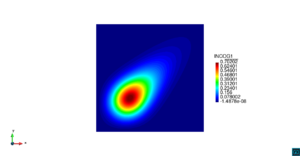
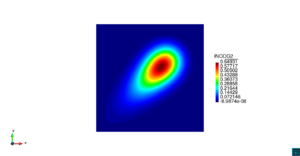
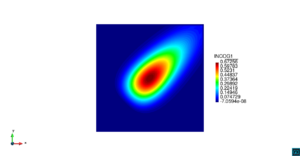
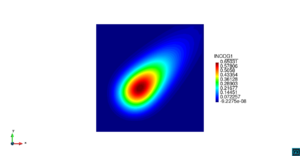
| − | | colspan="1" | ''' | + | | colspan="1" style="padding:10px;" | '''Figura 9'''. Flujo en la desembocadura del Guadalquivir. (a) Vector de velocidad. (b) Concentración del transporte de un contaminante (INGOG 4) |
|} | |} | ||
| + | |||
| + | |||
| + | La malla de elementos finitos consiste en 4955 elementos triangulares lineales con 2645 nodos. | ||
| + | |||
| + | Un flujo de corriente marina de <math display="inline">0.1</math> m/s está prescrito en el contorno inferior en dirección este-oeste y en la desembocadura del río se prescribe una corriente del río de 0.3 m/s, igualmente en dirección este-oeste. En el resto de la costa y en las riveras del río la velocidad se prescribe a cero, y se deja libre en los contornos izquierdo y superior, donde la sobreelevación del agua está prescrita a cero. | ||
| + | |||
| + | Los dos ejemplos numéricos considerados presentan flujos complejos, con importantes variaciones temporales y espaciales. Esto hace que los parámetros de estabilización sean muy variables elemento a elemento. Este hecho dificulta la convergencia de los esquemas iterativos. Puesto que <math display="inline">\tau _1</math> y <math display="inline">\tau _{3}</math> (en el caso de <math display="inline">N=1</math> contaminantes) son escalas de tiempo, a menudo se toman proporcionales a <math display="inline">\delta t</math>, y esto se puede justificar con argumentos diversos <span id='citeF-24'></span>[[#cite-24|[24]]]. En los problemas en los que la convergencia del esquema iterativo es costosa, hemos tomado una cota máxima para <math display="inline">\tau _1</math> y <math display="inline">\tau _3</math> proporcional a <math display="inline">\delta t</math>, de manera que los hemos redefinido en cada elemento <math display="inline">e</math> como | ||
| + | |||
| + | <span id="eq-21"></span> | ||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\tau _{1}^{e}\leftarrow \min (\tau _{1}^{e},\alpha \delta t),\quad \tau _{3}^{e}\leftarrow \min (\tau _{3}^{e},\beta \delta t), </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (21) | ||
| + | |} | ||
| + | |||
| + | donde <math display="inline">\alpha </math> y <math display="inline">\beta </math> son parámetros que hay que ajustar dependiendo del tamaño de la malla y del grado del polinomio de las funciones de forma. El valor de <math display="inline">\tau _{2}^{e}</math> se sigue calculando mediante la expresión dada en ([[#eq-18|18]]). | ||
| + | |||
| + | Mediante experimentación numérica hemos calibrado los parámetros <math display="inline">\alpha </math> y <math display="inline">\beta </math>. Para el primer ejemplo hemos considerado <math display="inline">\alpha=15</math> y <math display="inline">\beta=6</math> con un paso de tiempo uniforme <math display="inline">\delta t=</math>100 s y para el segundo ejemplo <math display="inline">\alpha=3</math> y <math display="inline">\beta=5</math> con <math display="inline">\delta t=</math>2500 s. En ambos casos hemos usado el integrador temporal BDF2 y presentamos resultados numéricos en diferentes instantes de tiempos de simulación, <math display="inline">t=50000,\;100000,\;150000</math> y <math display="inline">200000</math> s. | ||
===4.4 Modelo depredador-presa=== | ===4.4 Modelo depredador-presa=== | ||
| Line 989: | Line 974: | ||
====4.4.2 Pruebas numéricas y resultados==== | ====4.4.2 Pruebas numéricas y resultados==== | ||
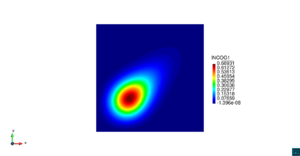
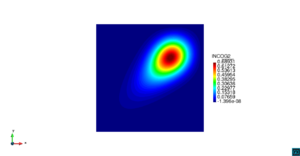
| − | Consideremos la ecuación ([[#eq-22|22]]) del modelo depredador-presa dentro de un cuadrado unitario <math display="inline">\Omega =\left[0,1\right]\times \left[0,1\right]</math>, con condiciones de contorno de Dirichlet homogéneas y condiciones iniciales de las densidades de población de la presa y del depredador dadas por las distribuciones normales ([[#eq-23|23]]) y ([[#eq-24|24]]), respectivamente, escritas a continuación y mostradas en la | + | Consideremos la ecuación ([[#eq-22|22]]) del modelo depredador-presa dentro de un cuadrado unitario <math display="inline">\Omega =\left[0,1\right]\times \left[0,1\right]</math>, con condiciones de contorno de Dirichlet homogéneas y condiciones iniciales de las densidades de población de la presa y del depredador dadas por las distribuciones normales ([[#eq-23|23]]) y ([[#eq-24|24]]), respectivamente, escritas a continuación y mostradas en la [[#img-10|Figura 10]]: |
<span id="eq-23"></span> | <span id="eq-23"></span> | ||
| Line 1,007: | Line 992: | ||
<div id='img-10'></div> | <div id='img-10'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" |
|- | |- | ||
|[[Image:Draft_Codina_913592092-test-Presa_inicial.png|424px|]] | |[[Image:Draft_Codina_913592092-test-Presa_inicial.png|424px|]] | ||
|[[Image:Draft_Codina_913592092-test-Depredador_inicial.png|424px|Condición inicial de la densidad de población de la presa (izquierda) y del depredador (derecha).]] | |[[Image:Draft_Codina_913592092-test-Depredador_inicial.png|424px|Condición inicial de la densidad de población de la presa (izquierda) y del depredador (derecha).]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" | ''' | + | | colspan="2" style="padding-bottom:10px;"| '''Figura 10'''. Condición inicial de la densidad de población de la presa (izquierda) y del depredador (derecha) |
|} | |} | ||
| − | En la | + | En la [[#table-3|Tabla 3]] se encuentran los valores de los coeficientes de reacción <math display="inline">s_{11},</math> <math display="inline">s_{12},</math> <math display="inline">s_{21}</math> y <math display="inline">s_{22}</math> para varios casos de prueba que hemos considerado. Para todos estos casos de prueba los coeficientes de difusión se tomaron como <math display="inline">k_{11}=k_{22}=10^{-4}</math> m<math display="inline">^2</math>/s. El campo de velocidades se mantiene constante tanto para el depredador como para la presa. Las componentes de velocidad de la presa son <math display="inline">a_{11}=0.5</math> m/s, <math display="inline">a_{12}=0.5</math> m/s y para el depredador son <math display="inline">a_{21}=-0.5</math> m/s, <math display="inline">a_{22}=-0.5</math> m/s, con lo cual las poblaciones del depredador y de la presa son conducidas en direcciones opuestas para encontrarse frente a frente una con la otra. No consideramos ningún término fuente y las constantes <math display="inline">\alpha _{1}</math> y <math display="inline">\alpha _{2}</math> se tomaron a la unidad. Con esto el sistema de ecuaciones del modelo depredador-presa se escribe: |
<span id="eq-25"></span> | <span id="eq-25"></span> | ||
| Line 1,028: | Line 1,013: | ||
|} | |} | ||
| + | <div class="center" style="font-size: 75%;">'''Tabla 3'''. Casos de prueba del modelo depredador-presa para diferentes coeficientes de reacción</div> | ||
| − | {| | + | <div id='tab-1'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| − | |- style=" | + | |-style="text-align:center" |
| − | + | ! !! <math>s_{11}</math> !! <math>s_{12}</math> !! <math>s_{21}</math> !! <math>s_{22}</math> | |
| − | + | |- style="text-align:center" | |
| − | + | | Caso 1 | |
| − | + | | 0 | |
| − | + | | 0 | |
| − | |- style=" | + | | 0 |
| − | | | + | | 0 |
| − | | | + | |- style="text-align:center" |
| − | | | + | | Caso 2 |
| − | | | + | | 0 |
| − | | | + | | 0 |
| − | |- style=" | + | | 0 |
| − | | | + | | 1 |
| − | | | + | |- style="text-align:center" |
| − | | | + | | Caso 3 |
| − | | | + | | 0 |
| − | | | + | | 0 |
| − | |- style=" | + | | 3 |
| − | | | + | | 0.1 |
| − | | | + | |- style="text-align:center" |
| − | | | + | | Caso 4 |
| − | | | + | | 1 |
| − | | | + | | 0 |
| − | |- style=" | + | | 3 |
| − | | | + | | 0.1 |
| − | | | + | |- style="text-align:center" |
| − | | | + | | Caso 5 |
| − | | | + | | 1 |
| − | | | + | | 2 |
| − | |- style=" | + | | 3 |
| − | | | + | | 0.1 |
| − | | | + | |
| − | | | + | |
| − | | | + | |
| − | | | + | |
| − | + | ||
|} | |} | ||
| + | |||
La malla de elementos finitos usada es regular y consta de <math display="inline">50 \times 50</math> elementos cuadrados de 4 nodos, es decir <math display="inline">\delta x=\delta y=0.02</math>, con un total de 2500 elementos y 2601 nodos. El intervalo de tiempo es <math display="inline">\left[0,1\right]</math> y el tamaño del paso de tiempo tomado es uniforme, con <math display="inline">\delta t=0.2</math>. Hemos usado el integrador temporal BDF2 y el método variacional multiescala ASGS descrito anteriormente. Presentamos resultados numéricos en diferentes instantes de tiempos de simulación, <math display="inline">t=0.2,</math> <math display="inline">0.4</math>, <math display="inline">0.6,</math> <math display="inline">0.8</math>, <math display="inline">1.0</math>, para todos los casos de prueba. | La malla de elementos finitos usada es regular y consta de <math display="inline">50 \times 50</math> elementos cuadrados de 4 nodos, es decir <math display="inline">\delta x=\delta y=0.02</math>, con un total de 2500 elementos y 2601 nodos. El intervalo de tiempo es <math display="inline">\left[0,1\right]</math> y el tamaño del paso de tiempo tomado es uniforme, con <math display="inline">\delta t=0.2</math>. Hemos usado el integrador temporal BDF2 y el método variacional multiescala ASGS descrito anteriormente. Presentamos resultados numéricos en diferentes instantes de tiempos de simulación, <math display="inline">t=0.2,</math> <math display="inline">0.4</math>, <math display="inline">0.6,</math> <math display="inline">0.8</math>, <math display="inline">1.0</math>, para todos los casos de prueba. | ||
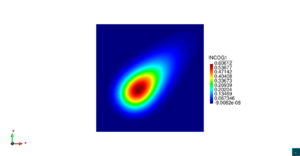
| − | En las Figuras [[#img-11|11]], [[#img-12|12]], [[#img-13|13]], [[#img-14|14]] y [[#img-15|15]] se encuentran los resultados de los casos 1, 2, 3, 4 y 5, respectivamente, considerados en la | + | En las Figuras [[#img-11|11]], [[#img-12|12]], [[#img-13|13]], [[#img-14|14]] y [[#img-15|15]] se encuentran los resultados de los casos 1, 2, 3, 4 y 5, respectivamente, considerados en la [[#table-3|Tabla 3]]. Los resultados numéricos en todos los casos son los esperados y corresponden con la realidad física de cada caso, observando además que son coincidentes con los resultados mostrados en <span id='citeF-33'></span>[[#cite-33|[33]]]. |
Las diferencias de los resultados de las densidades de población del depredador y de la presa con elementos de alto orden <math display="inline">Q_{2}</math> (con 10201 nodos), <math display="inline">Q_{3}</math> (con 22801 nodos) y <math display="inline">Q_{4}</math> (con 40401 nodos) están en el orden de las milésimas con respecto a los resultados con elementos lineales para <math display="inline">t=1.0</math>, tal como observamos en las Tablas [[#table-4|4]] y [[#table-5|5]], por lo que dependiendo de la escala del problema es suficiente la precisión con elementos lineales. | Las diferencias de los resultados de las densidades de población del depredador y de la presa con elementos de alto orden <math display="inline">Q_{2}</math> (con 10201 nodos), <math display="inline">Q_{3}</math> (con 22801 nodos) y <math display="inline">Q_{4}</math> (con 40401 nodos) están en el orden de las milésimas con respecto a los resultados con elementos lineales para <math display="inline">t=1.0</math>, tal como observamos en las Tablas [[#table-4|4]] y [[#table-5|5]], por lo que dependiendo de la escala del problema es suficiente la precisión con elementos lineales. | ||
| Line 1,101: | Line 1,083: | ||
| [[Image:Draft_Codina_913592092-test-Presa_1_0.png|300px|"Caso-1/Presa_1_0".png]] | | [[Image:Draft_Codina_913592092-test-Presa_1_0.png|300px|"Caso-1/Presa_1_0".png]] | ||
| [[Image:Draft_Codina_913592092-test-Depredador_1_0.png|300px|"Caso-1/Depredador_1_0".png]] | | [[Image:Draft_Codina_913592092-test-Depredador_1_0.png|300px|"Caso-1/Depredador_1_0".png]] | ||
| − | |||
|} | |} | ||
| − | |||
|- | |- | ||
| − | |||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="3" style="padding-bottom:10px;"| '''Figura 11'''. Caso 1. Densidad de población de la presa (izquierda). Densidad de población del depredador (derecha) |
|} | |} | ||
| Line 1,135: | Line 1,114: | ||
| [[Image:Draft_Codina_913592092-test-Presa_1_0-dup1.png|300px|"Caso-2/Presa_1_0".png]] | | [[Image:Draft_Codina_913592092-test-Presa_1_0-dup1.png|300px|"Caso-2/Presa_1_0".png]] | ||
| [[Image:Draft_Codina_913592092-test-Depredador_1_0-dup1.png|300px|"Caso-2/Depredador_1_0".png]] | | [[Image:Draft_Codina_913592092-test-Depredador_1_0-dup1.png|300px|"Caso-2/Depredador_1_0".png]] | ||
| − | |||
|} | |} | ||
| − | |||
|- | |- | ||
| − | |||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="3" style="padding-bottom:10px;"| '''Figura 12'''. Caso 2. Densidad de población de la presa (izquierda). Densidad de población del depredador (derecha) |
|} | |} | ||
| Line 1,169: | Line 1,145: | ||
| [[Image:Draft_Codina_913592092-test-Caso3_presa_1_0.png|300px|"Caso-3/Caso3_presa_1_0".png]] | | [[Image:Draft_Codina_913592092-test-Caso3_presa_1_0.png|300px|"Caso-3/Caso3_presa_1_0".png]] | ||
| [[Image:Draft_Codina_913592092-test-Caso3_depredador_1_0.png|300px|"Caso-3/Caso3_depredador_1_0".png]] | | [[Image:Draft_Codina_913592092-test-Caso3_depredador_1_0.png|300px|"Caso-3/Caso3_depredador_1_0".png]] | ||
| − | |||
|} | |} | ||
| − | |||
|- | |- | ||
| − | |||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="3" style="padding-bottom:10px;"| '''Figura 13'''. Caso 3. Densidad de población de la presa (izquierda). Densidad de población del depredador (derecha) |
|} | |} | ||
| Line 1,203: | Line 1,176: | ||
| [[Image:Draft_Codina_913592092-test-Caso4_presa_1_0.png|300px|"Caso-4/Caso4_presa_1_0".png]] | | [[Image:Draft_Codina_913592092-test-Caso4_presa_1_0.png|300px|"Caso-4/Caso4_presa_1_0".png]] | ||
| [[Image:Draft_Codina_913592092-test-Caso4_depredador_1_0.png|300px|"Caso-4/Caso4_depredador_1_0".png]] | | [[Image:Draft_Codina_913592092-test-Caso4_depredador_1_0.png|300px|"Caso-4/Caso4_depredador_1_0".png]] | ||
| − | |||
|} | |} | ||
| − | |||
|- | |- | ||
| − | |||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="3" style="padding-bottom:10px;"| '''Figura 14'''. Caso 4. Densidad de población de la presa (izquierda). Densidad de población del depredador (derecha) |
|} | |} | ||
| Line 1,237: | Line 1,207: | ||
| [[Image:Draft_Codina_913592092-test-Caso5_presa_1_0.png|300px|"Caso-5/Caso5_presa_1_0".png]] | | [[Image:Draft_Codina_913592092-test-Caso5_presa_1_0.png|300px|"Caso-5/Caso5_presa_1_0".png]] | ||
| [[Image:Draft_Codina_913592092-test-Caso5_depredador_1_0.png|300px|"Caso-5/Caso5_depredador_1_0".png]] | | [[Image:Draft_Codina_913592092-test-Caso5_depredador_1_0.png|300px|"Caso-5/Caso5_depredador_1_0".png]] | ||
| − | |||
|} | |} | ||
| − | |||
|- | |- | ||
| − | |||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="3" style="padding-bottom:10px;"| '''Figura 15'''. Caso 5. Densidad de población de la presa (izquierda). Densidad de población del depredador (derecha) |
|} | |} | ||
| − | + | <div class="center" style="font-size: 75%;">'''Tabla 4'''. Densidad de población de la presa (<math>\varphi _{1}</math>)</div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | <div id='tab-1'></div> | ||
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! !! Caso 1 !! Caso 2 !! Caso 3 !! Caso 4 !! Caso 5 | ||
| + | |- style="text-align:center" | ||
| + | | <math display="inline">Q_{1}</math> | ||
| + | | 0.48614 | ||
| + | | 0.48614 | ||
| + | | 0.48614 | ||
| + | | 0.69991 | ||
| + | | 0.56545 | ||
| + | |- style="text-align:center" | ||
| + | | <math display="inline">Q_{2}</math> | ||
| + | | 0.48847 | ||
| + | | 0.48847 | ||
| + | | 0.48847 | ||
| + | | 0.70560 | ||
| + | | 0.56853 | ||
| + | |- style="text-align:center" | ||
| + | | <math display="inline">Q_{3}</math> | ||
| + | | 0.48847 | ||
| + | | 0.48847 | ||
| + | | 0.48847 | ||
| + | | 0.70709 | ||
| + | | 0.56928 | ||
| + | |- style="text-align:center" | ||
| + | | <math display="inline">Q_{4}</math> | ||
| + | | 0.48848 | ||
| + | | 0.48848 | ||
| + | | 0.48848 | ||
| + | | 0.70786 | ||
| + | | 0.56982 | ||
|} | |} | ||
| − | + | <div class="center" style="font-size: 75%;">'''Tabla 5'''. Densidad de población del depredador (<math>\varphi _{2}</math>))</div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | <div id='tab-1'></div> | ||
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! !! Caso 1 !! Caso 2 !! Caso 3 !! Caso 4 !! Caso 5 | ||
| + | |- style="text-align:center" | ||
| + | | <math display="inline">Q_{1}</math> | ||
| + | | 0.48614 | ||
| + | | 0.22615 | ||
| + | | 0.63921 | ||
| + | | 0.70337 | ||
| + | | 0.65541 | ||
| + | |- style="text-align:center" | ||
| + | | <math display="inline">Q_{2}</math> | ||
| + | | 0.48847 | ||
| + | | 0.22685 | ||
| + | | 0.63872 | ||
| + | | 0.71223 | ||
| + | | 0.66228 | ||
| + | |- style="text-align:center" | ||
| + | | <math display="inline">Q_{3}</math> | ||
| + | | 0.48847 | ||
| + | | 0.22684 | ||
| + | | 0.63954 | ||
| + | | 0.71348 | ||
| + | | 0.66352 | ||
| + | |- style="text-align:center" | ||
| + | | <math display="inline">Q_{4}</math> | ||
| + | | 0.48848 | ||
| + | | 0.22684 | ||
| + | | 0.64002 | ||
| + | | 0.71412 | ||
| + | | 0.66422 | ||
|} | |} | ||
| − | ==5 Conclusiones== | + | ==5. Conclusiones== |
En este artículo se ha presentado la aproximación del modelo acoplado de las ecuaciones del movimiento de un fluido en aguas poco profundas junto con las ecuaciones de convección-difusión-reacción del transporte de contaminantes mediante formulaciones estabilizadas de elementos finitos de alto orden (hasta el cuarto orden). | En este artículo se ha presentado la aproximación del modelo acoplado de las ecuaciones del movimiento de un fluido en aguas poco profundas junto con las ecuaciones de convección-difusión-reacción del transporte de contaminantes mediante formulaciones estabilizadas de elementos finitos de alto orden (hasta el cuarto orden). | ||
| Line 1,348: | Line 1,307: | ||
R. Codina agradece la ayuda recibida a través del programa ICREA Academia, del Gobierno de Catalunya. | R. Codina agradece la ayuda recibida a través del programa ICREA Academia, del Gobierno de Catalunya. | ||
| − | === | + | ==Referencias== |
| + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | ||
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[1]]] Zlatev Z. The air pollution problem. In: Computer Treatment of Large Air Pollution Models, Environmental Science and Technology Library, vol 2, Springer, Dordrecht, 1995. | |
<div id="cite-2"></div> | <div id="cite-2"></div> | ||
| − | + | [[#citeF-2|[2]]] Zienkiewicz O.C., Taylor R.L. The Finite element method. Fluid Mechanics. Butterworth- Heinemann, vol. 3, 5th edition, 2000. | |
<div id="cite-3"></div> | <div id="cite-3"></div> | ||
| − | + | [[#citeF-3|[3]]] Li S., Duffy C.J. Fully-coupled modeling of shallow water flow and pollutant transport on unstructured grids. Procedia Environmental Sciences, 13:20982121, 2012. | |
<div id="cite-4"></div> | <div id="cite-4"></div> | ||
| − | + | [[#citeF-4|[4]]] Behzadi F., Newman III J.C. A Semi-discrete SUPG method for contaminant transport in shallow water models. Procedia Computer Science, 80:1313-1323, 2016. | |
<div id="cite-5"></div> | <div id="cite-5"></div> | ||
| − | + | [[#citeF-5|[5]]] Benkhaldoun F., Elmahi I., Seaïd M. Well-balanced finite volume schemes for pollutant transport by shallow water equations on unstructured meshes. J. Comput. Phys., 1:180-203, 2007. | |
<div id="cite-6"></div> | <div id="cite-6"></div> | ||
| − | + | [[#citeF-6|[6]]] Komatsu T., Ohgushi A.K., Asai K. Refined numerical scheme for advective transport in diffusion simulation. J. Hydraul. Eng., 123:41-50, 1997. | |
<div id="cite-7"></div> | <div id="cite-7"></div> | ||
| − | + | [[#citeF-7|[7]]] Begnudelli L., Sanders B.F. Unstructured grid finite-volume algorithm for shallow-water flow and scalar transport with wetting and drying. Journal of Hydraulic Engineering, 132(4):371-384, 2006. | |
<div id="cite-8"></div> | <div id="cite-8"></div> | ||
| − | + | [[#citeF-8|[8]]] Cea L., Vázquez-Cedón M.E. Unstructured finite volume discretisation of bed friction and convective flux in solute transport models linked to the sallow water equations. Journal of Computational Physics, 231(8):3317-3330, 2012. | |
<div id="cite-9"></div> | <div id="cite-9"></div> | ||
| − | + | [[#citeF-9|[9]]] Caleffi V., Valiani A. A 2D local discontinuous Galerkin method for contaminant transport in channel bends. Computers & Fluids, 88:629-642, 2013. | |
<div id="cite-10"></div> | <div id="cite-10"></div> | ||
| − | + | [[#citeF-10|[10]]] Pavan S., Hervouet J.M., Ricchiuto M., Ata R. A second order residual based predictorcorrector approach for time dependent pollutant transport. Journal of Computational Physics, 318:122141, 2016. | |
<div id="cite-11"></div> | <div id="cite-11"></div> | ||
| − | + | [[#citeF-11|[11]]] Cai L., Xie W.-X., Feng J.-H., Zhou J. Computations of transport of pollutant in shallow water. Applied Mathematical Modelling, 31:490498, 2007. | |
<div id="cite-12"></div> | <div id="cite-12"></div> | ||
| − | + | [[#citeF-12|[12]]] Postma L., Hervouet J.-M. Compatibility between finite volumes and finite elements using solutions of shallow water equations for substance transport. Int. J. Numer. Methods Fluids, 53(9):14951507, 2007. | |
<div id="cite-13"></div> | <div id="cite-13"></div> | ||
| − | + | [[#citeF-13|[13]]] Pavan S., Ata R., Hervouet J.-M. Finite volume schemes and residual distribution schemes for pollutant transport on unstructured grids. Environ. Earth Sci., 74:73377356, 2015. | |
<div id="cite-14"></div> | <div id="cite-14"></div> | ||
| − | + | [[#citeF-14|[14]]] Liu H., Zhou J.G., Li M., Zhao Y. Multi-block lattice Boltzmann simulations of solute transport in shallow water flows. Advances in Water Resources, 58:24-40, 2013. | |
<div id="cite-15"></div> | <div id="cite-15"></div> | ||
| − | + | [[#citeF-15|[15]]] Hammou H., Ginzburg I., Boulerhcha M. Two-relaxation-times lattice Boltzmann schemes for solute transport in unsaturated water flow with a focus on stability. Adv Wat Res., 4(6):779-793, 2011. | |
<div id="cite-16"></div> | <div id="cite-16"></div> | ||
| − | + | [[#citeF-16|[16]]] Zhou J.G. A lattice Boltzmann method for solute transport. Int J Numer Methods Fluids, 61:848-63, 2009. | |
<div id="cite-17"></div> | <div id="cite-17"></div> | ||
| − | + | [[#citeF-17|[17]]] Codina R., Badia S., Baiges J., Principe J. Variational multiscale methods in computational fluid dynamics. In: Encyclopedia of Computational Mechanics, E. Stein, R. Borst and T.J.R. Hughes (eds.), doi: [https://onlinelibrary.wiley.com/doi/abs/10.1002/9781119176817.ecm2117 10.1002/9781119176817.ecm21172017], 2017. | |
<div id="cite-18"></div> | <div id="cite-18"></div> | ||
| − | + | [[#citeF-18|[18]]] Rogers B., Fujihara M., Borthwick A.G.L. Adaptive Q-tree Godunov-type scheme for shallow water equations. Int J Numer Methods Fluids, 35:247-80, 2001. | |
<div id="cite-19"></div> | <div id="cite-19"></div> | ||
| − | + | [[#citeF-19|[19]]] H. Yamamoto. Lecture 8: The shallow-water equations. June 2009, 9pp. https://www.coursehero.com/file/35480149/othersonline-HW4pdf/ | |
| − | + | ||
| − | https://www.coursehero.com/file/35480149/othersonline-HW4pdf/ | + | |
<div id="cite-20"></div> | <div id="cite-20"></div> | ||
| − | + | [[#citeF-20|[20]]] Hughes T.J.R. Multiscale phenomena: Green's functions, the Drichlet-to-Neumann formulation, subgrid scale models, bubbles and the origins of stabilized methods. Computer Methods in Applied Mechanics and Engineering, 127(1-4):387-401, 1995. | |
<div id="cite-21"></div> | <div id="cite-21"></div> | ||
| − | + | [[#citeF-21|[21]]] Hughes T.J.R., Feijóo G.O., Mazzei L., Quincy J.B.. The variational multiscale method-a paradign for computational mechanics. Computer Methods in Applied Mechanics and Egineering, 166:3-24, 1998. | |
<div id="cite-22"></div> | <div id="cite-22"></div> | ||
| − | + | [[#citeF-22|[22]]] Codina R. On stabilized finite element methods for linear systems of convection-diffusion-reaction equations. Computer Methods in Applied Mechanics and Engineering, 188:61-82, 2000. | |
<div id="cite-23"></div> | <div id="cite-23"></div> | ||
| − | + | [[#citeF-23|[23]]] Codina R. A stabilized finite element method for generalized stationary incompressible flows. Computer Methods in Applied Mechanics and Enginineering, 190:2681-2706, 2001. | |
<div id="cite-24"></div> | <div id="cite-24"></div> | ||
| − | + | [[#citeF-24|[24]]] Codina R. Comparison of some finite element methods for solving the diffusion-convection-reaction equation. Computer Methods in Applied Mechanics and Engineering, 156:185-210, 1998. | |
<div id="cite-25"></div> | <div id="cite-25"></div> | ||
| − | + | [[#citeF-25|[25]]] Codina R., Blasco J. Analysis of a stabilized finite element approximation of the transient convection-diffusion-reaction equation using orthogonal subscales. Computing and Visualization in Science, 4:167-174, 2002. | |
<div id="cite-26"></div> | <div id="cite-26"></div> | ||
| − | + | [[#citeF-26|[26]]] Codina R. Stabilized finite element approximation of transient incompressible flows using orthogonal subscales. Computer Methods in Applied Mechanics and Engineering, 191:4295-4321, 2002. | |
<div id="cite-27"></div> | <div id="cite-27"></div> | ||
| − | + | [[#citeF-27|[27]]] Villota A., Codina R. Approximation of the shallow water equations with higher order finite elements and variational multiscale methods. Rev. int. métodos numér. cálc. diseño ing., 34(1), 28, 2018. URL https://www.scipedia.com/public/Villota_Codina_a. | |
<div id="cite-28"></div> | <div id="cite-28"></div> | ||
| − | + | [[#citeF-28|[28]]] Codina R. Finite element approximation of the convection-diffusion equation: subgrid-scale spaces, local instabilities and anisotropic space-time discretizations. In Bail 2010 - Boundary and Interior Layers, Computational and Asymptotic Methods, Lecture Notes in Computational Science and Engineering, C. Clavero, J.L. Gracia and F.J. Lisbona (eds.), vol. 81, pages 85-97, Springer, 2011. | |
<div id="cite-29"></div> | <div id="cite-29"></div> | ||
| − | + | [[#citeF-29|[29]]] Codina R., González-Ondina J.M., Díaz-Hernández G., Principe J. Finite element approximation of the modified Boussinesq equations using a stabilized formulation, International Journal for Numerical Methods in Fluids, 57:1249-1268, 2008. | |
<div id="cite-30"></div> | <div id="cite-30"></div> | ||
| − | + | [[#citeF-30|[30]]] Villota A., Codina R. Approximation of the scalar convection-diffusion-reaction equation with stabilized finite element formulations of high order. Rev. int. métodos numér. cálc. diseño ing., 35(1), 6, 2019. URL https://www.scipedia.com/public/Villota_Codina_a | |
<div id="cite-31"></div> | <div id="cite-31"></div> | ||
| − | + | [[#citeF-31|[31]]] Principe J., Codina R. On the stabilization parameter in the subgrid scale approximation of scalar convection-diffusion-reaction equations on distorted meshes. Computer Methods in Applied Mechanics and Engineering, 199:1386-1402, 2010. | |
<div id="cite-32"></div> | <div id="cite-32"></div> | ||
| − | + | [[#citeF-32|[32]]] Codina R. On hp convergence of stabilized finite element approximations of the convection-diffusion equation. SeMA Journal, 75:591-606, 2018. | |
<div id="cite-33"></div> | <div id="cite-33"></div> | ||
| − | + | [[#citeF-33|[33]]] Sheshachala S.K., Codina R. Finite element modeling of nonlinear reaction-diffusion-advection systems of equations. International Journal of Numerical Methods for Heat & Fluid Flow, 28(11):2688-2715, 2018. https://doi.org/10.1108/HFF-02-2018-0077 | |
| + | </div> | ||
Latest revision as of 14:46, 27 October 2020
Resumen
En este artículo presentamos la aproximación del modelo acoplado de las ecuaciones del movimiento de un fluido en aguas poco profundas con la ecuación convección-difusión-reacción (CDR) del transporte de contaminantes. Dicha aproximación se realiza mediante elementos finitos de alto orden y usando métodos variacionales estabilizados de subescalas. El sistema acoplado de ecuaciones, previamente discretizado en el tiempo y linealizado, lo escribimos como una ecuación vectorial transitoria de CDR. Los métodos estabilizados de elementos finitos utilizados son los conocidos métodos de subescalas ASGS y OSS, los mismos que nos permiten usar igual interpolación para todas las incógnitas, así como tratar con flujos de convección y reacción dominantes. Consideramos la posibilidad de no linealidad tanto en el término convectivo como en el de reacción. No consideraremos el posible desarrollo de choques en la solución. Con el fin de examinar la precisión y robustez de los métodos ASGS y OSS, presentamos cuatro casos de prueba: convergencia en malla, transporte de un contaminante en una cavidad cuadrada, transporte de un contaminante en el golfo de Roses y en la desembocadura del río Guadalquivir, y el modelo depredador-presa, que puede escribirse como una ecuación vectorial de CDR transitoria con no linealidad en el término de reacción.
Palabras clave: Aguas poco profundas, ablandamiento y estabilización, transporte de contaminantes, modelo depredador-presa
Abstract
In this article we present the approximation of the coupled model of the equations of motion of a fluid in shallow waters with the convection-diffusion-reaction (CDR) equation of pollutant transport. This approximation is carried out using high order finite elements and using stabilised variational sub-scale methods. We write the coupled system of equations, previously discretised in time and linearised, as a transient vector equation of CDR. The stabilised finite element methods used are the known ASGS and OSS sub-scale methods, the same ones that allow us to use the same interpolation for all unknowns, as well as to deal with dominant convection and reaction flows. We consider the possibility of non-linearity in both the convective and reaction terms. We will not consider the possible development of shocks in the solution. In order to examine the accuracy and robustness of the ASGS and OSS methods, we present four test cases: mesh convergence, transport of a pollutant in a square cavity, transport of a pollutant in the Gulf of Roses and at the river Guadalquivir mouth, and the predator-prey model, which can be written as a transient CDR vector equation with non-linearity in the reaction term.
Keywords: Shallow waters, softening and stabilization, transport of pollutants, predator-prey model
1. Introducción
Un contaminante es aquel componente que está presente en el agua a niveles perjudiciales para la vida de los seres humanos, plantas y animales ([1], véase también los informes de la U.S. Environmental Protecction Agency, https://www.epa.gov/). La simulación del transporte de contaminantes para la predicción de la concentración de contaminantes en ríos, lagos, lagunas y regiones costeras tiene importancia estratégica en el análisis y diseño de soluciones de los problemas de contaminación ambiental del planeta.
En el fenómeno físico del movimiento de contaminantes se deben distinguir tres procesos: la difusión, la convección y la reacción. La difusión es el proceso físico debido al cual el contaminante se mueve como resultado del movimiento intermolecular de las partículas de ambas sustancias, el fluido que la transporta (agua) y el contaminante. La convección es el movimiento del soluto (contaminante) debido al movimiento del agua, por lo cual si el agua permanece en reposo no hay convección. Finalmente, la reacción tiene en cuenta el posible efecto de crecimiento o decrecimiento de un contaminante por factores externos (calor, especies con las que puede combinarse); en el caso de haber distintas especies de contaminantes, la reacción puede modelar la interacción entre ellas.
La formulación del problema del transporte de contaminantes se fundamenta, como la de todos los fenómenos físicos, en las ecuaciones de equilibrio y las ecuaciones constitutivas. Las ecuaciones del transporte de sustancias disueltas o en suspensión en el flujo se basan en el principio de conservación de la masa de dichas sustancias en caso de que no haya reacción o en el modelo de crecimiento o decrecimiento en caso de que la haya. En el problema que queremos abordar, la dinámica del transporte de contaminantes involucra los modelos de flujos del campo de velocidades en aguas someras y del transporte, difusión y reacción de contaminantes, los cuales tienen características de la ecuación transitoria de convección, difusión y reacción (CDR).
En este trabajo vamos a utilizar un modelo matemático que acopla las ecuaciones del movimiento de un fluido en aguas poco profundas con la ecuación de CDR del transporte de contaminantes. Las ecuaciones del movimiento de un fluido en aguas poco profundas que vamos a utilizar son las obtenidas a partir de las ecuaciones de Navier-Stokes para fluidos viscosos, y que se encuentran descritas por ejemplo en [2], acopladas a la ecuación de CDR del transporte de contaminantes como en [3,4,5], entre otras referencias. El sistema acoplado de ecuaciones se puede escribir en forma conservativa en términos de la profundidad del fluido, de las velocidades y de las concentraciones de contaminantes promediadas en el plano donde el flujo medio tiene lugar. La presencia del término fuente en la ecuación de momento, la consideración de la batimetría variable, la fricción en el fondo del lecho, la tensión en la superficie libre del agua debida al viento y el efecto de Coriolis son características que se pueden tomar en cuenta para obtener modelos físicos más realistas del flujo de aguas someras. El resultado es un sistema no lineal acoplado de ecuaciones diferenciales parciales. Para simplificar el modelo, supondremos que los contaminantes son pasivos, en el sentido de que no afectan la densidad del fluido y por lo tanto el flujo; en caso de no ser así, se podría introducir fácilmente algún modelo de flotación que tuviera en cuenta el flujo generado por la variabilidad en la concentración de contaminantes.
En la literatura existe mucha investigación numérica en el área del transporte de contaminantes en aguas poco profundas, aplicando métodos de diferencias finitas [6], métodos de volúmenes finitos [7,8,11,12,13], métodos de elementos finitos [4,9,10], métodos tipo-Godunov [18] y métodos de Boltzmann [14,15,16].
En este trabajo vamos a realizar la aproximación de las ecuaciones del movimiento de un fluido en aguas poco profundas acopladas a la ecuación de CDR del transporte de contaminantes mediante los métodos VMS (Variational Muli-Scale) llamados ASGS (Algebraic SubGrid Scale) y OSS (Orthogonal Subgrid Scale) (véase [17]). El propósito de este trabajo es tanto aplicar estas técnicas, ya conocidas, a problemas no lineales como el transporte de contaminantes en aguas poco profundas y el modelo depredador-presa, como experimentar con elementos finitos de orden elevado (hasta el cuarto orden).
Veremos en primer lugar que mediante un cambio de variables apropiado y linealizando el sistema acoplado de ecuaciones en aguas poco profundas con las ecuaciones del transporte de contaminantes, cada iteración del proceso no lineal puede escribirse como una ecuación vectorial de CDR transitoria lineal. Plantearemos la aproximación en el tiempo y el espacio de esta ecuación vectorial de CDR transitoria, para luego particularizarla al sistema acoplado de las ecuaciones del flujo en aguas poco profundas con el transporte de contaminantes.
En lo concerniente a la discretización, primero procederemos a discretizar en el tiempo mediante un esquema de integración temporal en diferencias finitas y luego realizaremos la aproximación en el espacio mediante elementos finitos, aunque el enfoque más común es proceder a la inversa, es decir, primero discretizar en el espacio y luego aproximar el sistema resultante de ecuaciones diferenciales en el tiempo. Sin embargo, el enfoque de discretizar primero en el tiempo nos permite desacoplar los errores provenientes de la discretización temporal de los correspondientes a la discretización espacial. Aunque ambos caminos para el método estandar de Galerkin dan el mismo problema discreto, esto no es así para todos los métodos basados en VMS. En lo referente a la discretización temporal, usaremos la regla trapezoidal generalizada, que es el método en diferencias finitas más sencillo; sin embargo, cualquier otro método en diferencias finitas o incluso en elementos finitos podría aplicarse. En particular, en los ejemplos numéricos usamos esquemas de integración temporal de mayor orden que la regla trapezoidal.
En cuanto a la discretización espacial, es bien conocido que el método estándar de Galerkin presenta inestabilidades numéricas cuando los términos convectivo o de reacción son dominantes con respecto al término difusivo, además de por la necesidad dada por la condición inf-sup de usar diferentes interpolaciones de elementos finitos para la profundidad, las velocidades promediadas y la concentración de contaminante. Estos dos inconvenientes pueden superarse utilizando una formulación estabilizada. Aquí vamos a usar las formulaciones basadas en subescalas introducidas por Hughes y otros en [20,21] para la ecuación CDR escalar estacionaria y generalizado a sistemas lineales estacionarios en [22,23], y a sistemas lineales transitorios en [24,25,26], dando lugar a las formulaciones ASGS y OSS para resolver el problema de CDR vectorial transitorio, como en [27]. La idea básica es aproximar el efecto de la componente de la solución continua que no puede ser resuelta por la malla de elementos finitos en términos de la solución en el espacio de elementos finitos (método ASGS), o en términos de una subescala ortogonal respecto del producto escalar de al espacio de elementos finitos [28,29] (método OSS). Hay que hacer notar que no consideraremos el posible desarrollo de choques en la solución, es decir, discontinuidades que pueden llegar a producirse en el límite invíscido. Para tomar en cuenta esto es necesario desarrollar técnicas de captura de discontinuidades que no consideraremos en este trabajo, así como tampoco el tratamiento de subescalas dinámicas.
El artículo está organizado como sigue. En la siguiente sección se describe la física del problema a ser resuelto y la obtención de la ecuación vectorial de CDR transitoria que representa el problema acoplado de las ecuaciones del movimiento de un fluido en aguas poco profundas con las ecuaciones del transporte de contaminantes. Las aproximaciones y formulaciones de los métodos variacionales estabilizados ASGS y OSS para la ecuación vectorial de CDR transitoria están descritos en la sección 3. En la sección 4 se presentan pruebas numéricas de convergencia en malla con soluciones analíticas conocidas, un ejemplo clásico de la literatura del transporte de un contaminante en una cavidad cuadrada, dos ejemplos prácticos del transporte de un contaminante, uno en el golfo de Roses y otro en la desembocadura del río Guadalquivir, y un ejemplo del modelo depredador-presa. Finalmente, en base a los resultados obtenidos, en la Sección 5 se detallan algunas conclusiones.
2. Planteamiento del problema del transporte de contaminantes
2.1 Ecuaciones de gobierno
Las ecuaciones del movimiento de un fluido en aguas poco profundas se obtienen por integración vertical de las ecuaciones del movimiento, bien sea de fluidos viscosos (ecuaciones de Navier-Stokes) o invíscidos (ecuaciones de Euler); véase por ejemplo [2,19]. En este trabajo vamos a utilizar las ecuaciones obtenidas a partir de las ecuaciones de Navier-Stokes para un fluido Newtoniano incompresible e isotérmico, incluyendo la tensión superficial provocada por los efectos del viento así como también los efectos de Coriolis, al igual que batimetría variable, fricción en el fondo del lecho y distribución hidrostática de presiones. Vamos a considerar el problema de mecánica de fluidos acoplado con el de transporte de contaminantes. Esta será en esencia la diferencia del presente trabajo con respecto a [27], por lo que muchos de los desarrollos que presentamos aquí se encuentran también en esta referencia. Omitiremos aquellos desarrollos que no afectan la compresión de este artículo, aunque para permitir la lectura auto-contenida se repetirán muchos otros.
Sea un dominio acotado con coordenadas cartesianas Consideremos un fluido que se mueve durante el intervalo de tiempo en el dominio de dado por donde la coordenada representa la batimetría del terreno y , que será incógnita del problema, es la superficie libre del fluido con , . Consideraremos que es mucho menor que el diámetro de , por lo que supondremos válida la aproximación de las ecuaciones de movimiento en aguas poco profundas. Dichas ecuaciones acopladas a la ecuación del transporte de contaminantes pueden escribirse en forma indicial como
|
con
|
y
|
|
(6) |
donde son las componentes de la velocidad promediadas en la profundidad, es la delta de Kronecker, denota la derivada temporal y la derivada con respecto a la -ésima coordenada cartesiana en . En las ecuaciones anteriores y en lo que sigue, índices repetidos indican la notación de sumación de Einstein, y los subíndices recorren desde 1 hasta 2. En las expresiones previas, es la aceleración de la gravedad, la densidad del fluido, son las tensiones viscosas promediadas, es el coeficiente de viscosidad dinámico, es el parámetro de Coriolis, es la presión atmosférica, son las tensiones en la superficie libre del agua debidas al viento, Ch es el coeficiente de Chézy para el rozamiento en el fondo y es la norma euclídea de . Usaremos letras griegas como subíndices para caracterizar los contaminantes, cuyo número supondremos que es . Así, la concentración del contaminante promediada en la profundidad se representa por . son las componentes de la matriz de términos de reacción de la ecuación de conservación de contaminantes, con , ; en los casos de reacción no lineal, puede depender de las concentraciones de contaminantes, es decir, . es el coeficiente empírico de difusión (dispersión) para el contaminante ; nótese que por simplificar hemos supuesto que la dispersión del contaminante no se ve afectada por el resto de contaminantes, aunque esta situación podríamos incluirla fácilmente.
Las ecuaciones (1), (2) y (3) representan un sistema de ecuaciones, cuyo vector de incógnitas es
|
|
Dichas ecuaciones constituyen el modelo acoplado del movimiento de un fluido en aguas poco profundas y el transporte de contaminantes. Las mismas se deben completar con las condiciones iniciales y de contorno. Los valores iniciales para la elevación del agua, las velocidades promediadas y la concentración del contaminante deben ser conocidos como condiciones iniciales. Con respecto a las condiciones de contorno, es bien conocido que el problema está bien puesto si la velocidad promediada se especifica en el contorno de entrada del dominio computacional , mientras que en el resto del contorno se prescribe la componente normal de las tensiones viscosas y la elevación del fluido. Para las concentraciones de contaminantes, además de la condición inicial es necesario conocer como condiciones de contorno sus valores en el contorno de entrada del dominio de cálculo y los flujos en el contorno de salida; esta situación permitiría en particular considerar nulas las difusiones de contaminantes.
Debido a la complejidad del modelo descrito anteriormente, en la literatura existen muchas variantes de estas ecuaciones con distintas simplificaciones, como por ejemplo eliminar el término de difusión considerando convección pura; este es el caso de [3,4,5]. En nuestro trabajo utilizaremos las ecuaciones (1), (2) y (3) sin eliminar o hacer simplificaciones de ninguno de sus términos. Mediante un cambio de variables transformaremos las ecuaciones para poder escribirlas como una ecuación vectorial de CDR transitoria de la forma
|
|
(7) |
para la que más adelante, en la Sección 3, presentaremos su aproximación numérica por elementos finitos mediante los métodos variacionales de subescalas ASGS y OSS. En las ecuaciones anteriores, es el vector de incógnitas, el vector de fuerzas conocido y , , matrices dadas, que pueden depender de en problemas no lineales.
2.2 Cambio de variables
Realizando un cambio de variables, , y , con las ecuaciones (1), (2) y (3) se pueden escribir de la siguiente manera:
|
Las ecuaciones (8), (9) y (10) se pueden escribir fácilmente en el formato de la ecuación (7). Sin embargo esto lo haremos en el caso del problema linealizado y discretizado en el tiempo.
2.3 Discretización en el tiempo y linealización
Para la discretización temporal del modelo acoplado de las ecuaciones del movimiento de un fluido en aguas poco profundas y del transporte de contaminantes, consideremos una partición uniforme del intervalo de tiempo , con , donde es el tamaño del paso de tiempo, considerado constante. Aquí y en adelante, usaremos el superíndice para indicar el nivel de tiempo .
Aunque la discretización en el tiempo puede realizarse mediante cualquier aproximación de la derivada temporal en diferencias finitas o elementos finitos, aquí utilizaremos la regla trapezoidal generalizada. Para una función genérica , sea
|
|
(11) |
Aproximaremos
|
|
Esta aproximación es de segundo orden en en el caso en que (método de Crank-Nicolson) y de primer orden si . Para corresponde al método de Euler implícito o el método de diferencias hacia atrás de primer orden (BDF1).
En cuanto a la linealización, utilizaremos el método de punto fijo de Picard. En cada iteración de cada paso de tiempo, el problema a resolver es de la forma:
|
Usando un superíndice adicional para el contador de iteraciones, las variables introducidas en (12), (13) y (14) para la iteración -ésima en el paso de tiempo son
|
|
El super-índice es el contador de las iteraciones debidas a la no linealidad. Obsérvese que la forma linealizada de las tensiones viscosas dada en la ecuación (4) corresponde a donde está escrito en términos de las variables de la iteración actual, mientras que se calcula con los valores de las variables correspondientes a la iteración anterior. Nótese que hemos usado el símbolo para indicar las componentes de la matriz de términos reactivos provenientes de la ecuación de conservación de la cantidad de movimiento, para distinguirlas de las provenientes de la ecuación de conservación de contaminantes, aunque ambas contribuirán a la matriz de términos reactivos en la forma vectorial que presentamos a continuación.
2.4 Forma vectorial
Para escribir las ecuaciones (12), (13) y (14) en la forma vectorial (7), aunque discretizada en el tiempo, escribimos las mismas como un sistema de ecuaciones con incógnitas. Las ecuaciones correspondientes a las velocidades y altura de la lámina de agua son las mismas que en [27], mientras que la ecuación correspondiente a la concentración de los contaminantes es:
|
|
En esta ecuación hay suma para el índice , pero no para , que es el contador de contaminante considerado.
Para simplificar la notación, consideremos un único contaminante, caracterizado por el índice genérico . La forma vectorial (7) del sistema de ecuaciones final, previamente discretizadas en el tiempo y linealizadas con el método de punto fijo de Picard, está dada por:
|
|
(15) |
con
|
|
En caso de considerar contaminantes, el coeficiente 4-4 de la matriz de términos reactivos sería de hecho una matriz , con el coeficiente dado por .
La ecuación (15) corresponde a la ecuación vectorial de CDR transitoria (7) de las ecuaciones acopladas del movimiento de un fluido en aguas poco profundas y del transporte de contaminantes, discretizadas en el tiempo y linealizadas. Las matrices , y , de nuevo para el caso de un contaminante, son
|
|
Obsérvese que las matrices son simétricas. Los coeficientes de las matrices y no todos son constantes, pues algunos dependen de las velocidades del flujo, elevación del nivel del agua, su batimetría y sus gradientes, cuyos valores corresponden a la iteración anterior resultado de la linealización. Asimismo, en el caso de reacciones no lineales entre contaminantes los coeficientes pueden depender de las concentraciones de estos evaluadas en la iteración anterior del actual paso de tiempo.
En el caso de contaminantes, el vector de incógnitas es
|
|
3. Aproximación espacial y estabilización numérica
Una vez hemos conseguido escribir las ecuaciones del problema en la forma (7), el proceso es exactamente el mismo que el seguido en [27] para llevar a cabo la aproximación espacial, por lo que aquí nos centraremos solamente en el problema discreto final y la forma de tratar la ecuación de transporte de contaminantes.
La aproximación de Galerkin del problema es estándar. Dicha aproximación parte de la forma variacional del problema. Una vez discretizado el dominio de cálculo en una partición de elementos finitos de , con , siendo el número de elementos de la partición, podemos construir el espacio de elementos finitos que aproxima el espacio donde se encuentra la solución del problema continuo. El método de Galerkin consiste en tomar las funciones de test de la forma variacional en el mismo espacio.
En el problema que nos ocupa, el método de Gakerkin puede ser inestable por tres motivos. En primer lugar, la interpolación de la altura de la lámina de agua no puede ser independiente de la de la velocidad promediada: ambas interpolaciones tienen que cumplir la condición inf-sup que garantiza que el problema está bien puesto desde el punto de vista matemático. En segundo lugar, si los términos viscosos (o difusivos) son pequeños comparados con los convectivos, pueden aparecer oscilaciones en todo el dominio de cálculo, como es bien conocido. Este problema afecta tanto a las ecuaciones mecánicas, para altura de agua y velocidad promedio, como a las ecuaciones de transporte de contaminantes. Finalmente, si los términos reactivos son dominantes respecto de los difusivos, pueden aparecer también oscilaciones numéricas, esta vez localizadas cerca de los contornos y de las capas límite. Aunque este problema pudiera parecer poco importante, estas oscilaciones localizadas pueden ser muy perjudiciales en problemas no lineales como el que nos ocupa, pues pueden impedir que los esquemas iterativos converjan.
Todas las inestabilidades descritas se pueden evitar usando métodos de elementos finitos estabilizados. Como se ha dicho anteriormente, en este trabajo usaremos métodos basados en el concepto de VMS. En [17] se presenta una revisión de los mismos aplicados a problemas de mecánica de fluidos, mientras que en [27] se describe su aplicación a un problema formalmente análogo al que nos ocupa, aunque sin las ecuaciones de transporte de contaminantes.
En el problema que estamos considerando, la forma final discreta del problema a resolver es:
|
|
(16) |
Para explicar los distintos términos de este problema discreto, empecemos diciendo que se entiende que esta ecuación corresponde a un cierto paso de tiempo de la discretización temporal, aunque hemos omitido el superíndice del paso de tiempo para no cargar la notación. Asimismo, hemos visto que estas ecuaciones corresponden también a una cierta iteración del proceso iterativo resultado de la linealización del problema.
El subíndice hace referencia a funciones en el espacio de elementos finitos (que aquí nada tiene que ver con la altura de la lámina de agua)). Así, es la aproximación a la incógnita , mientras que es una función de test arbitraria, cumpliendo las adecuadas condiciones de contorno. Hemos usado el símbolo para indicar la integral sobre el dominio de cálculo del producto de dos funciones, reemplazándolo por cuando estas funciones son de cuadrado integrable, como sucede con el término temporal.
El operador es el asociado al problema (7), es decir
|
|
mientras que denota su adjunto (sin condiciones de contorno), dado por
|
La forma Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle B}
en la ecuación (16) es la asociada al problema escrito en forma débil, es decir, la del método de Galerkin. Suponiendo que las matrices Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \mathbf{A}_{i}} se descomponen en una parte que no se integra por partes, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \mathbf{A}^c_{i}}
, y otra que sí, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \mathbf{A}^f_{i}}
(y que por consiguiente contribuye a los flujos de contorno), y que las condiciones de contornos son homogéneas, para simplificar, en nuestro caso tenemos que
|
Solo nos queda por describir el término llamado de estabilización en la ecuación (16). En primer lugar, el operador Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \mathbf{P}}
define el método que estamos considerando. En el caso en que Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \mathbf{P} = \mathbf{I}}
, la identidad, nos referiremos a este método como ASGS, mientras que si Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \mathbf{P}}
es la proyección ortogonal al espacio de elementos finitos, el método resultante es el llamado OSS. Los detalles de cómo motivar dichos métodos y cómo se particularizan al problema que nos ocupa (aunque sin las concentraciones de contaminantes), pueden encontrarse en [17,27]. Solo falta describir el cálculo de la llamada matriz de parámetros de estabilización Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \boldsymbol{\tau }^{e}}
, calculada en cada elemento Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle e}
de la partición de elementos finitos. Tomaremos dicha matriz como diagonal, de la forma
|
(17) |
con
|
donde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle c_{1},}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle c_{2},}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle c_{3}}
y Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle c_{4}}
son parámetros numéricos, y que para los ejemplos numéricos hemos adoptado Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle c_{1}=12,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle c_{2}=2}
y Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle c_{3}=c_{4}=1}
. En estas expresiones, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \nu _{H}=\frac{\mu _{H}}{\rho }}
es el coeficiente de viscosidad cinemática, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle |\boldsymbol{a}|}
es la norma de la velocidad y Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle d}
es el orden polinomial de interpolación.
La justificación de los parámetros de estabilización usados, así como algunas técnicas numéricas que hemos empleado en elementos de alto orden, puede consultarse en [17,30] (véase también [31,32]).
4. Resultados de los experimentos numéricos
Con el propósito de evaluar las formulaciones de los métodos variacionales de subescalas ASGS y OSS con elementos finitos de alto orden en la ecuación vectorial de CDR transitoria, con no linealidad en los términos convectivo y de reacción, hemos realizado diferentes experimentos numéricos, tales como pruebas de convergencia en malla para el problema del transporte de un contaminante, la aproximación de un ejemplo numérico del transporte de un contaminante en una cavidad cuadrada que se encuentra en la literatura, un ejemplo práctico de distribución del transporte de un contaminante en el golfo de Roses y en la desembocadura del río Guadalquivir, y un ejemplo del modelo depredador-presa.
El método de linealización utilizado es el de Picard. El criterio de convergencia para la no linealidad se ha fijado en la norma Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle L^{2},}
es decir, el proceso iterativo se considera convergido cuando
|
donde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle i}
es el contador de iteraciones en un paso de tiempo dado y Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle tol}
es la tolerancia de convergencia, fijada en Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle 10^{-5}}
en todos los ejemplos. Aquí y en lo que sigue, las normas Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle L^{2}}
se extienden a todo el dominio Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \Omega{.}}
En los casos del transporte de contaminantes estudiaremos el transporte de un solo contaminante, excepto en el ejemplo del modelo depredador-presa.
4.1 Pruebas de convergencia en malla
Las pruebas de convergencia en malla para el problema del transporte de un contaminante que hemos realizado consisten en calcular el error en norma Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle L^{2}}
entre el valor exacto de una solución manufacturada y la aproximación numérica de una de las incógnitas del problema, el cual debe ser menor o igual que el valor teórico. Sabemos que si el error del método se comporta como el error de la interpolación, situación que puede considerarse óptima, este error debe cumplir con
|
(20) |
donde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle u_{h}}
es la aproximación de la incógnita Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle u}
en el espacio de elementos finitos, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle C}
es una constante positiva, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle h}
es el diámetro de la partición de elementos finitos (no confundir con la altura de la lámina de agua) y Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle d}
el grado polinómico de la función de forma correspondiente a la interpolación de la aproximación Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle u_{h}}
. Consideraremos pruebas de convergencia en malla para Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle 1\leq d\leq{4}} .
Si graficamos la ecuación (20) (en el caso de la igualdad) en el plano, con Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \mathrm{log}\,e}
en las ordenadas y Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \mathrm{log}\,h}
en las abscisas, tenemos una línea recta, donde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle d+1}
es la pendiente teórica óptima de convergencia. Las pruebas de convergencia en malla consisten entonces en verificar que la pendiente calculada sea precisamente Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle d+1}
. Para ello, seleccionamos como solución exacta tanto para las velocidades Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle U_1} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle U_2}
como para la elevación de la superficie libre del agua Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \eta }
y para la concentración de un contaminante Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \varphi }
, la función polinómica espacio-temporal
|
e imponemos el término fuente Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \mathbf{F}}
en la ecuación vectorial de CDR transitoria (7) mediante las siguientes expresiones tomadas de las ecuaciones (1), (2) y (3):
|
siendo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \mathbf{F}=[f_{1},f_{2},f_{3},f_{4}]^{T}}
y Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \bar{\tau }_{ji}}
y Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle Q_{i}}
dados por las ecuaciones (4) y (5), respectivamente. Hemos tomado batimetría constante con profundidad de 1 m, es decir, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle H=1}
m, aceleración de la gravedad Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle g=10}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \mathrm{m/s^{2}}}
, viscosidad cinemática Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \nu _{H}=10^{-3}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \mathrm{m^{2}/s}}
y los coeficientes empíricos de dispersión Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle k_{11}=k_{22}=10^{-3}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \mathrm{m^{2}/s},}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle k_{12}=k_{21}=0.}
El parámetro de Coriolis Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \hat{f},}
las tensiones de superficie libre debidas al viento Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \tau _{3i}^{s},}
las variaciones de presión atmosférica Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle p_{a}}
y el coeficiente de fricción en el fondo Ch no han sido tomados en cuenta para los ejemplos de las pruebas de convergencia en malla, como tampoco el término reactivo de la ecuación de transporte de contaminantes.
A continuación detallamos los resultados de los experimentos numéricos de las pruebas de convergencia en malla con solución analítica conocida, tanto para el método ASGS como para el OSS. En cada gráfica se puede apreciar con línea continua la pendiente teórica de convergencia y con línea con apéndices sobre ella la pendiente calculada. Presentamos los resultados para los distintos grados polinómicos de las funciones de forma estudiados, es decir, elementos lineales, cuadráticos, cúbicos y de cuarto orden triangulares Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle P_{1},\;P_{2},\;P_{3},\;P_{4}}
y elementos cuadrangulares Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle Q_{1},\;Q_{2},\;Q_{3},\;Q_{4}}
, respectivamente.
El dominio computacional es el cuadrado Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \left[0,1\right]\times \left[0,1\right]}
y el intervalo de tiempo es Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \left[0,1\right]}
, con incrementos para cada paso de tiempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \delta t=0.2} . La malla de elementos finitos consiste en triángulos o cuadrados formando una malla regular. Para cada grado polinómico de las funciones de forma Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle P_{1},\;P_{2},\;P_{3},\;P_{4}}
o Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle Q_{1},\;Q_{2},\;Q_{3},\;Q_{4},}
hemos calculado los errores con norma Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle L^{2}}
para ocho mallas de tamaño Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle h}
, siendo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle \frac{1}{h}=15,\;20,\;25,\;30,\;35,\;40,\;45,\;50,}
el número de partes en que se ha dividido cada lado del cuadrado. En la Tabla 1 se muestran el número de elementos y el número de nodos para cada refinamiento, tanto para elementos triangulares como para elementos cuadrangulares. Los valores de las constantes algorítmcas Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle c_{i}}
, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle i=1,2,3,4,}
se han calibrado a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle c_{1}=12,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle c_{2}=2,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://mathoid.scipedia.com/localhost/v1/":): {\textstyle c_{3}=1,}
y el integrador temporal utilizado es BDF3 (diferencias finitas hacia atrás de cuatro niveles de tiempo y tercer orden en ).
| Triángulos | Número de nodos | ||||
|---|---|---|---|---|---|
| elem. | |||||
| 15 | 450 | 256 | 961 | 2116 | 3721 |
| 20 | 800 | 441 | 1681 | 3721 | 6561 |
| 25 | 1250 | 676 | 2601 | 5776 | 10201 |
| 30 | 1800 | 961 | 3721 | 8281 | 14641 |
| 35 | 2450 | 1296 | 5041 | 11236 | 19881 |
| 40 | 3200 | 1681 | 6561 | 14641 | 25921 |
| 45 | 4050 | 2116 | 8281 | 18496 | 32761 |
| 50 | 5000 | 2601 | 10201 | 22801 | 40401 |
| Cuadrados | Número de nodos | ||||
|---|---|---|---|---|---|
| elem. | |||||
| 15 | 225 | 256 | 961 | 2116 | 3721 |
| 20 | 400 | 441 | 1681 | 3721 | 6561 |
| 25 | 625 | 676 | 2601 | 5776 | 10201 |
| 30 | 900 | 961 | 3721 | 8281 | 14641 |
| 35 | 1250 | 1296 | 5041 | 11236 | 19881 |
| 40 | 1600 | 1681 | 6561 | 14641 | 25921 |
| 45 | 2025 | 2116 | 8281 | 18496 | 32761 |
| 50 | 2500 | 2601 | 10201 | 22801 | 40401 |
En el encabezado de las gráficas de las pruebas de convergencia en malla de las Figuras 1 y 2 se adjuntan dos filas con los valores de las pendientes calculadas; la primera fila corresponde a los valores de las pendientes de las rectas que pasan por los primeros 5 puntos y la segunda fila son las pendientes de las rectas que pasan por los últimos 5 puntos de los 8 puntos del refinamiento de malla evaluados . De esta manera podemos visualizar numéricamente la tendencia de la convergencia de las pendientes calculadas hacia el valor teórico. Para el cálculo de dichas pendientes se ha utilizado el método de los mínimos cuadrados; la simbología corresponde a las pendientes para elementos triangulares: lineales, cuadráticos, cúbicos y de cuarto orden respectivamente, mientras que para elementos cuadrangulares lineales, cuadráticos, cúbicos y de cuarto orden la simbología es . Los valores de las pendientes teóricas para las variables de la velocidad y de concentración de un contaminante son , , , , y las pendientes teóricas para la variable , que es la elevación de la superficie libre del agua, son , , , .
En la Figura 1, se muestra la convergencia en malla para la primera componente de la velocidad usando elementos triangulares y en la Figura 2 la convergencia en malla para la concentración de un contaminante. Las otras variables muestran igualmente convergencia óptima para todos los elementos considerados. Lo mismo sucede con los elementos cuadrangulares.
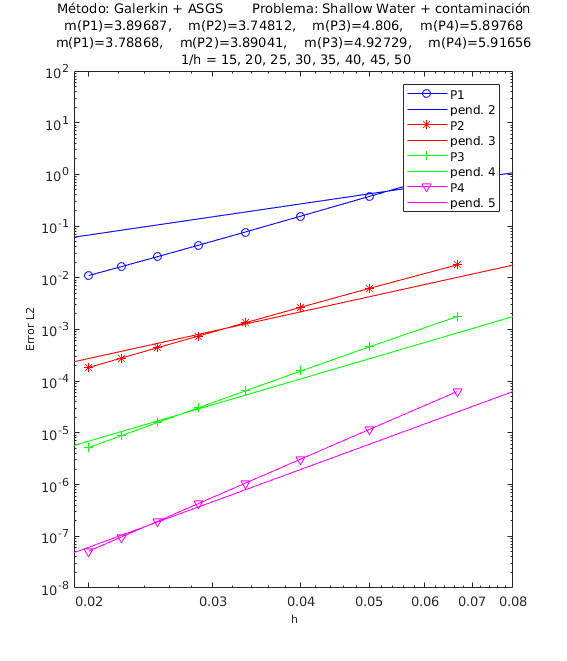
|
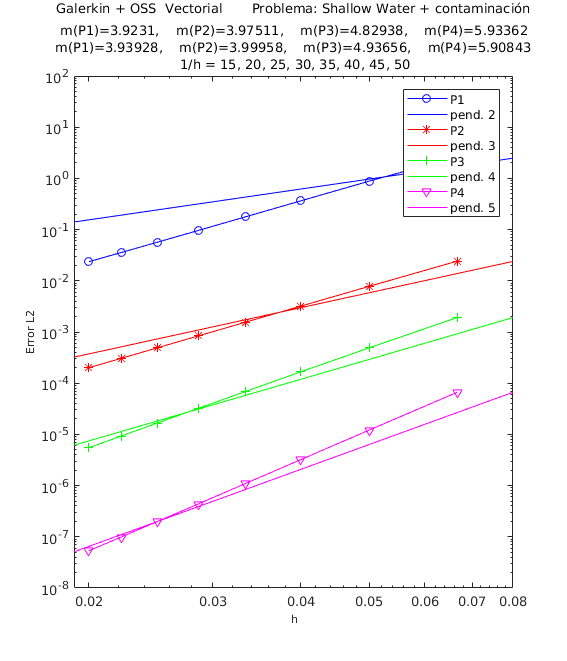
|
| Figura 1. Convergencia en malla ASGS-OSS, elementos triangulares, velocidad | |
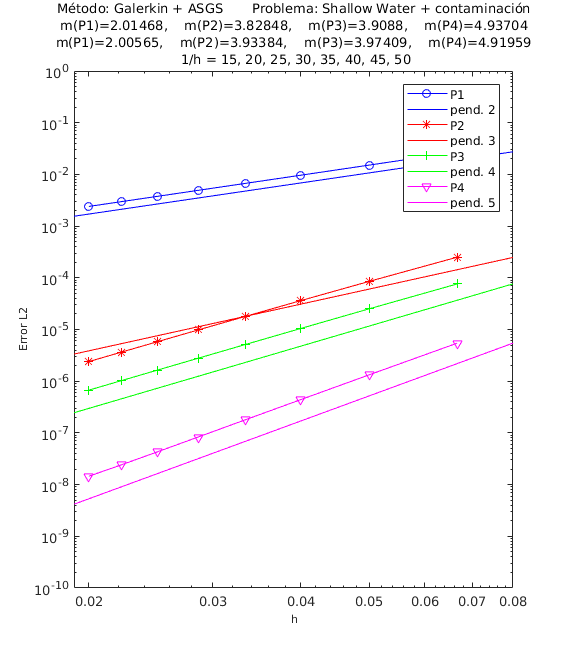
|
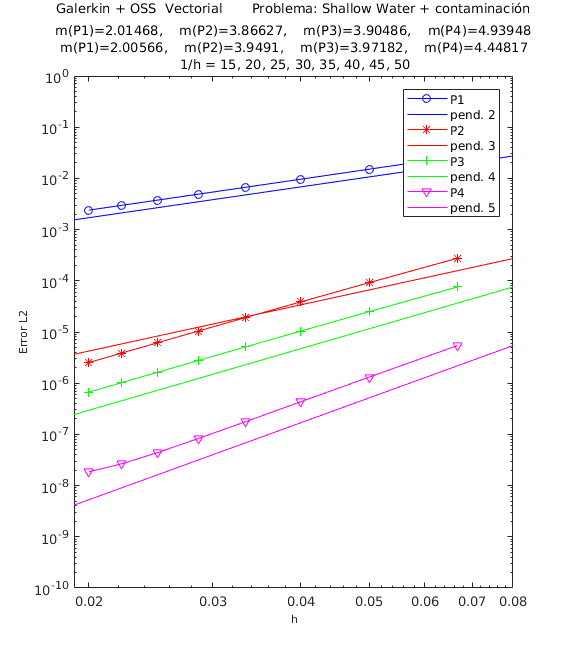
|
| Figura 2. Convergencia en malla ASGS-OSS, elementos triangulares, concentración | |
4.2 Transporte de un contaminante en una cavidad cuadrada
Este caso de referencia ha sido ampliamente examinado en la literatura con diferentes métodos, en [6] con el método de diferencias finitas, con el método de volúmenes finitos en [3,5], con el método SUPG en [4]; en todos los casos se ha considerado convección pura, es decir, el coeficiente empírico de dispersión del transporte de un contaminante se ha tomado nulo. En el presente trabajo vamos a reexaminar el caso de referencia con el método variacional ASGS y utilizando funciones de forma cuadráticas, cúbicas y de cuarto orden, en convección dominante, es decir, considerando el coeficiente empírico de dispersión y .
El dominio computacional es un canal cuadrado de 9 km km. En cuanto al mallado, con el objeto de comparar los resultados entre elementos lineales y de alto orden, hemos considerado conveniente utilizar refinamientos de malla para elementos y que den el mismo número de nodos entre si. Tomamos como referencia el refinamiento de malla para , que consta de elementos cuadrados uniformes de 9 nodos, es decir, el espaciado en las direcciones e es , con un total de 8100 elementos y 32761 nodos. De esta manera, la malla de referencia para elementos consta de 180180 elementos cuadrados uniformes de 4 nodos, es decir , con un total de 32400 elementos y 32761 nodos. La malla de referencia para elementos consta de elementos cuadrados uniformes de 16 nodos, es decir , con un total de 3600 elementos y 32761 nodos. Finalmente, la malla de referencia para elementos consta de 4545 elementos cuadrados uniformes de 25 nodos, es decir , con un total de 2025 elementos y 32761 nodos.
El tamaño del paso de tiempo es uniforme, con , y el integrador temporal es BDF3 en todos los casos.
Un flujo uniforme con y está impuesto en todo el dominio. La concentración inicial de contaminante está dada por la siguiente suposición de dos distribuciones Gausianas centradas respectivamente en y en , dada por:
|
|
donde , y .
Dada la baja difusión del problema, la solución exacta es aquella concentración de contaminante que se mueve diagonalmente a través del dominio con velocidad constante, preservándose su forma durante todo el tiempo. La Figura 3 ilustra los resultados usando el elemento comparados con la solución teórica en diferentes tiempos, observándose en todos los casos resultados completamente satisfactorios comparados con la solución exacta.
En la Tabla 2, presentamos los valores máximos y mínimos de concentración de contaminante para las funciones de forma , , y , en donde observamos que a partir de el error de aproximación al valor exacto máximo es del orden de las centésimas, por lo cual en la Figura 3 hemos usado los resultados del elemento .
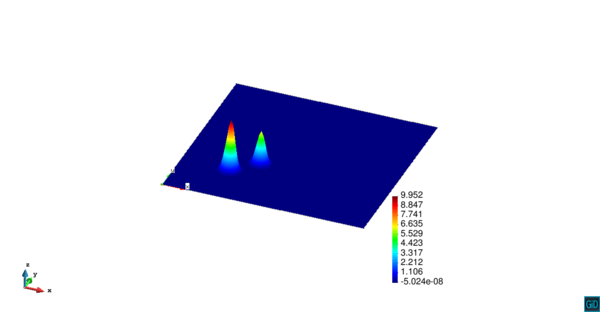
|
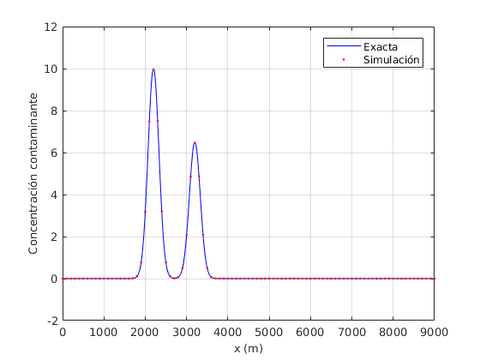
|
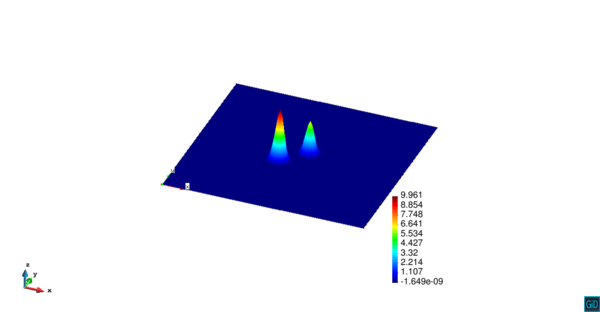
|
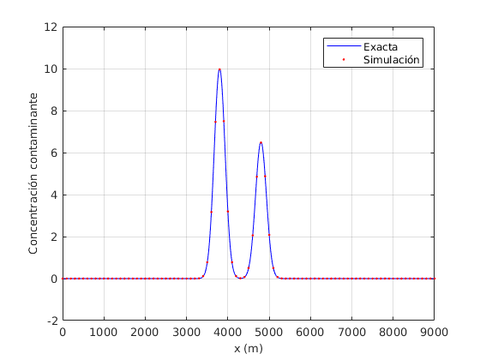
|
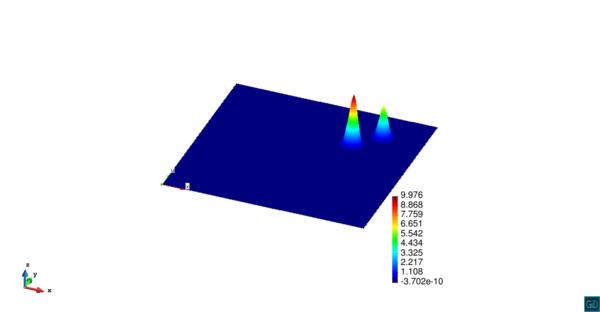
|
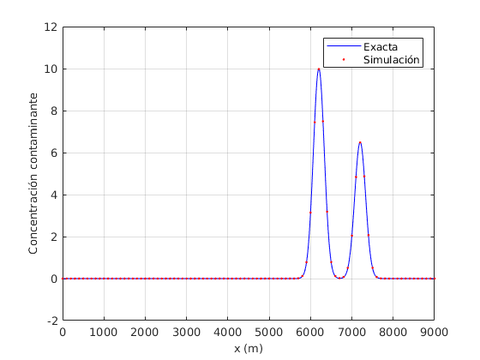
|
| Figura 3. Contornos 3D (izquierda) y distribución del contaminante (derecha) a lo largo de la diagonal de la cavidad cuadrada, con elementos | |
| Solución exacta | |||||
|---|---|---|---|---|---|
| Número de elementos | - | 32400 | 8100 | 3600 | 2025 |
| Número de nodos | - | 32761 | 32761 | 32761 | 32761 |
| Máximo valor de | 10 | 9.312 | 9.976 | 10.03 | 10.04 |
| Mínimo valor de | 0 |
4.3 Transporte de un contaminante en el golfo de Roses y en la desembocadura del río Guadalquivir
A continuación presentamos dos ejemplos numéricos del transporte de un contaminante. Ambos ejemplos corresponden a situaciones físicas reales, con geometrías complejas. El objetivo es mostrar que el modelo numérico propuesto puede ser utilizado en este tipo de situaciones, aunque no disponemos de valores experimentales con los cuales comparar los resultados y por consiguiente los mostraremos solamente de manera cualitativa, sin entrar en su discusión. Desde el punto de vista numérico, el valor de estos resultados es comprobar que no presentan ningún tipo de oscilación numérica, pese a utilizar igual interpolación para todas las variables y tratarse de situaciones de flujo con convección dominante.
Consideramos una concentración constante de un solo contaminante en el flujo de entrada y coeficientes de difusión constantes y . La suposición de que los coeficientes de difusión son constantes es debido a que los efectos de turbulencia no han sido considerados en el modelo. También asumimos que la concentración del contaminante se anula en las fronteras sólidas, por lo que prescribimos a cero dicha concentración tanto en el perfil de las costas como en las riveras del río, en los dos problemas tratados. En el resto de los contornos consideramos la concentración de contaminante libre, con concentración inicial igual a cero. En ambos ejemplos numéricos hemos considerado batimetría constante con una profundidad de m (no hemos considerado pues la disminución de la profundidad hasta ), la aceleración de la gravedad m/s y la viscosidad cinemática m/s. El parámetro de Coriolis , las tensiones de superficie libre debidas al viento , las variaciones de presión atmosférica y el coeficiente de fricción en el fondo no han sido tomados en cuenta en ninguno de los dos ejemplos.
El primer ejemplo es la simulación del transporte de un contaminante de concentración constante , debido a una corriente marina que viene desde el norte en el golfo de Roses sobre la costa catalana, al sur del Cabo de Creus. La geometría del problema y los resultados numéricos se muestran en las Figuras 4, 5 y 6. El dominio de simulación tiene dimensiones de aproximadamente 80 40 km. La malla de elementos finitos consiste en 6062 elementos triangulares lineales con 3217 nodos.
Una corriente marina de 0.1 m/s que llega desde el norte ha sido prescrita en el borde superior del dominio. Esto corresponde a una velocidad como flujo de entrada en la parte superior del dominio. En la costa la velocidad se prescribe a cero, mientras que en los contornos inferior y derecho del dominio se deja libre, donde la sobreelevación del agua se prescribe a cero.
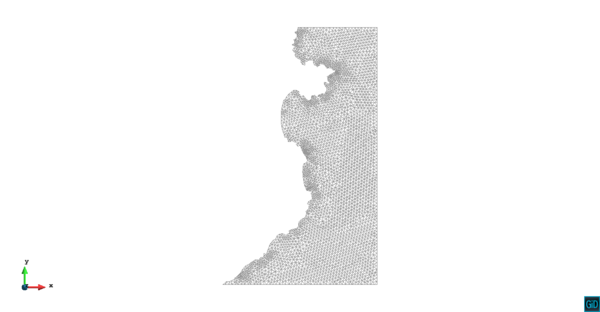
|
| Figura 4. Golfo de Roses. Geometría y malla de elementos finitos |
| |||||||||||||||
| Figura 6. Flujo alrededor del golfo de Roses. (a) Vectores de velocidad. (b) Concentración del transporte de un contaminante (INGOG 4) | |||||||||||||||
En la segunda simulación numérica consideramos el transporte de un contaminante de concentración constante en la desembocadura del río Guadalquivir, en la costa del sur de España. La geometría del problema y los resultados numéricos se muestran en las Figuras 7, 8 y 9.
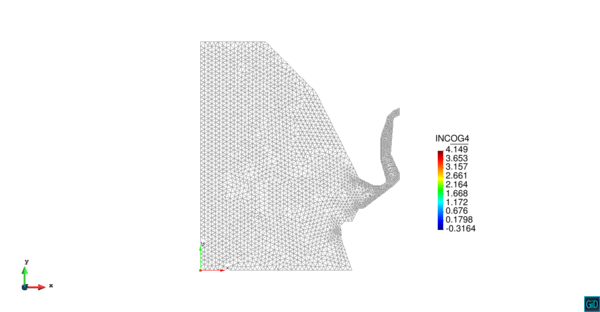
|
| Figura 7. Desembocadura del río Guadalquivir. Geometría y malla de elementos finitos |
| |||||||||||||||
| Figura 8. Flujo en la desembocadura del Guadalquivir. (a) Velocidad (máx: 0.83 m/s). (b) Elevación (INCOG3), superficie libre del agua (máx: 1.97 cm, mín: -1.42 cm) | |||||||||||||||
| |||||||||||||||
| Figura 9. Flujo en la desembocadura del Guadalquivir. (a) Vector de velocidad. (b) Concentración del transporte de un contaminante (INGOG 4) |
La malla de elementos finitos consiste en 4955 elementos triangulares lineales con 2645 nodos.
Un flujo de corriente marina de m/s está prescrito en el contorno inferior en dirección este-oeste y en la desembocadura del río se prescribe una corriente del río de 0.3 m/s, igualmente en dirección este-oeste. En el resto de la costa y en las riveras del río la velocidad se prescribe a cero, y se deja libre en los contornos izquierdo y superior, donde la sobreelevación del agua está prescrita a cero.
Los dos ejemplos numéricos considerados presentan flujos complejos, con importantes variaciones temporales y espaciales. Esto hace que los parámetros de estabilización sean muy variables elemento a elemento. Este hecho dificulta la convergencia de los esquemas iterativos. Puesto que y (en el caso de contaminantes) son escalas de tiempo, a menudo se toman proporcionales a , y esto se puede justificar con argumentos diversos [24]. En los problemas en los que la convergencia del esquema iterativo es costosa, hemos tomado una cota máxima para y proporcional a , de manera que los hemos redefinido en cada elemento como
|
|
(21) |
donde y son parámetros que hay que ajustar dependiendo del tamaño de la malla y del grado del polinomio de las funciones de forma. El valor de se sigue calculando mediante la expresión dada en (18).
Mediante experimentación numérica hemos calibrado los parámetros y . Para el primer ejemplo hemos considerado y con un paso de tiempo uniforme 100 s y para el segundo ejemplo y con 2500 s. En ambos casos hemos usado el integrador temporal BDF2 y presentamos resultados numéricos en diferentes instantes de tiempos de simulación, y s.
4.4 Modelo depredador-presa
Vamos a considerar como problema a resolver el modelo depredador-presa mostrado en [33], que es un sistema acoplado de ecuaciones transitorias de convección-difusión-reacción no lineales en el término de reacción y que describen espacial y temporalmente la dinámica poblacional de una presa y un depredador en términos de funciones de densidad continuas. Usaremos este problema como ejemplo de sistema con términos reactivos no lineales, con dos concentraciones que compiten entre ellas (en este caso no necesariamente contaminantes). Nos centraremos en el problema propiamente del modelo depredador-presa, suponiendo que la velocidad es conocida. Si embargo, la extensión al caso en el que la velocidad resulta de resolver las ecuaciones del modelo de aguas someras es inmediata. En este problema además es frecuente considerar la posibilidad de que la velocidad de transporte del depredador sea distinta a la de la presa, por lo que cuando introduzcamos estas velocidades de transporte mantendremos esta posible generalización.
4.4.1 Formulación del modelo depredador-pressa
La forma general del modelo es como sigue:
|
|
donde y representan las densidades de población de la presa y del depredador, respectivamente. y son los coeficientes de difusión. es la función de crecimiento de la población de la presa. La función representa el acto de depredación resultante en una disminución de la población de la presa y en un incremento en la población del depredador. es la eficiencia de la depredación, la cual determina el incremento de la población del depredador, siendo . Finalmente, es la función que determina la cantidad de mortalidad del depredador.
Una de las posibilidades para modelar las funciones , y es:
|
|
donde la función está modelada por el llamado modelo de Hollinger tipo II, en el cual representa la tasa de depredación y es la densidad media de saturación de la presa. Para modelar el crecimiento de la población de la presa usamos el llamado modelo logístico, donde representa la tasa de crecimiento de la población de la presa y es la capacidad de carga del sistema, y denota la cantidad máxima de población de la presa que es soportada por el dominio; en este trabajo asumimos el valor de la unidad para este parámetro. La función de mortalidad del depredador está dada por un término lineal, siendo su coeficiente.
El modelo anterior considera que no hay transporte convectivo ni del depredador ni de la presa. Este transporte puede deberse a que depredador y presa se encuentren en un medio fluido en movimiento, que se correspondería con el modelo general que hemos tratado anteriormente, pero también puede ser necesario introducir la convección a través de un patrón de migración estacional o migración hacia regiones de disponibilidad de recursos. El término de advección resultante modela el movimiento masivo de poblaciones. Con esto se obtiene el sistema depredador-presa que finalmente consideraremos, dado por el sistema de ecuaciones:
|
|
al cual hay que añadir las condiciones de contorno y condiciones iniciales. En estas ecuaciones, , El campo de velocidad para la presa es y para el depredador .
Escribiendo el sistema depredador-presa en el formato de la ecuación vectorial de CDR transitoria (7) tenemos:
|
|
(22) |
La matriz de los parámetros de estabilización utilizada para este problema, que está descrita en [33], es , con:
|
|
donde recordemos que corresponde al diámetro del elemento y es el orden polinomial de interpolación. Las variables y las tomamos calculadas en la iteración anterior del paso de tiempo actual.
4.4.2 Pruebas numéricas y resultados
Consideremos la ecuación (22) del modelo depredador-presa dentro de un cuadrado unitario , con condiciones de contorno de Dirichlet homogéneas y condiciones iniciales de las densidades de población de la presa y del depredador dadas por las distribuciones normales (23) y (24), respectivamente, escritas a continuación y mostradas en la Figura 10:
|
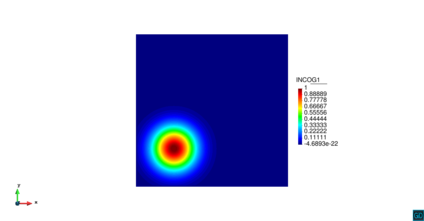
|
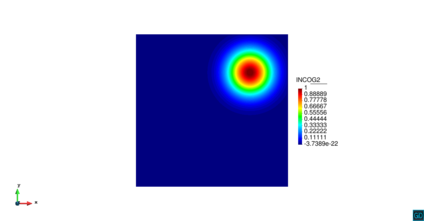
|
| Figura 10. Condición inicial de la densidad de población de la presa (izquierda) y del depredador (derecha) | |
En la Tabla 3 se encuentran los valores de los coeficientes de reacción y para varios casos de prueba que hemos considerado. Para todos estos casos de prueba los coeficientes de difusión se tomaron como m/s. El campo de velocidades se mantiene constante tanto para el depredador como para la presa. Las componentes de velocidad de la presa son m/s, m/s y para el depredador son m/s, m/s, con lo cual las poblaciones del depredador y de la presa son conducidas en direcciones opuestas para encontrarse frente a frente una con la otra. No consideramos ningún término fuente y las constantes y se tomaron a la unidad. Con esto el sistema de ecuaciones del modelo depredador-presa se escribe:
|
|
(25) |
| Caso 1 | 0 | 0 | 0 | 0 |
| Caso 2 | 0 | 0 | 0 | 1 |
| Caso 3 | 0 | 0 | 3 | 0.1 |
| Caso 4 | 1 | 0 | 3 | 0.1 |
| Caso 5 | 1 | 2 | 3 | 0.1 |
La malla de elementos finitos usada es regular y consta de elementos cuadrados de 4 nodos, es decir , con un total de 2500 elementos y 2601 nodos. El intervalo de tiempo es y el tamaño del paso de tiempo tomado es uniforme, con . Hemos usado el integrador temporal BDF2 y el método variacional multiescala ASGS descrito anteriormente. Presentamos resultados numéricos en diferentes instantes de tiempos de simulación, , , , para todos los casos de prueba.
En las Figuras 11, 12, 13, 14 y 15 se encuentran los resultados de los casos 1, 2, 3, 4 y 5, respectivamente, considerados en la Tabla 3. Los resultados numéricos en todos los casos son los esperados y corresponden con la realidad física de cada caso, observando además que son coincidentes con los resultados mostrados en [33].
Las diferencias de los resultados de las densidades de población del depredador y de la presa con elementos de alto orden (con 10201 nodos), (con 22801 nodos) y (con 40401 nodos) están en el orden de las milésimas con respecto a los resultados con elementos lineales para , tal como observamos en las Tablas 4 y 5, por lo que dependiendo de la escala del problema es suficiente la precisión con elementos lineales.
| |||||||||||||||
| Figura 11. Caso 1. Densidad de población de la presa (izquierda). Densidad de población del depredador (derecha) | |||||||||||||||
| |||||||||||||||
| Figura 12. Caso 2. Densidad de población de la presa (izquierda). Densidad de población del depredador (derecha) | |||||||||||||||
| |||||||||||||||
| Figura 13. Caso 3. Densidad de población de la presa (izquierda). Densidad de población del depredador (derecha) | |||||||||||||||
| |||||||||||||||
| Figura 14. Caso 4. Densidad de población de la presa (izquierda). Densidad de población del depredador (derecha) | |||||||||||||||
| |||||||||||||||
| Figura 15. Caso 5. Densidad de población de la presa (izquierda). Densidad de población del depredador (derecha) | |||||||||||||||
| Caso 1 | Caso 2 | Caso 3 | Caso 4 | Caso 5 | |
|---|---|---|---|---|---|
| 0.48614 | 0.48614 | 0.48614 | 0.69991 | 0.56545 | |
| 0.48847 | 0.48847 | 0.48847 | 0.70560 | 0.56853 | |
| 0.48847 | 0.48847 | 0.48847 | 0.70709 | 0.56928 | |
| 0.48848 | 0.48848 | 0.48848 | 0.70786 | 0.56982 |
| Caso 1 | Caso 2 | Caso 3 | Caso 4 | Caso 5 | |
|---|---|---|---|---|---|
| 0.48614 | 0.22615 | 0.63921 | 0.70337 | 0.65541 | |
| 0.48847 | 0.22685 | 0.63872 | 0.71223 | 0.66228 | |
| 0.48847 | 0.22684 | 0.63954 | 0.71348 | 0.66352 | |
| 0.48848 | 0.22684 | 0.64002 | 0.71412 | 0.66422 |
5. Conclusiones
En este artículo se ha presentado la aproximación del modelo acoplado de las ecuaciones del movimiento de un fluido en aguas poco profundas junto con las ecuaciones de convección-difusión-reacción del transporte de contaminantes mediante formulaciones estabilizadas de elementos finitos de alto orden (hasta el cuarto orden).
Las formulaciones estabilizadas de elementos finitos para la ecuación vectorial de CDR transitoria, ASGS y OSS, nos permiten utilizar igual interpolación en todas las variables, que para el modelo del transporte de contaminantes en aguas poco profundas son las dos componentes de velocidad , , la elevación de la superficie libre del agua y las concentraciones de contaminantes. Asimismo, las formulaciones ASGS y OSS para la ecuación vectorial de CDR transitoria nos permiten tratar con flujos de convección y reacción dominantes, incluyendo problemas no lineales en los términos convectivos y reactivos. Como ejemplo de problema de reacción no lineal hemos presentado el modelo depredador-presa, con dos concentraciones acopladas a través del término reactivo como incógnitas.
Para utilizar elementos finitos de alto orden, en la matriz de los parámetros de estabilización se ha incluido la dependencia con el orden polinomial de interpolación.
Los resultados de las gráficas de convergencia muestran claramente que las formulaciones para los métodos estabilizados ASGS y OSS son capaces de aproximar correctamente el problema vectorial transitorio de CDR con convección dominante, particularizado al sistema acoplado de cuatro ecuaciones correspondientes al flujo en aguas poco profundas y transporte de un contaminante.
Los resultados calculados del transporte de un contaminante en una cavidad cuadrada no muestran errores significativos de dispersión o disipación, por lo que concuerdan muy bien con los valores teóricos, y son mejores que los resultados presentados en la literatura, como en [3,4,5].
Asimismo, se observa que los resultados obtenidos del transporte de un contaminante en el golfo de Roses y en la desembocadura del río Guadalquivir son completamente satisfactorios, tanto para el campo de velocidades y el nivel de la superficie libre del agua como para la distribución de la concentración de un contaminante.
Finalmente los resultados del modelo depredador-presa son coherentes con la realidad física de cada caso, y muestran la robustez de las formulaciones estabilizadas ASGS y OSS para la ecuación vectorial de CDR transitoria en problemas de reacción dominante y de no linealidad en el término de reacción.
Agradecimientos
R. Codina agradece la ayuda recibida a través del programa ICREA Academia, del Gobierno de Catalunya.
Referencias
[1] Zlatev Z. The air pollution problem. In: Computer Treatment of Large Air Pollution Models, Environmental Science and Technology Library, vol 2, Springer, Dordrecht, 1995.
[2] Zienkiewicz O.C., Taylor R.L. The Finite element method. Fluid Mechanics. Butterworth- Heinemann, vol. 3, 5th edition, 2000.
[3] Li S., Duffy C.J. Fully-coupled modeling of shallow water flow and pollutant transport on unstructured grids. Procedia Environmental Sciences, 13:20982121, 2012.
[4] Behzadi F., Newman III J.C. A Semi-discrete SUPG method for contaminant transport in shallow water models. Procedia Computer Science, 80:1313-1323, 2016.
[5] Benkhaldoun F., Elmahi I., Seaïd M. Well-balanced finite volume schemes for pollutant transport by shallow water equations on unstructured meshes. J. Comput. Phys., 1:180-203, 2007.
[6] Komatsu T., Ohgushi A.K., Asai K. Refined numerical scheme for advective transport in diffusion simulation. J. Hydraul. Eng., 123:41-50, 1997.
[7] Begnudelli L., Sanders B.F. Unstructured grid finite-volume algorithm for shallow-water flow and scalar transport with wetting and drying. Journal of Hydraulic Engineering, 132(4):371-384, 2006.
[8] Cea L., Vázquez-Cedón M.E. Unstructured finite volume discretisation of bed friction and convective flux in solute transport models linked to the sallow water equations. Journal of Computational Physics, 231(8):3317-3330, 2012.
[9] Caleffi V., Valiani A. A 2D local discontinuous Galerkin method for contaminant transport in channel bends. Computers & Fluids, 88:629-642, 2013.
[10] Pavan S., Hervouet J.M., Ricchiuto M., Ata R. A second order residual based predictorcorrector approach for time dependent pollutant transport. Journal of Computational Physics, 318:122141, 2016.
[11] Cai L., Xie W.-X., Feng J.-H., Zhou J. Computations of transport of pollutant in shallow water. Applied Mathematical Modelling, 31:490498, 2007.
[12] Postma L., Hervouet J.-M. Compatibility between finite volumes and finite elements using solutions of shallow water equations for substance transport. Int. J. Numer. Methods Fluids, 53(9):14951507, 2007.
[13] Pavan S., Ata R., Hervouet J.-M. Finite volume schemes and residual distribution schemes for pollutant transport on unstructured grids. Environ. Earth Sci., 74:73377356, 2015.
[14] Liu H., Zhou J.G., Li M., Zhao Y. Multi-block lattice Boltzmann simulations of solute transport in shallow water flows. Advances in Water Resources, 58:24-40, 2013.
[15] Hammou H., Ginzburg I., Boulerhcha M. Two-relaxation-times lattice Boltzmann schemes for solute transport in unsaturated water flow with a focus on stability. Adv Wat Res., 4(6):779-793, 2011.
[16] Zhou J.G. A lattice Boltzmann method for solute transport. Int J Numer Methods Fluids, 61:848-63, 2009.
[17] Codina R., Badia S., Baiges J., Principe J. Variational multiscale methods in computational fluid dynamics. In: Encyclopedia of Computational Mechanics, E. Stein, R. Borst and T.J.R. Hughes (eds.), doi: 10.1002/9781119176817.ecm21172017, 2017.
[18] Rogers B., Fujihara M., Borthwick A.G.L. Adaptive Q-tree Godunov-type scheme for shallow water equations. Int J Numer Methods Fluids, 35:247-80, 2001.
[19] H. Yamamoto. Lecture 8: The shallow-water equations. June 2009, 9pp. https://www.coursehero.com/file/35480149/othersonline-HW4pdf/
[20] Hughes T.J.R. Multiscale phenomena: Green's functions, the Drichlet-to-Neumann formulation, subgrid scale models, bubbles and the origins of stabilized methods. Computer Methods in Applied Mechanics and Engineering, 127(1-4):387-401, 1995.
[21] Hughes T.J.R., Feijóo G.O., Mazzei L., Quincy J.B.. The variational multiscale method-a paradign for computational mechanics. Computer Methods in Applied Mechanics and Egineering, 166:3-24, 1998.
[22] Codina R. On stabilized finite element methods for linear systems of convection-diffusion-reaction equations. Computer Methods in Applied Mechanics and Engineering, 188:61-82, 2000.
[23] Codina R. A stabilized finite element method for generalized stationary incompressible flows. Computer Methods in Applied Mechanics and Enginineering, 190:2681-2706, 2001.
[24] Codina R. Comparison of some finite element methods for solving the diffusion-convection-reaction equation. Computer Methods in Applied Mechanics and Engineering, 156:185-210, 1998.
[25] Codina R., Blasco J. Analysis of a stabilized finite element approximation of the transient convection-diffusion-reaction equation using orthogonal subscales. Computing and Visualization in Science, 4:167-174, 2002.
[26] Codina R. Stabilized finite element approximation of transient incompressible flows using orthogonal subscales. Computer Methods in Applied Mechanics and Engineering, 191:4295-4321, 2002.
[27] Villota A., Codina R. Approximation of the shallow water equations with higher order finite elements and variational multiscale methods. Rev. int. métodos numér. cálc. diseño ing., 34(1), 28, 2018. URL https://www.scipedia.com/public/Villota_Codina_a.
[28] Codina R. Finite element approximation of the convection-diffusion equation: subgrid-scale spaces, local instabilities and anisotropic space-time discretizations. In Bail 2010 - Boundary and Interior Layers, Computational and Asymptotic Methods, Lecture Notes in Computational Science and Engineering, C. Clavero, J.L. Gracia and F.J. Lisbona (eds.), vol. 81, pages 85-97, Springer, 2011.
[29] Codina R., González-Ondina J.M., Díaz-Hernández G., Principe J. Finite element approximation of the modified Boussinesq equations using a stabilized formulation, International Journal for Numerical Methods in Fluids, 57:1249-1268, 2008.
[30] Villota A., Codina R. Approximation of the scalar convection-diffusion-reaction equation with stabilized finite element formulations of high order. Rev. int. métodos numér. cálc. diseño ing., 35(1), 6, 2019. URL https://www.scipedia.com/public/Villota_Codina_a
[31] Principe J., Codina R. On the stabilization parameter in the subgrid scale approximation of scalar convection-diffusion-reaction equations on distorted meshes. Computer Methods in Applied Mechanics and Engineering, 199:1386-1402, 2010.
[32] Codina R. On hp convergence of stabilized finite element approximations of the convection-diffusion equation. SeMA Journal, 75:591-606, 2018.
[33] Sheshachala S.K., Codina R. Finite element modeling of nonlinear reaction-diffusion-advection systems of equations. International Journal of Numerical Methods for Heat & Fluid Flow, 28(11):2688-2715, 2018. https://doi.org/10.1108/HFF-02-2018-0077
Document information
Published on 12/01/21
Accepted on 22/10/20
Submitted on 04/03/20
Volume 37, Issue 1, 2021
DOI: 10.23967/j.rimni.2020.10.007
Licence: CC BY-NC-SA license