| Line 85: | Line 85: | ||
<li> Adjusting <math>w</math> to the equation:</li> | <li> Adjusting <math>w</math> to the equation:</li> | ||
| − | + | <center> | |
<math display="inline">w(i+1)=E\left[xg\left(w^T(i)x\right)\right]-E\left[xg{}'\left(w^T(i)x\right)\right]w(i)</math>; | <math display="inline">w(i+1)=E\left[xg\left(w^T(i)x\right)\right]-E\left[xg{}'\left(w^T(i)x\right)\right]w(i)</math>; | ||
| − | + | </center> | |
| − | + | ||
<li> Implementing normalization processing, and <math display="inline">w(i+1)=w_i/\Vert w_i\Vert </math>. If <math display="inline">\vert w(i+1)-w_i\vert <\epsilon </math>, the algorithm is determined to converge, which can arrive at an EIC. Or else, the algorithm cannot converge, which needs to go back to the steps (4) and (5) for further iteration;</li> | <li> Implementing normalization processing, and <math display="inline">w(i+1)=w_i/\Vert w_i\Vert </math>. If <math display="inline">\vert w(i+1)-w_i\vert <\epsilon </math>, the algorithm is determined to converge, which can arrive at an EIC. Or else, the algorithm cannot converge, which needs to go back to the steps (4) and (5) for further iteration;</li> | ||
| Line 106: | Line 105: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>S_k=\sum_{l=1}^mP_k\left(X_{kl},Y_{kl}\right)</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (4) | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) | ||
Revision as of 13:47, 30 September 2020
Abstract
The key to an acoustic signal lies in its frequency spectrum characteristics, and the primary premise of noise reduction is the identification of main noise sources. In this paper, an approach to noise source identification is introduced based on the improved fast independent component analysis (FastICA) algorithm for blind source signals to correct the uncertainty of traditional FastICA. Taking the measured noise signals radiated from a forklift at idle speed as an application case, two obvious estimated independent components (EICs) and their corresponding frequency spectrums were obtained. In addition, the result of numerical identification of sound sources is verified by scaning and paint system (SPS) and the error is less than 5%. Base on the spectral characteristics analysis, the improvement measurement of the target forklift was performed, and the results indicated that the sound power level of radiated noise from the whole vehicle is effectively reduced by 1.75dB, and meets the domestic industry requirement.
Keywords: Noise reduction, improved FastICA, frequency spectrum characteristics, forklift
1. Introduction
As we all know, fuel engineering vehicles are widespread, resulting in the radiated noise decibel level far greater than 90dB, which brings the interference of hearing and mental health to people's lives, especially the drivers who have been in this environment for a long time [1]. Therefore, the limit noise reduction of vehicles, to meet the requirements of the industry, has been a continuous work. However, due to the complexity of vehicle internal structure and the randomness of driving conditions, the noise emitted by the engine exhibits obvious blind source characteristics, which makes it difficult to identify the sound sources [2,3]. It is worth mentioning that independent component analysis (ICA) is the most common technique to achieve blind source separation (BSS) and has been successfully solve various practical problems, for instance, feature extraction [4], structural damage detection [5,6], biomedical signal separation [7], vibration-based diagnostics [8] and image classification [9]. Guadalupe Lopez P [3] pointed out that ICA and wavelet technology can be used to extract signal features and separate noise sources in the actual environment. Furthermore, in order to reduce and control environment noise, a method based on BSS was presented to achieve noise source separation [10]. Cheng et al.[11] studied an enhanced ICA for separating and locating noise sources of mechanical systems. Zhang et al. [12] once successful carried out de-noising experiments by the use of different algorithms, namely ICA algorithms and adaptive signal processing algorithms. The results indicated that FastICA algorithm is the most effective for reducing noise. In detail, FastICA is a fixed-point algorithm based on maximum negentropy with significant advantages of fast convergence and small calculation and initially put forward by Hyvarinen [13]. Whereas, many previous research findings have shown that the order, phase and amplitude directly related with noise energy may be changed by FastICA algorithm [14-15]. Therefore, the traditional FastICA needs to be improved for determining the main noise sources.
This paper is to propose a noise reduction method based on the spectrum characteristic analysis for main noise sources and carry out the application research on a forklift, in which correcting the energy information of source signals is an important prerequisite for the main noise source identification.
2. Improved FastICA algorithm
Assuming that the time difference between signal sources arriving at the sensor is not considered, there are n signal sources with unknown statistical independents and m sensors (), and the observation signals received by sensors are formed by linear mixing of the source signals, which is expressed as [3,11]
|
|
(1) |
where and denotes source signals and observation signals, respectively; represents a mixed matrix. The analysis method of ICA is to search for a separation matrix and make the equal to . Finally, the output approximate to source signals can be calculated and obtained under two basic conditions , which can be expressed as
|
|
(2) |
The two basic conditions need to be satisfied to utilize FastICA algorithm: 1) Source signals are statistically independent with each other; 2) At most one source signal follows the Gaussian distribution.
The FastICA algorithm is based on the maximization of non-Gaussian using the fixed iterative theory and takes negative entropy as the objective function expressed by the following approximate formula [16-17]
|
|
(3) |
where is the negentropy of , is a random variable with zero mean and unit variance, and , is a constant, is mean operation, is a non-quadratic function and is a standard Gaussian variable.
Based on the maximization of negative entropy, the detailed realization of the FastICA algorithm is as follows [18-19]:
- Applying mean processing to the data , then
- Applying whitening process to the data and orthogonal transformation to the EICs, and ;
- Establishing the convergence error to be ;
- Supposing ;
- Adjusting to the equation:
- Implementing normalization processing, and . If , the algorithm is determined to converge, which can arrive at an EIC. Or else, the algorithm cannot converge, which needs to go back to the steps (4) and (5) for further iteration;
- If the algorithm converges, all EICs can be figured out based on the separation matrix and Eq. (2). As to the uncertainty of EICs in order, phase and amplitude, this paper presents the method to correct the EICs by written MATLAB program based on fast fourier transform (FFT) and maximum spectrum similarity (MSS)[18]. The main idea is as below: Firstly, the spectral characteristics of the acquired observation signals and EICs are analyzed; secondly, the difference between the maximum and minimum spectral amplitudes of the current signals is divided into m groups for figuring out the spectrum similarity; furthermore, the maximum similarity value is regarded as the EIC from the corresponding channel. Finally, the uncertainty of EICs is corrected in terms of phase and amplitude. The specific implementation process is as below:
- Applying FFT to the th channel of observed signal and the th EIC obtained by traditional FastICA algorithm;
- Reprocessing the spectrum. A maximum point that contains main information in the spectrum is to be found, and points from both its left side and right side are reserved. To enhance the feature of main information, the rest points are all processed to be zero;
- Processing the spectrum by groups with different amplitude. Since the signals have been whitened, uncertainty emerges among the spectrum amplitudes. In order to unify the scaling standard, the difference between the minimum and maximum spectrum amplitudes of current signals is figured out, and the result is divided into groups, namely and are generated; After reprocessing and grouping the signals in the th channel, the corresponding frequency of the EICs in every spectrum and every group is to be checked. If there is non-zero spectrum amplitude, the frequency is considered to be 1; otherwise, the frequency is zero. Calculate the spectral similarity between and . The spectral similarity can be calculated by
where indicates the probability of two signals occurring at the same position. Based on this definition, a similarity coefficient can be obtained, and when has a maximum, the corresponding EIC is considered as the signal . Therefore, the observed signals of the channel can be matched with the identified EIC. Likewise, the signals of the other channels and all the remaining EICs also can be identified, and the above steps can be repeated to complete the order of all EICs;(4) - Adjusting the phase. The phase of the obtained EIC is often opposite to that of the original signal. Therefore, if the sum of observed signal and the ordered EIC is lower than their difference, the phase is considered to reverse. And then corresponding phase adjustment is needed for the EIC;
- Adjusting the amplitude. Among the EICs having been ordered, a component spectrum with relative high amplitude and unique frequency is to be chosen as a benchmark. And then, the EIC is multiplied by appropriate weight factor so that the EIC under this frequency and the observed signal have the same spectrum amplitude. Therefore, the EIC is considered to be the corresponding source signal with consistent amplitude.
;
3. Main noise sources and spectrum analysis
3.1 Noise signal measurement
In order to verify the feasibility the above improved FastICA algorithm for solving practical engineering problems, an internal combustion forklift is taken as the research case, and its engine cabin mainly has three parts of an engine system with four cylinders and four strokes, a cooling system and intake and exhaust systems.
Considering the large size of the vehicle, the noise signal measurement was processed in the professional outdoor venue with the use of ZonicBook/618E noise test system. According to the sound power measurement standard, 9 measurement points were arranged [11]. This noise test was conducted under the windless and quiet environment and the idle speed of 671 rpm [20]. After the prototype comes to a stable working condition, the acquisition test can be started. To be clear, the sampling frequency was set to 25.6KHZ and 9 groups of data were ultimately obtained.
3.2. Noise source identification
In practice, the noise excitation source of the forklift is numerous, mainly from the combustion system, piston system, cooling fan, intake and exhaust systems. From these different sources, different noises can be generated, but with a clear time-dependent excitation and frequency range in the time-frequency domain. This independent distribution in time and space satisfies the prerequisite that source signals must be independent to each other [20]. Owing to the linear transformation of signals, it can be seen that the collected observation signals and the noise source signals have equivalent non-Gaussian [11]. Thus, the following part is to calculate and analyze the non-Gaussian of the observed signals.
In general, the kurtosis value of the 4-order statistic is taken as the basis for quantitative judgment of non-Gaussian signals [21]. The kurtosis of a random variable z is defined as
|
|
(5) |
In the equation, is an average value; is a standard deviation; E is a mathematical expectation. When x is in a Gaussian distribution, ; When it is in super–Gaussian distribution, ; When it is in sub–Gaussian distribution, .
By Eq.(5), the kurtosis values of nine measured noise signals can be easily obtained. When comparing to the Gaussian signal (its kurtosis is 3), it shows that there are 6 kurtosis values greater than 3, and 3 kurtosis values less than 3. It can be found that the signals collected in this test have non–Gaussian, which satisfies the assumed condition of FastICA analysis. Therefore, the improved FastICA algorithm can be utilized to separate the noise sources of the forklift. After blind source separation, nine EICs were obtained, and the contribution of EICs could be solved below.
There are two sound sources whose sound pressures are assumed to be PA and PB, and their synthetic sound pressure is PC, which is calculated by
|
|
(6) |
Thus, the synthetic sound pressure level LPC is derived as
|
|
(7) |
Where P0 (P0=2×10-5 Pa) is the reference sound pressure. It is supposed that in a free space a point sound source sends out sound waves and the sound intensity of r meter(s) distance from the sound source is Ir. Consequently, its sound power is Wr= ( ) and the sound pressure level is LP (LP=20lg(P/P0)). Thus, the sound power LW is given by
|
|
(8) |
And then, the sound power W is calculated as: , where W0 is the reference sound power and W0 =10-12W.
Through the noise test system, the effective value of the sound pressure in each channel can be gained. When substituting these values to above relevant acoustic formulas, it is easy to get the sound power of noise signal from every measuring point as well as EICs and the total radiated sound power, as shown in Tables. 1 and 2. The noise contribution defined as the ratio of each EIC’s sound power to the total radiated sound power can be described as
|
|
(9) |
Where WTotal and Wi represent synthetic sound power of all measuring points and the sound power of the ith EIC.
The noise contribution of nine EICs from y1 to y9was calculated to be 4.61%, 42.82%, 3.85%, 2.12%, 6.4%, 33.18%, 2.35%, 1.27%, 3.4%, respectively. And it is obvious that among the EICs, y2 and y6 are the most prominent ones, that is, the primary and secondary noise sources of this case.
| Noise signal | P (Pa) | LP(dB) | LW(dB) | W(W) |
| x1 | 1.226 | 95.749 | 106.749 | 0.0473 |
| x2 | 2.171 | 100.713 | 111.713 | 0.1484 |
| x3 | 1.28 | 96.124 | 107.124 | 0.0516 |
| x4 | 0.765 | 91.653 | 102.653 | 0.0184 |
| x5 | 1.083 | 94.672 | 105.672 | 0.0369 |
| x6 | 1.057 | 94.461 | 105.461 | 0.0352 |
| x7 | 0.923 | 93.283 | 104.283 | 0.0268 |
| x8 | 0.982 | 93.822 | 104.822 | 0.0304 |
| x9 | 1.261 | 95.994 | 106.994 | 0.05 |
| Synthetic | 3.76 | 105.483 | 116.483 | 0.4449 |
| Noise signal | P (Pa) | LP(dB) | LW(dB) | W(W) |
| y1 | 0.807 | 92.12 | 103.12 | 0.0205 |
| y2 | 2.461 | 101.8 | 112.8 | 0.1905 |
| y3 | 0.738 | 91.34 | 102.34 | 0.01713 |
| y4 | 0.548 | 88.75 | 99.75 | 0.00943 |
| y5 | 0.952 | 93.55 | 104.55 | 0.0285 |
| y6 | 2.165 | 100.69 | 111.69 | 0.1476 |
| y7 | 0.577 | 89.2 | 100.2 | 0.01046 |
| y8 | 0.424 | 86.52 | 97.52 | 0.00565 |
| y9 | 0.693 | 90.79 | 101.79 | 0.0151 |
| Synthetic | 0.807 | 92.12 | 103.12 | 0.0205 |
The calculation result is shown in Figure 2, and it obvious that the main noise sources are independent components y2 and y6.
The next work is to identify the two main noise sources and spectrum analysis. First of all, it is necessary to point out that the noise signal from engine cabin of the forklift is a complex wideband signal. Therefore, it is difficult to recognize noise accurately only by FFT analysis, and the time-domain information of acoustic signal needs to be considered simultaneously [20].
The previous study indicated that the Morlet wavelet was widely used in time-domain analysis, which is defined as[22-24]:
|
|
(10) |
Where fb and fc are the bandwidth parameter and the center frequency, respectively. In this case, fb=2 and fc=1.5.
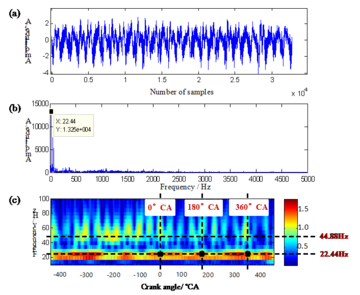
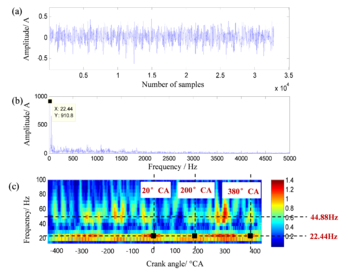
The radiated noise energy of the vehicle changes over time, which can be reflected by the change of the crank angle. Generally, the ignition time of an engine is set based on the crank angle. When the piston motion moves to the top dead center, the crank angle is 0 °CA. With the use of FFT and continuous Morlet wavelet transform (MWT), spectrum analyses were carried out on the two EICs [20]. The results are shown in Figure 1 and Figure 2.
Figure 1 presents that the major energy of independent component y2 concentrates in the lower frequency band; the peak spectrum appears in the frequency of 22.44Hz, and the twice frequency, 44.88Hz, takes the second place; the waveform of y2 and the change of crank angle indicate that y2 is periodic; the information of time domain also shows that the peak value of 22.44Hz appears at zero, 180 and 360 degrees of crank angle. In this test, the engine is 4-cylinder 4-stroke, and its operating condition is idle speed, i.e. 671 rpm. The formula for calculating the fundamental frequency of engine combustion can be expressed as f=vl/(60t) [25], here, v is the running speed of the engine; l and t represent the number of cylinders and stroke coefficient respectively, and t=2 for the four strokes. The ignition frequency of the engine at this moment can be calculated as 22.37 Hz by Eq.(11). The second harmonic frequency of the fundamental frequency is 44.88 Hz, and the ignition interval angle is 720 0°CA/4=180 0°CA. Therefore, it can be determined that the base frequency noise of the engine combustion corresponds to the independent component y2.
It can be found that, in Figure 2, the energy of y6 is peaked at 22.44Hz, and the variations of the waveform and crankshaft indicate that y6 is also periodic. The base frequency generated by the exhaust system of the diesel engine is 22.44 Hz, which is consistent with the fundamental frequency of the combustion noise [25]. In the test, the exhaust fundamental-frequency noise of the prototype is generated about 20 °CA after the top dead center, corresponding to Figure 2(c). Thus, the independent component y6 is the exhaust fundamental-frequency noise
4. Experimental verification based on scaning and paint system (SPS)
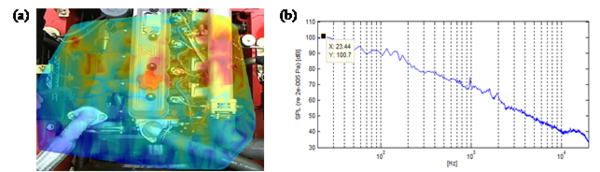
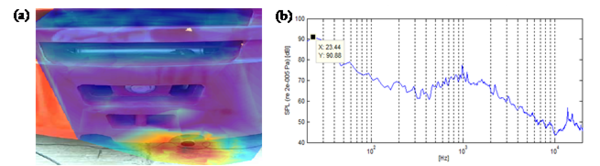
In order to verify the accuracy of numerical results, SPS is adopted for the noise source identification test on the same prototype. The basic measurement process of the system is as follows: while a PU probe is scanning, firstly, the camera tracks the moving trajectory of the probe and forms the graphic grids; and then the system software automatically synchronizes the audio and video signals and output the measured values directly; lastly, key acoustic parameters can be figured out including pressure and intensity of sound field, which are further presented with high-resolution nephogram.
The identification test is carried out in parallel with the noise acquisition test, namely, the test conditions are both idle speed of 671 rpm [20]. The positions of the acoustic scanning are at the top of the open engine cabin and the exhaust pipe. Through the scanning test, the main acoustic parameters mentioned above can be calculated. The results obtained by post processing are illustrated in Figure 3 and Figure 4.
Figure 3. Experimental identification results of the open engine compartment. (a)Sound color map; (b) Sound power spectrum.
Figure 4. Experimental identification results of the exhaust pipe. (a)Sound color map; (b) Sound power spectrum.
Figure 3 and Figure 4 indicate that noise energies radiated from the engine cabin and exhaust pipe mainly concentrate in the low-frequency band. The peak spectrum is generated by frequency component 23.44Hz, in which the relative error between 23.44Hz and the calculated value (22.44 Hz) is less than 5%. It proves that the proposed method for noise source separation based on the improved FastICA algorithm is of high accuracy and has important practical application.
5. Noise reduction test
Based on the aforementioned findings, spectrum of radiated noise from the forklift is mainly concentrated in low frequency. The de-noising test adopted sound-absorbing materials with high absorption coefficient in low frequency band, and the materials were covered the whole top of engine cabin exhibited in Figure 5 [26]. According to the test standard of JB/T3300-2010, the noise radiation results of at the modes of lifting, operating and idling are respectively achieved and described in Table 3 to Table 5.
| Test number | Measuring point 1 | Measuring point 2 | Measuring point 3 |
| 1 | 82.4 | 80.6 | 80.1 |
| 2 | 80.6 | 79.9 | 79.2 |
| 3 | 80.6 | 80.1 | 79 |
| 4 | 82.8 | 82.3 | 83.7 |
| Test number | Measuring point 1 | Measuring point 2 | Measuring point 3 |
| 1 | 79.6 | 79.5 | 79.3 |
| 2 | 78.7 | 77.8 | 77.2 |
| 3 | 79.1 | 77.9 | 78.1 |
| 4 | 80.6 | 79.4 | 78.8 |
| Test number | Measuring point 1 | Measuring point 2 | Measuring point 3 |
| 1 | 64.2 | 63.1 | 63.7 |
| 2 | 62.9 | 64.4 | 62 |
| 3 | 62 | 64.3 | 61.7 |
| 4 | 63.6 | 62.9 | 64.2 |
According to the noise limit standard of JB/T2391-2007, the total radiated sound power level of the prototype is calculated to be 104.13 dB(A). Compared to the decibel level of 105.88 dB(A) before the modification, the level has been reduced by 1.75 dB(A), which is basically satisfy the domestic noise radiation requirement in the forklift industry and recognized by the cooperative enterprise(XGMA).
6. Conclusion
Focused on the noise reduction, this paper takes the frequency spectral characteristics of the primary and secondary noise sources as the starting point. The separation and identification of main noise sources are important prerequisites for this study. In view of the uncertainties of the EICs, this paper presents the improved FastICA algorithm based on FFT and MSS and combines MWT technique to identify and calculate the primary and secondary noise sources of the forklift during the idle condition. With the use of SPS, the noise source scanning experiment is conducted on the same prototype and condition. The error between the experiment result and the calculated result by the algorithm is less than 5%, which verifies the accuracy and reliability of the improved FastICA algorithm. Furthermore, the spectral analysis of the main noise sources indicates that the radiated noise level of the forklift depends on the low frequency. Through the low frequency sound absorption improvement test and the standard test on the prototype, it shows that the level of prototype’s radiated sound power reduces by 1.75 dB(A), which demonstrates that a satisfactory effect on noise reduction is achieved. Finally, the effective noise reduction method proposed in this paper can also be tried and applied for different models of engineering vehicles and other working conditions.
Fundings: The work was supported by the Natural Science Foundation of Fujian Province (2018J01483), National Natural Science Foundation of China (12004136), China Postdoctoral Science Foundation (2019M662252) and Doctoral Scientific Research Foundation of Chengyi University College (CK17063).
Acknowledgments: The work was also supported by Outstanding Young Scientific Research Talents Cultivation Plan of Fujian Universities, and thanks to the engineering technology research institute of Xiamen XGMA Machinery Co., Ltd for providing test vehicle.
References
[1] Gupta A., Gupta A., Jain K., Gupta S. Noise pollution and impact on children health. India Journal of pediatrics, 85: 300-306,2018.
[2] Ahmadian H., Najafi G., Ghobadian B., Hassan-Beygi S.R., Hoseini S.S. Evaluation of the combustion-induced noise and vibration using coherence and wavelet coherence estimates in a diesel engine. International Journal of Engine Research, 1468087419878547, 2019.
[3] Lopez M.G., Sanchez L.P., Lozano H.M., Moreno L.N.O. Separation and Identification of Environmental Noise Signals Using Independent Component Analysis and Data Mining Techniques. Electronics, Robotics and Automotive Mechanics Conference (CERMA),Nov 15-18, 2011.
[4] Sun R.Z., Du H.Y., Zheng Y.G. Discriminative power of independent component analysis applied to an electronic nose. Measurement Science and Technology, 31: 035108,2020.
[5] Pamwani L., Shelke A. Damage quantification in moment resisting frame using phase space reconstructed from independent component sources. Structural Control & Health Monitoring, 26: e2438,2019.
[6] Cai X., Wang X., Huang Z.T., Wang F.H. Performance analysis of ICA in sensor array. Sensors, 16: 637-642,2016.
[7] Sompairac N., Nazarov P.V., Czerwinska U. et al. Independent component analysis for unraveling the complexity of cancer omics datasets. International Journal of Molecular Science, 20: 4414,2019.
[8] Haile M.A, Dykas B. Blind source separation for vibration-based diagnostics of rotorcraft bearings. Journal of Vibration and Control, 22: 3807-3820,2016.
[9] Li C.F., Liu L., Lei Y.M., et al Clustering for HSI hyperspectral image with weighted PCA and ICA. Journal of Intelligent & Fuzzy Systems, 32: 3729-3739,2017.
[10] Lopez-Pacheco M.G., Sanchez-Fernandez L.P., Molina-Lozano H. A method for environmental acoustic analysis improvement based on individual evaluation of common sources in urban areas. Science of the Total Environment, 468: 724-737,2014.
[11] Cheng W., Zhang Z.S., Zhu G.W., He Z.J. Noise source identification and localization of mechanical systems based on an enhanced independent component analysis. Journal of Vibration and Control, 22: 1128-1142,2016.
[12] Zhang Z.L., Pi Y.M., Sun Z.J. Independent component analysis based on denosing technology. Journal of the University of Electronic Science and Technology of China, 34: 296-299,2005.
[13] Hyvarinen A. 1999 The fixed-point algorithm and maximum likelihood estimation for independent component analysis. Neural Processing Letters, 10: 1-5,1999.
[14] Jiao W.D., Yang S.X., Qian S.X. Yan G.B. Method for recognition of independent sources of complex system under strong interferences. Chinese Journal of Mechanical Engineering, 42: 149-153,2009.
[15] Zhang X.X., Qiu T.S. Study on the indeterminacy of the statistical independent based on ICA methods. System Engineering and Electronics, 26: 556-559,2004.
[16] Wang J.L. Application of improved Quasi-Newton method to the massive image denoising. Multimedia Tools and Applications, 77: 12157-12170,2018.
[17] Han L., Li C.W., Guo S.L., Su X.W. Feature extraction method of bearing AE signal based on improved FAST-ICA and wavelet packet energy. Mechanical Systems and Signal Processing, 62-63: 91-99,2015.
[18] Mo C.X., Lu S.L. New method for fast elimination of uncertanities in ICA estimate based on spectrum similarity. Noise and Vibration Control, 5:102-104,2008.
[19] Hou L., Zhang E.L., Guo Y. Noise source determination for vehicle engine compartment based on a corrected fast independent component analysis. International Journal of Vehicle and Vibration, 12: 199-216,2016.
[20] Zhang E.L., Hou L., Yang W.P. Noise source idendification and experimental research of engine compartment of a forklift based on fast independent component analysis and scan & paint. Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Nov 13-15, Houston, 2015.
[21] Xu F., Li C.R., Jiang T.M. On the shaker simulation of wind-induced non-Gaussian random vibration. Shock and Vibration, 5450865,2016.
[22] Yoo C. Selection of mother wavelet for bivariate wavelet analysis. Journal of Korea Water Resources Assocition, 52: 905-916,2019.
[23] Qin Y., Xing J.F., Mao Y.F. Weak transient fault feature extraction based on an optimized Morlet wavelet and kurtosis. Measurement Science and Technology, 27: 085003,2016.
[24] Li L., Liu .PQ., Xing Y., Guo H. Time-frequency analysis of acoustic signals from a high-lift configuration with two wavelet functions. Applied Acoustics, 129: 155-160,2018.
[25] Wang X., Bi F.R., Liu .CW., Du X.F. Shao K. Blind source separation and identification of internal combustion engine noise based on independent component and wavelet analysis. International Conference on Electrical and Control Engineering, 113-116,2011.
[26] Guo T. Noise source identification and evaluation technology for forklift and its' application. Master degree thesis, Xiamen University, 2017.Document information
Published on 01/10/20
Accepted on 20/09/20
Submitted on 25/03/20
Volume 36, Issue 4, 2020
DOI: 10.23967/j.rimni.2020.09.007
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?