| (32 intermediate revisions by 3 users not shown) | |||
| Line 18: | Line 18: | ||
--> | --> | ||
| − | |||
==Resumen== | ==Resumen== | ||
| + | La generación de energía utilizando energía renovable como la energía eólica y solar depende del comportamiento del clima. Un pronóstico meteorológico preciso mejora la gestión de la operación de una red inteligente. Sin embargo, las condiciones ambientales varían con el tiempo y el espacio y, según la ubicación, tienen diferentes clasificaciones. Las condiciones ambientales varían con el tiempo y dependiendo del país, también los cambios entre el horario estándar, local y de verano pueden resultar en días de 23 h, para obtener días de 24 h. Las dos horas adyacentes se utilizan para calcular la hora que falta. En este artículo se aborda un modelo de regresión simbólica no lineal (RS) que se utiliza para hacer pronósticos de demanda anual. Este algoritmo es una evaluación con mediciones reales que crean modelos que se ajustan al pronóstico de carga de 28 estaciones meteorológicas. Las variables de aprendizaje son cargas de demanda y temperaturas; que se agrupan por horas para un intervalo de dos años. El algoritmo RS-DEEPSO se propone para mejorar el pronóstico. Esto se utiliza debido a sus cualidades evolutivas, autoadaptativas y la posibilidad de explorar nuevos escenarios en busca de lo óptimo. El pronóstico obtenido con el nuevo híbrido RS-DEEPSO tiene un error promedio por día inferior al 3,9% y por hora es inferior al 5,62% durante un período de 1 año. | ||
| − | + | '''Palabras Clave''': Pronóstico de demanda, optimización basada en ensamble, algoritmo metaheurístico, optimización mono-objetivo, regresión simbólica | |
| − | + | ||
| − | '''Palabras Clave''': | + | |
==Abstract== | ==Abstract== | ||
| Line 30: | Line 28: | ||
Power generation using renewable energy such as wind and solar energy depend on weather behavior. An accurate weather forecast improves the operation management of a Smart Grid. However, the environmental conditions vary with both time and space and, depending on the location have different classifications. The environmental conditions vary with time and depending on the country, also the changes between standard, local and summer time can result in days of 23 h, to obtain days of 24 h; the two adjacent hours are used to calculate the missing hour. In this paper is addressed a nonlinear symbolic regression (RS by its acronym in Spanish) model is used to make annual demand forecasts. This algorithm is assessment with real measurements creating models that conform to the load forecasting of 28 weather stations. The learning variables are loads of demand and temperatures; that are grouped by hours for a two-year time interval. The RS-DEEPSO algorithm is proposed to improve the forecast. This is used due to its evolutionary, self-adaptive qualities and the possibility of exploring new scenarios in search of optimum. The forecast obtained using the new hybrid RS-DEEPSO has an average error per day less than 3.9% and per hour is less than 5.62% during a period of 1 year. | Power generation using renewable energy such as wind and solar energy depend on weather behavior. An accurate weather forecast improves the operation management of a Smart Grid. However, the environmental conditions vary with both time and space and, depending on the location have different classifications. The environmental conditions vary with time and depending on the country, also the changes between standard, local and summer time can result in days of 23 h, to obtain days of 24 h; the two adjacent hours are used to calculate the missing hour. In this paper is addressed a nonlinear symbolic regression (RS by its acronym in Spanish) model is used to make annual demand forecasts. This algorithm is assessment with real measurements creating models that conform to the load forecasting of 28 weather stations. The learning variables are loads of demand and temperatures; that are grouped by hours for a two-year time interval. The RS-DEEPSO algorithm is proposed to improve the forecast. This is used due to its evolutionary, self-adaptive qualities and the possibility of exploring new scenarios in search of optimum. The forecast obtained using the new hybrid RS-DEEPSO has an average error per day less than 3.9% and per hour is less than 5.62% during a period of 1 year. | ||
| − | '''Keywords''': | + | '''Keywords''': Demand forecast, ensembled based optimization, metaheuristic algorithm, mono-objective optimization, symbolic regression |
| − | == | + | ==1. Introducción== |
Predecir el número óptimo de generadores que se despachan y la cantidad de potencia a generar para satisfacer la demanda de una red eléctrica, es uno de los retos dentro del control y planeación de los sistemas de energía eléctrica. La incursión de las redes inteligentes y las nuevas políticas gubernamentales promueven la penetración de la generación distribuida [1]. Las fuentes primarias de las energías renovables están normalmente distribuidas geográficamente [1]. Una planeación efectiva de la operación del despacho de energía debe incluir pronósticos a corto, mediano y largo plazo de la red eléctrica. | Predecir el número óptimo de generadores que se despachan y la cantidad de potencia a generar para satisfacer la demanda de una red eléctrica, es uno de los retos dentro del control y planeación de los sistemas de energía eléctrica. La incursión de las redes inteligentes y las nuevas políticas gubernamentales promueven la penetración de la generación distribuida [1]. Las fuentes primarias de las energías renovables están normalmente distribuidas geográficamente [1]. Una planeación efectiva de la operación del despacho de energía debe incluir pronósticos a corto, mediano y largo plazo de la red eléctrica. | ||
| Line 50: | Line 48: | ||
En la sección 2 se realiza el primer pronóstico utilizando estructuras de árbol del algoritmo RS no lineal híbrido y en la segunda parte el pronóstico es mejorado con el algoritmo DEEPSO. En la sección 3 se presenta un caso de estudio real para el pronóstico de demanda anual de 28 estaciones meteorológicas utilizando las dos etapas. Además, análisis comparativos del error son incluidos y se finaliza con las conclusiones. | En la sección 2 se realiza el primer pronóstico utilizando estructuras de árbol del algoritmo RS no lineal híbrido y en la segunda parte el pronóstico es mejorado con el algoritmo DEEPSO. En la sección 3 se presenta un caso de estudio real para el pronóstico de demanda anual de 28 estaciones meteorológicas utilizando las dos etapas. Además, análisis comparativos del error son incluidos y se finaliza con las conclusiones. | ||
| − | == | + | ==2. Materiales y métodos: pronóstico de demanda == |
| − | Para el pronóstico de demanda se proponen dos etapas tal como se muestra en la | + | Para el pronóstico de demanda se proponen dos etapas tal como se muestra en la [[#img-1|Figura 1]]. En la primera etapa se utiliza el algoritmo de regresión simbólica en el proceso de inferencia y en la segunda etapa se mejoran los resultados utilizando el algoritmo DEEPSO. |
| − | <div | + | <div id='img-1'></div> |
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | |
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Draft_Rivera_373381492-image1.png|350px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 1'''. Propuesta de pronóstico de demanda en 2 etapas | ||
| + | |} | ||
| − | |||
| − | === | + | ===2.1. Primera etapa: regresión simbólica en el proceso de inferencia=== |
| − | El algoritmo RS representa la evolución natural usando su propia programación genética [8]. Es decir, similar al principio Darwiniano evolucionan el cruce, los cromosomas y la mutación genética. Su esencia brinda la posibilidad de variar programas que forman parte de la población de soluciones. Esto permite encontrar un programa óptimo en menor tiempo. Algunos términos biológicos se utilizan en el algoritmo RS. El fenotipo se denomina al conjunto de rasgos que representan a un cromosoma en particular. La información necesaria para construir un nuevo organismo se denomina genotipo. Esta información se procesa con un cromosoma y se ejemplifica usando un programa de árbol ( | + | El algoritmo RS representa la evolución natural usando su propia programación genética [8]. Es decir, similar al principio Darwiniano evolucionan el cruce, los cromosomas y la mutación genética. Su esencia brinda la posibilidad de variar programas que forman parte de la población de soluciones. Esto permite encontrar un programa óptimo en menor tiempo. Algunos términos biológicos se utilizan en el algoritmo RS. El fenotipo se denomina al conjunto de rasgos que representan a un cromosoma en particular. La información necesaria para construir un nuevo organismo se denomina genotipo. Esta información se procesa con un cromosoma y se ejemplifica usando un programa de árbol ([[#img-1|Figura 1]]) [8]. Los programas de árbol se basan en regresión simbólica, por lo que es posible incluir conceptos de búsqueda basados en poblaciones [6]. |
| − | ====1 | + | ====2.1.1. Algoritmo de regresión simbólica ==== |
| − | El algoritmo de regresión simbólica, propuesto en [10], es una aplicación de un paradigma de computación evolutivo que intenta descubrir la forma funcional correcta de una expresión matemática con sus coeficientes numéricos que mejor se ajustan a un conjunto finito de datos. Esto significa que, mediante el uso de un conjunto de observaciones o datos experimentales de variables involucradas en un sistema, el algoritmo puede encontrar una expresión matemática o modelo que se ajuste a ellos con cierto grado de precisión, lo que permite el descubrimiento de relaciones entre variables, específicamente entre una variable dependiente ( | + | El algoritmo de regresión simbólica, propuesto en Langdon et al. [10], es una aplicación de un paradigma de computación evolutivo que intenta descubrir la forma funcional correcta de una expresión matemática con sus coeficientes numéricos que mejor se ajustan a un conjunto finito de datos. Esto significa que, mediante el uso de un conjunto de observaciones o datos experimentales de variables involucradas en un sistema, el algoritmo puede encontrar una expresión matemática o modelo que se ajuste a ellos con cierto grado de precisión, lo que permite el descubrimiento de relaciones entre variables, específicamente entre una variable dependiente (<math>y</math>) y otras independientes (<math>x</math>). El algoritmo se inicializa con una población de individuos compuesta por un único gen de estructura de árbol mediante el cual se codifica una expresión matemática. |
Así en algún grado, se ajusta a los valores de las variables referidas. En general, este grado o puntaje se calcula mediante el error de aproximación promedio, como el error cuadrático medio (RMSE) sobre el conjunto completo de observaciones. El resultado de este cálculo determina la probabilidad de que cada individuo participe en operaciones genéticas. Estas operaciones son la reproducción, la selección para obtener una nueva población, el cruce y la recombinación. Al implementar estas operaciones, es posible generar una nueva población cuyo desempeño se reevalúa para continuar el proceso de forma iterativa hasta que se alcance un criterio de terminación, que es el número máximo de generaciones definido por el usuario. | Así en algún grado, se ajusta a los valores de las variables referidas. En general, este grado o puntaje se calcula mediante el error de aproximación promedio, como el error cuadrático medio (RMSE) sobre el conjunto completo de observaciones. El resultado de este cálculo determina la probabilidad de que cada individuo participe en operaciones genéticas. Estas operaciones son la reproducción, la selección para obtener una nueva población, el cruce y la recombinación. Al implementar estas operaciones, es posible generar una nueva población cuyo desempeño se reevalúa para continuar el proceso de forma iterativa hasta que se alcance un criterio de terminación, que es el número máximo de generaciones definido por el usuario. | ||
| − | En última instancia, el modelo simbólico será el modelo que genere el menor grado de error de aproximación durante todo el proceso. Originalmente, el algoritmo de regresión simbólica considera cada modelo de solución individual o potencial como un solo gen o estructura de árbol que codifica una sola expresión matemática. Mientras tanto, en [10] | + | En última instancia, el modelo simbólico será el modelo que genere el menor grado de error de aproximación durante todo el proceso. Originalmente, el algoritmo de regresión simbólica considera cada modelo de solución individual o potencial como un solo gen o estructura de árbol que codifica una sola expresión matemática. Mientras tanto, en Langdon et al. [10] y Patelli [11] se presentan una modificación de este enfoque considerando a cada individuo como un conjunto de genes cuya combinación lineal ponderada genera el resultado de la inferencia tal como se muestra en la [[#img-2|Figura 2]]. |
| − | <div | + | <div id='img-1'></div> |
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | |
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Draft_Rivera_373381492-image2.png|600px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 2'''. Ejemplo de un individuo multi-gen | ||
| + | |} | ||
| − | |||
| − | La estimación dada por el individuo se calcula como se indica en las ecuaciones (1) y (2), donde ( | + | La estimación dada por el individuo se calcula como se indica en las ecuaciones (1) y (2), donde (<math>x_i</math>), <math>i=\{1,2,3\}</math> son valores de variables independientes, (<math>\alpha_i</math>) son factores de peso y <math> (\hat y)</math> es el valor de inferencia |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 83: | Line 89: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math display="inline">\overset{\mbox{ˆ}}{y}={\alpha }_0+{\alpha }_1gen_1+ | + | | <math display="inline">\overset{\mbox{ˆ}}{y}={\alpha }_0+{\alpha }_1gen_1+{\alpha }_2 gen_2 +{\alpha }_3gen_3</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (1) | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) | ||
| Line 93: | Line 99: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\overset{\mbox{ˆ}}{y}={\alpha }_0+{\alpha }_1\left(sin(x_1)- | + | | <math>\overset{\mbox{ˆ}}{y}={\alpha }_0+{\alpha }_1\left(sin(x_1)- x_2\right)+{\alpha }_2tan(7.3x_2)+{\alpha }_3\left(x_2\left(x_3- x_1\right)\right)</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (2) | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) | ||
|} | |} | ||
| − | + | La tarea subsiguiente en la fase de evaluación del algoritmo implica encontrar el conjunto de factores de ponderación que generan la expresión ajustando las observaciones registradas con la menor discrepancia posible del valor real. En Langdon et al. [10] y Patelli [11], esta búsqueda se estima utilizando el algoritmo de mínimos cuadrados ordinarios (MCO). Esta técnica propone la expresión mostrada en la ecuación (3) como una solución. De acuerdo con la ecuación, se construye una matriz como resultado de evaluar el conjunto de observaciones en los genes de cada individuo. (Esta matriz tiene tantas filas como el número de observaciones y tantas columnas como el número de genes individuales más uno). Si bien es un vector que contiene los valores reales de la variable dependiente [12] | |
| − | La tarea subsiguiente en la fase de evaluación del algoritmo implica encontrar el conjunto de factores de ponderación que generan la expresión ajustando las observaciones registradas con la menor discrepancia posible del valor real. En [10] | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 111: | Line 116: | ||
|} | |} | ||
| − | + | Al tener los valores del vector <math>\alpha</math>, el valor de inferencia, (<math>\hat y</math>), dado por el individuo, se puede calcular como se indica en la ecuación (4), y el rendimiento se define como el error (<math>e</math>) (calculado como la suma de cuadrados), de acuerdo con la ecuación (5) | |
| − | Al tener los valores del vector | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 134: | Line 138: | ||
|} | |} | ||
| + | ====2.1.2. Propuesta del algoritmo de regresión simbólica no lineal híbrida==== | ||
| − | + | En esta sección se utiliza el término ''regresión de crestas no lineales'', que permite representar la configuración de una matriz con una función lineal, gaussiana o polinomial. Este artículo propone establecer una relación no lineal entre los genes con una regresión de crestas no lineales. En Searson et al. [13] y Hii et al. [14], se propone asignar un número máximo de genes o estructuras de árboles que codifiquen expresiones matemáticas para cada individuo de la población. | |
| − | En | + | El algoritmo de regresión simbólica no lineal híbrida se desarrolla en dos etapas inicialización y repetición. En la etapa de inicialización se definen longitud máxima y mínima de individuos, tamaño de la población, estructuras de árbol, funciones de árbol y tipo de selección. En la etapa de repetición se configura la regresión de crestas no lineal, los individuos que se codifican, se mide el error y se seleccionan los mejores individuos de acuerdo con la [[#img-3|Figura 3]]. |
| − | + | <div id='img-3'></div> | |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Draft_Rivera_373381492-image8.png|310px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 3'''. Algoritmo de representación simbólica no lineal | ||
| + | |} | ||
| − | === | + | ===2.2. Segunda etapa: con el algoritmo de optimización DEEPSO=== |
El algoritmo DEEPSO es utilizado para mejorar el primer pronóstico. Este es un hibrido conformado por algoritmos EA, PSO y DE. Estos métodos promueven la búsqueda del óptimo en la dirección global correcta [7]. El algoritmo de optimización de enjambre de partículas evolutiva (EPSO por sus siglas en inglés) mejora las cualidades de solución del EA y el PSO. El algoritmo PSO se basa en la selección Darwiniana para promover progreso hacia el óptimo correcto. El método EPSO tiene una interpretación evolutiva completa, de hecho es remplazada la operación de recombinación por una nueva llamada movimiento de partículas [15]. | El algoritmo DEEPSO es utilizado para mejorar el primer pronóstico. Este es un hibrido conformado por algoritmos EA, PSO y DE. Estos métodos promueven la búsqueda del óptimo en la dirección global correcta [7]. El algoritmo de optimización de enjambre de partículas evolutiva (EPSO por sus siglas en inglés) mejora las cualidades de solución del EA y el PSO. El algoritmo PSO se basa en la selección Darwiniana para promover progreso hacia el óptimo correcto. El método EPSO tiene una interpretación evolutiva completa, de hecho es remplazada la operación de recombinación por una nueva llamada movimiento de partículas [15]. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
El algoritmo EPSO en una iteración dada, considera un conjunto de partículas. Las partículas representan posibles soluciones. El EPSO tiene las siguientes características: | El algoritmo EPSO en una iteración dada, considera un conjunto de partículas. Las partículas representan posibles soluciones. El EPSO tiene las siguientes características: | ||
| Line 162: | Line 168: | ||
:* SELECCIÓN: Por un torneo estocástico las mejores partículas sobreviven para formar una nueva generación [7]. | :* SELECCIÓN: Por un torneo estocástico las mejores partículas sobreviven para formar una nueva generación [7]. | ||
| − | El movimiento de partículas esta dado por una partícula | + | |
| + | El movimiento de partículas esta dado por una partícula <math>X_i</math> y una nueva partícula <math>X_i^{nuevo}</math> tal como se expresa en la ecuación (6). La velocidad de la partícula se define en la ecuación (7), donde <math>b_G</math> es el mejor punto encontrado del enjambre en la línea de vida directa de la partícula, <math>b_i</math> es el conjunto de partículas y A, B, C son las matrices diagonales definidas al principio del proceso [1,7]. El mejor global <math>b_G</math> es aleatoriamente perturbado con una distribución normal como <math>b_G^* = b_G +\tau' N(0,1)</math>, donde <math>\tau '</math> es un parámetro de aprendizaje | ||
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 184: | Line 191: | ||
|} | |} | ||
| − | + | El algoritmo DE esta basado en parámetros fijos, los cuales reclaman un proceso auto-adaptativo para estos parámetros. Él genera una nueva solución a partir de un individuo existente, donde <math>X_{r1}^k</math> y <math>X_{r2}^k</math> son un par de partículas distintas descritas en la ecuación (8). La recombinación asegura la diversidad, la selección es elitista basada en la media de cada competencia. El EPSO es un algoritmo auto-adaptativo. Así se propone el algoritmo DEEPSO para mejorar los algoritmos DE y EPSO como se muestra en la ecuación (9). El conjunto P pertenece a la generación actual [7] | |
| − | El algoritmo DE esta basado en parámetros fijos, los cuales reclaman un proceso auto-adaptativo para estos parámetros. Él genera una nueva solución a partir de un individuo existente, donde | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 206: | Line 212: | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (9) | | style="width: 5px;text-align: right;white-space: nowrap;" | (9) | ||
|} | |} | ||
| − | |||
Definidos los algoritmos RS y DEEPSO se formula el caso de estudio. | Definidos los algoritmos RS y DEEPSO se formula el caso de estudio. | ||
| − | == | + | ==3. Caso de estudio, resultados y discusión== |
| − | Para la evaluación de la metodología se tomaron los datos de una ciudad de los Estados Unidos donde se instalaron 28 estaciones meteorológicas para tomar mediciones de la demanda de energía [2]. Para entrenamiento de la red se utilizó el año 2005 y 2006. El año 2005 se tomó con 365 y el año 2006 con 364 días para un total de 729 días. El día faltante se utilizó para el año 2007, el cual tiene 366 días. La clasificación por periodos de la demanda se presenta en la | + | Para la evaluación de la metodología se tomaron los datos de una ciudad de los Estados Unidos donde se instalaron 28 estaciones meteorológicas para tomar mediciones de la demanda de energía [2]. Para entrenamiento de la red se utilizó el año 2005 y 2006. El año 2005 se tomó con 365 y el año 2006 con 364 días para un total de 729 días. El día faltante se utilizó para el año 2007, el cual tiene 366 días. La clasificación por periodos de la demanda se presenta en la [[#img-4|Figura 4]]. Esta clasificación consiste en tomar los datos suministrados por 28 estaciones para cada día y predecir la demanda del mismo día. El cálculo se realizó por separado para las 24 horas en los que se calcularon 729 cargas de demanda [2]. |
| − | [[Image:Draft_Rivera_373381492-image13.png|600px]] | + | <div id='img-4'></div> |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Draft_Rivera_373381492-image13.png|600px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 4'''. Categorización por periodos de la demanda | ||
| + | |} | ||
| − | |||
| − | Otro factor a tener en cuenta son las condiciones ambientales que varían con el tiempo y, según el país, tienen diferentes clasificaciones. Según la temporada, se clasifican como hora estándar, horario de verano y hora local. La hora estándar sincroniza los diferentes relojes ubicados en la misma región; estos se basan en los meridianos. El horario de verano consiste en ajustar las horas de luz de acuerdo con la actividad humana; el ajuste se realiza una hora antes del comienzo de la primavera y una hora más tarde en otoño. La hora local significa una hora calculada para la región en particular. Estos cambios de horas fueron previstos en el pronóstico de cargas. Entonces, para los veranos en los que hay 23 horas, la hora faltante se calcula utilizando las dos horas adyacentes [2]. Las 28 temperaturas tomadas de estaciones de los Estados Unidos se muestran en la | + | Otro factor a tener en cuenta son las condiciones ambientales que varían con el tiempo y, según el país, tienen diferentes clasificaciones. Según la temporada, se clasifican como hora estándar, horario de verano y hora local. La hora estándar sincroniza los diferentes relojes ubicados en la misma región; estos se basan en los meridianos. El horario de verano consiste en ajustar las horas de luz de acuerdo con la actividad humana; el ajuste se realiza una hora antes del comienzo de la primavera y una hora más tarde en otoño. La hora local significa una hora calculada para la región en particular. Estos cambios de horas fueron previstos en el pronóstico de cargas. Entonces, para los veranos en los que hay 23 horas, la hora faltante se calcula utilizando las dos horas adyacentes [2]. Las 28 temperaturas tomadas de estaciones de los Estados Unidos se muestran en la [[#img-5|Figura 5]]. |
| + | |||
| + | <div id='img-5'></div> | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Figuraaa5.jpg|600px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 5'''. Condiciones meteorológicas registradas de 28 estaciones | ||
| + | |} | ||
| − | |||
| − | + | El pronóstico de demanda se realiza utilizando regresión simbólica en la subsección A y se mejora con el algoritmo DEEPSO sub-sección B. | |
Los datos son analizados en Matlab versión 2019b, en los cálculos se utiliza una memoria para el procesamiento de datos alrededor 208 MB. Por ejemplo en el algoritmo RS, en la memoria se almacenan paquetes del pronóstico anterior y el actual. Mientras en el algoritmo DEEPSO son almacenados las variables de velocidad de la partícula, percepción del gradiente local y cooperación. Además de contar con una rutina para autoajustar los pesos para estás tres variables. Por lo tanto, el algoritmo DEEPSO tiene un mayor costo computacional. | Los datos son analizados en Matlab versión 2019b, en los cálculos se utiliza una memoria para el procesamiento de datos alrededor 208 MB. Por ejemplo en el algoritmo RS, en la memoria se almacenan paquetes del pronóstico anterior y el actual. Mientras en el algoritmo DEEPSO son almacenados las variables de velocidad de la partícula, percepción del gradiente local y cooperación. Además de contar con una rutina para autoajustar los pesos para estás tres variables. Por lo tanto, el algoritmo DEEPSO tiene un mayor costo computacional. | ||
| − | + | ===3.1. Primera etapa con regresión simbólica RS=== | |
| − | + | El algoritmo de regresión simbólica RS no lineal es utilizado para el aprendizaje de algoritmos genéticos, la inferencia se muestra en la [[#img-6|Figura 6]]. En la hora 7 se calcula el error de entrenamiento para 729 días, el cual tiene un error absoluto de 9,6%. El objetivo representa el pronóstico de demanda real y la inferencia los resultados que arrojan la regresión simbólica no lineal. | |
| − | + | <div id='img-6'></div> | |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Figuraaa6.jpg|600px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 6'''. Cálculo de inferencia del error para 28 estaciones | ||
| + | |} | ||
| − | |||
| − | Una vez entrenada la población de individuos, se realiza el pronóstico de demanda anual para 366 días a las 7 a.m. presentado en la | + | Una vez entrenada la población de individuos, se realiza el pronóstico de demanda anual para 366 días a las 7 a.m. presentado en la [[#img-7|Figura 7]], el error por inferencia es igual a 16,2%. |
| − | [[Image: | + | <div id='img-7'></div> |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Figuraaa7.jpg|600px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 7'''. Pronóstico de demanda con RS | ||
| + | |} | ||
| − | |||
| − | [[ | + | La demanda de 2 años es utilizada para el aprendizaje del algoritmo RS. La [[#img-8|Figura 8]] muestra el error porcentual obtenido por cada hora. El error tiende a incrementarse para la hora 18 a un 20,28%. El error medio por horas es equivalente al 12,7%. |
| − | < | + | <div id='img-8'></div> |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Draft_Rivera_373381492-image17-c.png|550px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 8'''. Error de aprendizaje por horas con el algoritmo RS | ||
| + | |} | ||
| − | |||
| − | [[ | + | El pronóstico es realizado para un año, el error porcentual por hora de pronóstico se presenta en la [[#img-9|Figura 9]], el mayor error pertenece a la hora 18 con un máximo de 27,74%. El error medio del pronóstico es del 19,46%. |
| − | < | + | <div id=img-9></div> |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Figuraaa9.jpg|550px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 9'''. Error de pronóstico por horas con el algoritmo RS | ||
| + | |} | ||
| − | ===2. Segunda etapa con DEEPSO=== | + | ===3.2. Segunda etapa con DEEPSO=== |
| − | La predicción tiene un error del 16,2 %. Al utilizar el algoritmo DEEPSO, el error se disminuyó al 2,7 %, como se muestra en la | + | La predicción tiene un error del 16,2%. Al utilizar el algoritmo DEEPSO, el error se disminuyó al 2,7%, como se muestra en la [[#img-10|Figura 10]]. |
| − | [[Image: | + | <div id=img-10></div> |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Figuraaa10.jpg|600px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 10'''. Pronóstico de demanda con RS-DEEPSO | ||
| + | |} | ||
| − | |||
| − | [[ | + | El error del algoritmo RS se mejora utilizando el algoritmo DEEPSO. Dos efectos se evidencian: el primero es una reducción del error porcentual a un valor medio de 3,9% y el segundo efecto está relacionado con suavizar picos en la curva de pronóstico del error como se muestra en la [[#img-11|Figura 11]]. El error máximo para pronóstico de demanda intradia (por horas) es del 5,62% a las 8 a.m usando el RS-DEEPSO. El horizonte de pronóstico es de 366 días. |
| − | < | + | <div id=img-11></div> |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Figuraaa11.jpg|550px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 11'''. Error de pronóstico por horas con el algoritmo RS-DEEPSO | ||
| + | |} | ||
| − | El indicador de la | + | |
| + | El indicador de la ecuación (10) permite conocer la reducción del error en porcentaje. | ||
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 269: | Line 319: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <span id='_Hlk32661484'></span> <math>R\%=\frac{e_{RS}-e_{DEEPSO}}{e_{RS}}\ast 100\%</math> | + | | <span id='_Hlk32661484'></span> <math>R\% =\frac{e_{RS}-e_{DEEPSO}}{e_{RS}}\ast 100\%</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (10) | | style="width: 5px;text-align: right;white-space: nowrap;" | (10) | ||
| Line 275: | Line 325: | ||
| − | El error se reduce en la segunda etapa con el algoritmo RS-DEEPSO. La reducción del error promedio es de un 77,7 %, la distribución del error se muestra en la | + | El error se reduce en la segunda etapa con el algoritmo RS-DEEPSO. La reducción del error promedio es de un 77,7%, la distribución del error se muestra en la [[#img-12|Figura 12]]. En cada hora el error se reduce con pequeñas fluctuaciones alrededor de 77,7%, con excepción de la hora 8, donde la reducción del error es alrededor del 48%. |
| − | [[Image:Draft_Rivera_373381492-image22-c.png| | + | <div id=img-12></div> |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Draft_Rivera_373381492-image22-c.png|550px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 12'''. Reducción del error de pronóstico por horas con el algoritmo RS-DEEPSO | ||
| + | |} | ||
| − | + | ==4. Conclusión== | |
| − | + | ||
| − | == | + | |
Pronósticos con alta incertidumbre de la demanda energía dan como resultados un desabastecimiento de la demanda o sobrecostos. Así, mediante pronósticos de demanda con una baja incertidumbre se contribuye a optimizar la planeación operativa de las redes eléctricas. Este artículo se presentó y evaluó el algoritmo RS-DEEPSO para el pronóstico de demanda anual de energía por horas. El algoritmo RS no lineal hibrido con sus más resientes modificaciones fue comparado con un nuevo hibrido el algoritmo RS-DEEPSO. | Pronósticos con alta incertidumbre de la demanda energía dan como resultados un desabastecimiento de la demanda o sobrecostos. Así, mediante pronósticos de demanda con una baja incertidumbre se contribuye a optimizar la planeación operativa de las redes eléctricas. Este artículo se presentó y evaluó el algoritmo RS-DEEPSO para el pronóstico de demanda anual de energía por horas. El algoritmo RS no lineal hibrido con sus más resientes modificaciones fue comparado con un nuevo hibrido el algoritmo RS-DEEPSO. | ||
| − | El desempeño de los dos algoritmos se evaluó entrenándolos mediante registros de mediciones de temperatura de 28 estaciones meteorológicas durante 2 años con el fin de predecir la demanda para un tercer año. Como resultado, el RS-DEEPSO redujo el error en 77,7 % respecto al RS no lineal hibrido, con un error promedio en el pronóstico por días inferior al 3,9 % y un error promedio máximo para las 8 a.m de 5,62 %. | + | El desempeño de los dos algoritmos se evaluó entrenándolos mediante registros de mediciones de temperatura de 28 estaciones meteorológicas durante 2 años con el fin de predecir la demanda para un tercer año. Como resultado, el RS-DEEPSO redujo el error en 77,7% respecto al RS no lineal hibrido, con un error promedio en el pronóstico por días inferior al 3,9% y un error promedio máximo para las 8 a.m de 5,62%. |
| − | + | ||
==Acknowledgements== | ==Acknowledgements== | ||
| − | The authors would like to thank the Cyted Network: RED IBEROAMERICANA PARA EL DESARROLLO Y LA INTEGRACION DE PEQUENOS GENERADORES EOLICOS(MICRO-EOLO) for the continued support during | + | Los autores quieren agradecer a Cyted Network: RED IBEROAMERICANA PARA EL DESARROLLO Y LA INTEGRACION DE PEQUENOS GENERADORES EOLICOS (MICRO-EOLO) por el continuo apoyo durante el desarrollo de este trabajo. |
| + | <!--The authors would like to thank the Cyted Network: RED IBEROAMERICANA PARA EL DESARROLLO Y LA INTEGRACION DE PEQUENOS GENERADORES EOLICOS(MICRO-EOLO) for the continued support during the development of this work.--> | ||
==Referencias== | ==Referencias== | ||
| Line 296: | Line 350: | ||
<div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | ||
| − | [1] | + | [1] García-Guarín J., Rivera S., Rodriguez H. Revisión REI: realidad en Colombia y expectativas. V Encuentro Int. Innovación Tecnológica, 5:1–7, 2018. |
| − | + | ||
| − | + | ||
| − | [ | + | [2] Hong T., Wang P., White L. Weather station selection for electric load forecasting. Int. J. Forecast., 31(2): 286–295, 2015. |
| − | [ | + | [3] Vargas S., Rodriguez D., Rivera S. Mathematical formulation and numerical validation of uncertainty costs for controllable loads. Rev. Int. Métodos Numéricos para Cálculo y Diseño en Ing., 35:16, 2019. |
| − | [ | + | [4] Chen Y., Hong W., Shen W. Electric load forecasting based on a least squares support vector machine with fuzzy time series and global harmony search algorithm. Energies, 9(2):70-79, 2016. |
| − | [ | + | [5] Choi S., Pellen A., Masson V. How does daylight saving time affect electricity demand? An answer using aggregate data from a natural experiment in Western Australia. Energy Econ., 66:247–260, 2017. |
| − | [ | + | [6] Manrique-Naranjo S., Guzman M., Rivera S. Hybrid inference algorithm by combining genetic programming methods and nonlinear regression techniques. Far East Journal of Experimental and Theoretical Artificial Intelligence, 7(1):1-27, 2018. |
| − | [ | + | [7] Miranda V., Alves R. Differential evolutionary particle swarm optimization (deepso): A successful hybrid. IEEE BRICS Congress on Computational Intelligence and 11th Brazilian Congress on Computational Intelligence, 368–374, 2013. |
| − | [ | + | [8] Pérez E., Bautista D., Acevedo F., Pimentel J. Programación genética aplicada al pronóstico de viento en la región del istmo de tehuantepec. 2° Congr. Int. Energías Renov., 1:1–11, 2016. |
| − | [ | + | [9] Kronberger G., Kommenda M., Lughofer E., Saminger-Platz S., Promberger A., Nickel F., Winkler S., Affenzeller M. Using robust generalized fuzzy modeling and enhanced symbolic regression to model tribological systems. Applied Soft Computing, 69:610-624, 2018. |
| − | [ | + | [10] Langdon W., Poli R., McPhee N., Koza J. Genetic programming: An introduction and tutorial, with a survey of techniques and applications. Computational Intelligence: A Compendium. Studies in Computational Intelligence, Vol. 115, Springer, Berlin, 2008. |
| − | [ | + | [11] Patelli A. Genetic programming techniques for nonlinear systems identification. Iasi, Rum. Ed. Politeh., 22(16):1–243, 2011. |
| − | [ | + | [12] Vanneschi L. Improving genetic programming for the prediction of pharmacokinetic parameters. Memetic Comput., 6(4):255–262, 2014. |
| − | [ | + | [13] Searson D., Leahy D., Willis M. GPTIPS: an open source genetic programming toolbox for multigene symbolic regression. Proc. Int. Multiconference Eng. Comput. Sci., 1(1):77–80, 2010. |
| − | [ | + | [14] Hii C., Searson D., Willis M. Evolving toxicity models using multigene symbolic regression and multiple objectives. Int. J. Mach. Learn. Comput., 1(1):22-30, 2011. |
| + | [15] Miranda V., Fonseca N. EPSO-evolutionary particle swarm optimization, a new algorithm with applications in power systems. IEEE/PES Transm. Distrib. Conf. Exhib., 2(1):745–750, 2002. | ||
| + | <!-- | ||
[[Image:Draft_Rivera_373381492-image23-c.jpeg|center|102px]] | [[Image:Draft_Rivera_373381492-image23-c.jpeg|center|102px]] | ||
| Line 338: | Line 392: | ||
'''Sergio Raul Rivera Rodriguez '''is currently an associate professor of electrical engineering at the National University of Colombia where he specializes in smart grids. He got a Fulbright fellowship as a research scholar at the University of Florida. He was a postdoctoral researcher at the Massachusetts Institute of Technology and the within the LIINES at the Masdar Institute of Science & Technology. Prior to his postdoctoral fellowships, he was working General Motors as a Senior Process Engineer in the Manufacturing Engineering Area. Meanwhile, he was a professor of power systems in the District University where he taught courses in the reliability of power systems and electricity markets. His received his Ph.D. from the Electric Energy Institute at the national University of San Jan in Argentina. There, he proposed a methodology for short-term investment decisions in electric distribution networks considering uncertainties in planning parameters. | '''Sergio Raul Rivera Rodriguez '''is currently an associate professor of electrical engineering at the National University of Colombia where he specializes in smart grids. He got a Fulbright fellowship as a research scholar at the University of Florida. He was a postdoctoral researcher at the Massachusetts Institute of Technology and the within the LIINES at the Masdar Institute of Science & Technology. Prior to his postdoctoral fellowships, he was working General Motors as a Senior Process Engineer in the Manufacturing Engineering Area. Meanwhile, he was a professor of power systems in the District University where he taught courses in the reliability of power systems and electricity markets. His received his Ph.D. from the Electric Energy Institute at the national University of San Jan in Argentina. There, he proposed a methodology for short-term investment decisions in electric distribution networks considering uncertainties in planning parameters. | ||
| + | --> | ||
Latest revision as of 10:34, 24 August 2020
Resumen
La generación de energía utilizando energía renovable como la energía eólica y solar depende del comportamiento del clima. Un pronóstico meteorológico preciso mejora la gestión de la operación de una red inteligente. Sin embargo, las condiciones ambientales varían con el tiempo y el espacio y, según la ubicación, tienen diferentes clasificaciones. Las condiciones ambientales varían con el tiempo y dependiendo del país, también los cambios entre el horario estándar, local y de verano pueden resultar en días de 23 h, para obtener días de 24 h. Las dos horas adyacentes se utilizan para calcular la hora que falta. En este artículo se aborda un modelo de regresión simbólica no lineal (RS) que se utiliza para hacer pronósticos de demanda anual. Este algoritmo es una evaluación con mediciones reales que crean modelos que se ajustan al pronóstico de carga de 28 estaciones meteorológicas. Las variables de aprendizaje son cargas de demanda y temperaturas; que se agrupan por horas para un intervalo de dos años. El algoritmo RS-DEEPSO se propone para mejorar el pronóstico. Esto se utiliza debido a sus cualidades evolutivas, autoadaptativas y la posibilidad de explorar nuevos escenarios en busca de lo óptimo. El pronóstico obtenido con el nuevo híbrido RS-DEEPSO tiene un error promedio por día inferior al 3,9% y por hora es inferior al 5,62% durante un período de 1 año.
Palabras Clave: Pronóstico de demanda, optimización basada en ensamble, algoritmo metaheurístico, optimización mono-objetivo, regresión simbólica
Abstract
Power generation using renewable energy such as wind and solar energy depend on weather behavior. An accurate weather forecast improves the operation management of a Smart Grid. However, the environmental conditions vary with both time and space and, depending on the location have different classifications. The environmental conditions vary with time and depending on the country, also the changes between standard, local and summer time can result in days of 23 h, to obtain days of 24 h; the two adjacent hours are used to calculate the missing hour. In this paper is addressed a nonlinear symbolic regression (RS by its acronym in Spanish) model is used to make annual demand forecasts. This algorithm is assessment with real measurements creating models that conform to the load forecasting of 28 weather stations. The learning variables are loads of demand and temperatures; that are grouped by hours for a two-year time interval. The RS-DEEPSO algorithm is proposed to improve the forecast. This is used due to its evolutionary, self-adaptive qualities and the possibility of exploring new scenarios in search of optimum. The forecast obtained using the new hybrid RS-DEEPSO has an average error per day less than 3.9% and per hour is less than 5.62% during a period of 1 year.
Keywords: Demand forecast, ensembled based optimization, metaheuristic algorithm, mono-objective optimization, symbolic regression
1. Introducción
Predecir el número óptimo de generadores que se despachan y la cantidad de potencia a generar para satisfacer la demanda de una red eléctrica, es uno de los retos dentro del control y planeación de los sistemas de energía eléctrica. La incursión de las redes inteligentes y las nuevas políticas gubernamentales promueven la penetración de la generación distribuida [1]. Las fuentes primarias de las energías renovables están normalmente distribuidas geográficamente [1]. Una planeación efectiva de la operación del despacho de energía debe incluir pronósticos a corto, mediano y largo plazo de la red eléctrica.
Los pronósticos ayudan a impulsar el desarrollo económico y mejorar la fiabilidad de los sistemas [2] y son una herramienta utilizada para minimizar los costos de incertidumbre en la generación tanto tradicional como de renovables. Dentro de las fuentes renovables más utilizadas está la energía solar y eólica. Sin embargo, la generación de energía a partir de estas fuentes es influenciada por las condiciones climáticas las cuales varían en el tiempo y en el espacio, ocasionando intermitencia en la generación. Este fenómeno, no deseado, causa sobrecostos debido a la sobreestimación o la subestimación de la potencia inyectada por la generación renovable [3]. Para considerar estas condiciones durante la predicción se han propuesto diversas técnicas [2].
Dentro de las técnicas mediante las cuales se busca mejorar la predicción de la demanda está la lógica difusa, redes neuronales computacionales (NN por sus siglas en inglés) y las técnicas de aprendizaje automático [4]. Estas técnicas se basan en tomar un historial de carga y, con base a esto, realizar la predicción. El historial de carga se toma para un horizonte de predicción a mediano plazo, que está influenciada por las horas pico, las cargas promedio y las vacaciones [5].
En este articulo una metodología de pronóstico a mediano plazo utilizando regresión simbólica (RS) [6] y optimización de enjambre de partículas evolutivas diferenciales (DEEPSO por sus siglas en inglés) es abordada. La unión entre estos dos algoritmos RS-DEEPSO se propone como un método hibrido novedoso [7], el cual está inspirado en la evolución biológica y poblacional [8].
La regresión simbólica (RS) es un híbrido que resulta de la combinación de computación evolutiva y regresión no lineal. Los modelos no lineales están fundamentados en regresiones simples basadas en estadísticas e inteligencia artificial, entre los que se encuentran las redes neuronales siendo el más utilizado. La regresión simbólica brinda la posibilidad de utilizar funciones para la creación del árbol (el árbol relaciona genes con expresiones aritméticas (-,+,*,/) y trigonométricas (seno, tangente)). La población se organiza por jerarquías y genera una nueva población basada en el principio de la recombinación genética [8].
Métodos de optimización son seleccionados debido a sus aplicaciones en pronósticos de carga. Por ejemplo, el algoritmo RS es planteado de acuerdo con las siguientes comparaciones con otros métodos. Primero como ilustración, el algoritmo NN posee una compleja estructura que dificulta el debate sobre el comportamiento general; más bien, se debe confiar en estimaciones empíricas como el error de validación cruzada. Segundo, los modelos de regresión lineal simples son insuficientes para estimar las métricas de interés en los sistemas paramétricos; en general, las técnicas de RS no lineal más avanzadas funcionaron mejor. Tercero, el modelo difuso y RS con adaptaciones tienen una precisión predictiva y complejidades similares. Por lo tanto, el análisis comparativo en un estudio de caso entre NN, modelos de regresión lineal simple, RS no lineal y modelo difuso demostraron que el algoritmo RS no lineal realizaba predicciones con un menor o igual error [9].
Otro método de optimización seleccionado en esta investigación es el algoritmo DEEPSO, el cual es un híbrido que toma características de algoritmos evolutivos (EA por sus siglas en inglés), optimización de enjambre de partículas (PSO por sus siglas en inglés) y evolución diferencial (DE por sus siglas en inglés). En esta propuesta, el algoritmo DEEPSO es seleccionado por presentar un rendimiento superior al algoritmo EPSO [7]. Por lo tanto, DEEPSO tiene características evolutivas, autoadaptativas y poder exploratorio con características de mutación y recombinación, las cuales se utilizan para mejorar el pronóstico obtenido con la RS.
En la sección 2 se realiza el primer pronóstico utilizando estructuras de árbol del algoritmo RS no lineal híbrido y en la segunda parte el pronóstico es mejorado con el algoritmo DEEPSO. En la sección 3 se presenta un caso de estudio real para el pronóstico de demanda anual de 28 estaciones meteorológicas utilizando las dos etapas. Además, análisis comparativos del error son incluidos y se finaliza con las conclusiones.
2. Materiales y métodos: pronóstico de demanda
Para el pronóstico de demanda se proponen dos etapas tal como se muestra en la Figura 1. En la primera etapa se utiliza el algoritmo de regresión simbólica en el proceso de inferencia y en la segunda etapa se mejoran los resultados utilizando el algoritmo DEEPSO.

|
| Figura 1. Propuesta de pronóstico de demanda en 2 etapas |
2.1. Primera etapa: regresión simbólica en el proceso de inferencia
El algoritmo RS representa la evolución natural usando su propia programación genética [8]. Es decir, similar al principio Darwiniano evolucionan el cruce, los cromosomas y la mutación genética. Su esencia brinda la posibilidad de variar programas que forman parte de la población de soluciones. Esto permite encontrar un programa óptimo en menor tiempo. Algunos términos biológicos se utilizan en el algoritmo RS. El fenotipo se denomina al conjunto de rasgos que representan a un cromosoma en particular. La información necesaria para construir un nuevo organismo se denomina genotipo. Esta información se procesa con un cromosoma y se ejemplifica usando un programa de árbol (Figura 1) [8]. Los programas de árbol se basan en regresión simbólica, por lo que es posible incluir conceptos de búsqueda basados en poblaciones [6].
2.1.1. Algoritmo de regresión simbólica
El algoritmo de regresión simbólica, propuesto en Langdon et al. [10], es una aplicación de un paradigma de computación evolutivo que intenta descubrir la forma funcional correcta de una expresión matemática con sus coeficientes numéricos que mejor se ajustan a un conjunto finito de datos. Esto significa que, mediante el uso de un conjunto de observaciones o datos experimentales de variables involucradas en un sistema, el algoritmo puede encontrar una expresión matemática o modelo que se ajuste a ellos con cierto grado de precisión, lo que permite el descubrimiento de relaciones entre variables, específicamente entre una variable dependiente () y otras independientes (). El algoritmo se inicializa con una población de individuos compuesta por un único gen de estructura de árbol mediante el cual se codifica una expresión matemática.
Así en algún grado, se ajusta a los valores de las variables referidas. En general, este grado o puntaje se calcula mediante el error de aproximación promedio, como el error cuadrático medio (RMSE) sobre el conjunto completo de observaciones. El resultado de este cálculo determina la probabilidad de que cada individuo participe en operaciones genéticas. Estas operaciones son la reproducción, la selección para obtener una nueva población, el cruce y la recombinación. Al implementar estas operaciones, es posible generar una nueva población cuyo desempeño se reevalúa para continuar el proceso de forma iterativa hasta que se alcance un criterio de terminación, que es el número máximo de generaciones definido por el usuario.
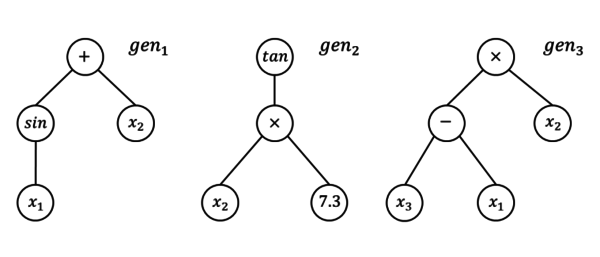
En última instancia, el modelo simbólico será el modelo que genere el menor grado de error de aproximación durante todo el proceso. Originalmente, el algoritmo de regresión simbólica considera cada modelo de solución individual o potencial como un solo gen o estructura de árbol que codifica una sola expresión matemática. Mientras tanto, en Langdon et al. [10] y Patelli [11] se presentan una modificación de este enfoque considerando a cada individuo como un conjunto de genes cuya combinación lineal ponderada genera el resultado de la inferencia tal como se muestra en la Figura 2.
|
| Figura 2. Ejemplo de un individuo multi-gen |
La estimación dada por el individuo se calcula como se indica en las ecuaciones (1) y (2), donde (), son valores de variables independientes, () son factores de peso y es el valor de inferencia
|
|
(1) |
|
|
(2) |
La tarea subsiguiente en la fase de evaluación del algoritmo implica encontrar el conjunto de factores de ponderación que generan la expresión ajustando las observaciones registradas con la menor discrepancia posible del valor real. En Langdon et al. [10] y Patelli [11], esta búsqueda se estima utilizando el algoritmo de mínimos cuadrados ordinarios (MCO). Esta técnica propone la expresión mostrada en la ecuación (3) como una solución. De acuerdo con la ecuación, se construye una matriz como resultado de evaluar el conjunto de observaciones en los genes de cada individuo. (Esta matriz tiene tantas filas como el número de observaciones y tantas columnas como el número de genes individuales más uno). Si bien es un vector que contiene los valores reales de la variable dependiente [12]
|
|
(3) |
Al tener los valores del vector , el valor de inferencia, (), dado por el individuo, se puede calcular como se indica en la ecuación (4), y el rendimiento se define como el error () (calculado como la suma de cuadrados), de acuerdo con la ecuación (5)
|
|
(4) |
|
|
(5) |
2.1.2. Propuesta del algoritmo de regresión simbólica no lineal híbrida
En esta sección se utiliza el término regresión de crestas no lineales, que permite representar la configuración de una matriz con una función lineal, gaussiana o polinomial. Este artículo propone establecer una relación no lineal entre los genes con una regresión de crestas no lineales. En Searson et al. [13] y Hii et al. [14], se propone asignar un número máximo de genes o estructuras de árboles que codifiquen expresiones matemáticas para cada individuo de la población.
El algoritmo de regresión simbólica no lineal híbrida se desarrolla en dos etapas inicialización y repetición. En la etapa de inicialización se definen longitud máxima y mínima de individuos, tamaño de la población, estructuras de árbol, funciones de árbol y tipo de selección. En la etapa de repetición se configura la regresión de crestas no lineal, los individuos que se codifican, se mide el error y se seleccionan los mejores individuos de acuerdo con la Figura 3.

|
| Figura 3. Algoritmo de representación simbólica no lineal |
2.2. Segunda etapa: con el algoritmo de optimización DEEPSO
El algoritmo DEEPSO es utilizado para mejorar el primer pronóstico. Este es un hibrido conformado por algoritmos EA, PSO y DE. Estos métodos promueven la búsqueda del óptimo en la dirección global correcta [7]. El algoritmo de optimización de enjambre de partículas evolutiva (EPSO por sus siglas en inglés) mejora las cualidades de solución del EA y el PSO. El algoritmo PSO se basa en la selección Darwiniana para promover progreso hacia el óptimo correcto. El método EPSO tiene una interpretación evolutiva completa, de hecho es remplazada la operación de recombinación por una nueva llamada movimiento de partículas [15].
El algoritmo EPSO en una iteración dada, considera un conjunto de partículas. Las partículas representan posibles soluciones. El EPSO tiene las siguientes características:
- REPLICACIÓN: Cada partícula es replicada r veces.
- MUTACIÓN: Cada partícula tiene su peso w mutado.
- REPRODUCCIÓN: Cada partícula mutada genera un descendiente según la regla de movimiento de partículas.
- EVALUACIÓN: Cada descendiente se evalúa su aptitud.
- SELECCIÓN: Por un torneo estocástico las mejores partículas sobreviven para formar una nueva generación [7].
El movimiento de partículas esta dado por una partícula y una nueva partícula tal como se expresa en la ecuación (6). La velocidad de la partícula se define en la ecuación (7), donde es el mejor punto encontrado del enjambre en la línea de vida directa de la partícula, es el conjunto de partículas y A, B, C son las matrices diagonales definidas al principio del proceso [1,7]. El mejor global es aleatoriamente perturbado con una distribución normal como , donde es un parámetro de aprendizaje
|
|
(6) |
|
|
(7) |
El algoritmo DE esta basado en parámetros fijos, los cuales reclaman un proceso auto-adaptativo para estos parámetros. Él genera una nueva solución a partir de un individuo existente, donde y son un par de partículas distintas descritas en la ecuación (8). La recombinación asegura la diversidad, la selección es elitista basada en la media de cada competencia. El EPSO es un algoritmo auto-adaptativo. Así se propone el algoritmo DEEPSO para mejorar los algoritmos DE y EPSO como se muestra en la ecuación (9). El conjunto P pertenece a la generación actual [7]
|
|
(8) |
|
|
(9) |
Definidos los algoritmos RS y DEEPSO se formula el caso de estudio.
3. Caso de estudio, resultados y discusión
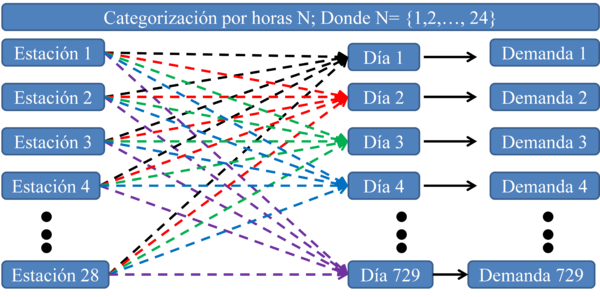
Para la evaluación de la metodología se tomaron los datos de una ciudad de los Estados Unidos donde se instalaron 28 estaciones meteorológicas para tomar mediciones de la demanda de energía [2]. Para entrenamiento de la red se utilizó el año 2005 y 2006. El año 2005 se tomó con 365 y el año 2006 con 364 días para un total de 729 días. El día faltante se utilizó para el año 2007, el cual tiene 366 días. La clasificación por periodos de la demanda se presenta en la Figura 4. Esta clasificación consiste en tomar los datos suministrados por 28 estaciones para cada día y predecir la demanda del mismo día. El cálculo se realizó por separado para las 24 horas en los que se calcularon 729 cargas de demanda [2].
|
| Figura 4. Categorización por periodos de la demanda |
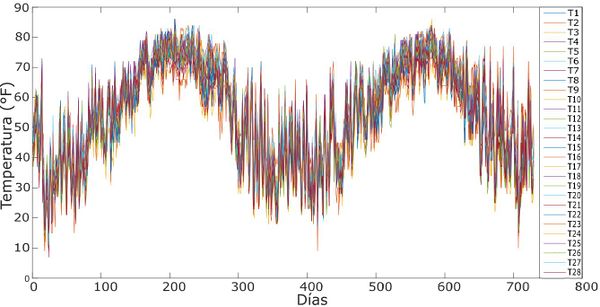
Otro factor a tener en cuenta son las condiciones ambientales que varían con el tiempo y, según el país, tienen diferentes clasificaciones. Según la temporada, se clasifican como hora estándar, horario de verano y hora local. La hora estándar sincroniza los diferentes relojes ubicados en la misma región; estos se basan en los meridianos. El horario de verano consiste en ajustar las horas de luz de acuerdo con la actividad humana; el ajuste se realiza una hora antes del comienzo de la primavera y una hora más tarde en otoño. La hora local significa una hora calculada para la región en particular. Estos cambios de horas fueron previstos en el pronóstico de cargas. Entonces, para los veranos en los que hay 23 horas, la hora faltante se calcula utilizando las dos horas adyacentes [2]. Las 28 temperaturas tomadas de estaciones de los Estados Unidos se muestran en la Figura 5.
|
| Figura 5. Condiciones meteorológicas registradas de 28 estaciones |
El pronóstico de demanda se realiza utilizando regresión simbólica en la subsección A y se mejora con el algoritmo DEEPSO sub-sección B.
Los datos son analizados en Matlab versión 2019b, en los cálculos se utiliza una memoria para el procesamiento de datos alrededor 208 MB. Por ejemplo en el algoritmo RS, en la memoria se almacenan paquetes del pronóstico anterior y el actual. Mientras en el algoritmo DEEPSO son almacenados las variables de velocidad de la partícula, percepción del gradiente local y cooperación. Además de contar con una rutina para autoajustar los pesos para estás tres variables. Por lo tanto, el algoritmo DEEPSO tiene un mayor costo computacional.
3.1. Primera etapa con regresión simbólica RS
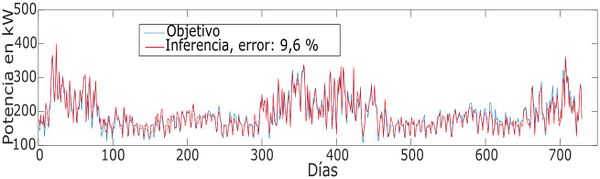
El algoritmo de regresión simbólica RS no lineal es utilizado para el aprendizaje de algoritmos genéticos, la inferencia se muestra en la Figura 6. En la hora 7 se calcula el error de entrenamiento para 729 días, el cual tiene un error absoluto de 9,6%. El objetivo representa el pronóstico de demanda real y la inferencia los resultados que arrojan la regresión simbólica no lineal.
|
| Figura 6. Cálculo de inferencia del error para 28 estaciones |
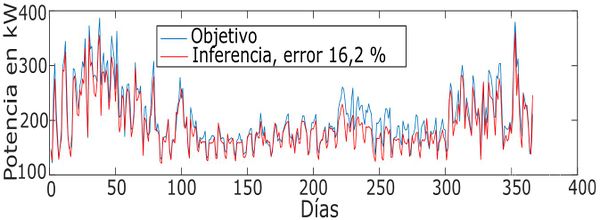
Una vez entrenada la población de individuos, se realiza el pronóstico de demanda anual para 366 días a las 7 a.m. presentado en la Figura 7, el error por inferencia es igual a 16,2%.
|
| Figura 7. Pronóstico de demanda con RS |
La demanda de 2 años es utilizada para el aprendizaje del algoritmo RS. La Figura 8 muestra el error porcentual obtenido por cada hora. El error tiende a incrementarse para la hora 18 a un 20,28%. El error medio por horas es equivalente al 12,7%.

|
| Figura 8. Error de aprendizaje por horas con el algoritmo RS |
El pronóstico es realizado para un año, el error porcentual por hora de pronóstico se presenta en la Figura 9, el mayor error pertenece a la hora 18 con un máximo de 27,74%. El error medio del pronóstico es del 19,46%.

|
| Figura 9. Error de pronóstico por horas con el algoritmo RS |
3.2. Segunda etapa con DEEPSO
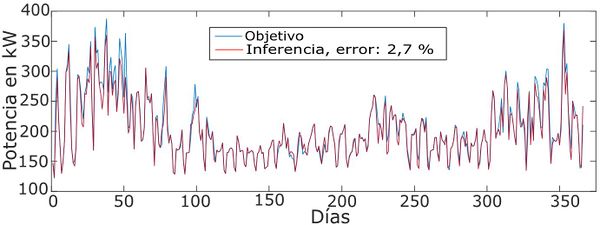
La predicción tiene un error del 16,2%. Al utilizar el algoritmo DEEPSO, el error se disminuyó al 2,7%, como se muestra en la Figura 10.
|
| Figura 10. Pronóstico de demanda con RS-DEEPSO |
El error del algoritmo RS se mejora utilizando el algoritmo DEEPSO. Dos efectos se evidencian: el primero es una reducción del error porcentual a un valor medio de 3,9% y el segundo efecto está relacionado con suavizar picos en la curva de pronóstico del error como se muestra en la Figura 11. El error máximo para pronóstico de demanda intradia (por horas) es del 5,62% a las 8 a.m usando el RS-DEEPSO. El horizonte de pronóstico es de 366 días.

|
| Figura 11. Error de pronóstico por horas con el algoritmo RS-DEEPSO |
El indicador de la ecuación (10) permite conocer la reducción del error en porcentaje.
|
|
(10) |
El error se reduce en la segunda etapa con el algoritmo RS-DEEPSO. La reducción del error promedio es de un 77,7%, la distribución del error se muestra en la Figura 12. En cada hora el error se reduce con pequeñas fluctuaciones alrededor de 77,7%, con excepción de la hora 8, donde la reducción del error es alrededor del 48%.

|
| Figura 12. Reducción del error de pronóstico por horas con el algoritmo RS-DEEPSO |
4. Conclusión
Pronósticos con alta incertidumbre de la demanda energía dan como resultados un desabastecimiento de la demanda o sobrecostos. Así, mediante pronósticos de demanda con una baja incertidumbre se contribuye a optimizar la planeación operativa de las redes eléctricas. Este artículo se presentó y evaluó el algoritmo RS-DEEPSO para el pronóstico de demanda anual de energía por horas. El algoritmo RS no lineal hibrido con sus más resientes modificaciones fue comparado con un nuevo hibrido el algoritmo RS-DEEPSO.
El desempeño de los dos algoritmos se evaluó entrenándolos mediante registros de mediciones de temperatura de 28 estaciones meteorológicas durante 2 años con el fin de predecir la demanda para un tercer año. Como resultado, el RS-DEEPSO redujo el error en 77,7% respecto al RS no lineal hibrido, con un error promedio en el pronóstico por días inferior al 3,9% y un error promedio máximo para las 8 a.m de 5,62%.
Acknowledgements
Los autores quieren agradecer a Cyted Network: RED IBEROAMERICANA PARA EL DESARROLLO Y LA INTEGRACION DE PEQUENOS GENERADORES EOLICOS (MICRO-EOLO) por el continuo apoyo durante el desarrollo de este trabajo.
Referencias
[1] García-Guarín J., Rivera S., Rodriguez H. Revisión REI: realidad en Colombia y expectativas. V Encuentro Int. Innovación Tecnológica, 5:1–7, 2018.
[2] Hong T., Wang P., White L. Weather station selection for electric load forecasting. Int. J. Forecast., 31(2): 286–295, 2015.
[3] Vargas S., Rodriguez D., Rivera S. Mathematical formulation and numerical validation of uncertainty costs for controllable loads. Rev. Int. Métodos Numéricos para Cálculo y Diseño en Ing., 35:16, 2019.
[4] Chen Y., Hong W., Shen W. Electric load forecasting based on a least squares support vector machine with fuzzy time series and global harmony search algorithm. Energies, 9(2):70-79, 2016.
[5] Choi S., Pellen A., Masson V. How does daylight saving time affect electricity demand? An answer using aggregate data from a natural experiment in Western Australia. Energy Econ., 66:247–260, 2017.
[6] Manrique-Naranjo S., Guzman M., Rivera S. Hybrid inference algorithm by combining genetic programming methods and nonlinear regression techniques. Far East Journal of Experimental and Theoretical Artificial Intelligence, 7(1):1-27, 2018.
[7] Miranda V., Alves R. Differential evolutionary particle swarm optimization (deepso): A successful hybrid. IEEE BRICS Congress on Computational Intelligence and 11th Brazilian Congress on Computational Intelligence, 368–374, 2013.
[8] Pérez E., Bautista D., Acevedo F., Pimentel J. Programación genética aplicada al pronóstico de viento en la región del istmo de tehuantepec. 2° Congr. Int. Energías Renov., 1:1–11, 2016.
[9] Kronberger G., Kommenda M., Lughofer E., Saminger-Platz S., Promberger A., Nickel F., Winkler S., Affenzeller M. Using robust generalized fuzzy modeling and enhanced symbolic regression to model tribological systems. Applied Soft Computing, 69:610-624, 2018.
[10] Langdon W., Poli R., McPhee N., Koza J. Genetic programming: An introduction and tutorial, with a survey of techniques and applications. Computational Intelligence: A Compendium. Studies in Computational Intelligence, Vol. 115, Springer, Berlin, 2008.
[11] Patelli A. Genetic programming techniques for nonlinear systems identification. Iasi, Rum. Ed. Politeh., 22(16):1–243, 2011.
[12] Vanneschi L. Improving genetic programming for the prediction of pharmacokinetic parameters. Memetic Comput., 6(4):255–262, 2014.
[13] Searson D., Leahy D., Willis M. GPTIPS: an open source genetic programming toolbox for multigene symbolic regression. Proc. Int. Multiconference Eng. Comput. Sci., 1(1):77–80, 2010.
[14] Hii C., Searson D., Willis M. Evolving toxicity models using multigene symbolic regression and multiple objectives. Int. J. Mach. Learn. Comput., 1(1):22-30, 2011.
[15] Miranda V., Fonseca N. EPSO-evolutionary particle swarm optimization, a new algorithm with applications in power systems. IEEE/PES Transm. Distrib. Conf. Exhib., 2(1):745–750, 2002.
Document information
Published on 16/07/20
Accepted on 30/06/20
Submitted on 17/03/20
Volume 36, Issue 3, 2020
DOI: 10.23967/j.rimni.2020.07.001
Licence: CC BY-NC-SA license