| Line 1,412: | Line 1,412: | ||
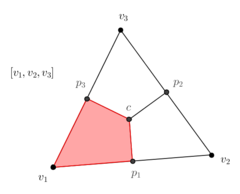
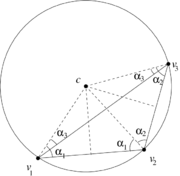
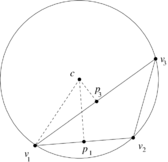
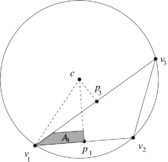
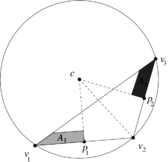
In order to understand how local DEC assigns area weights to vertices differently from FEML, let us consider the obtuse triangle shown in Figure [[#img-8|8]]. Let <math display="inline">p_1,p_2,p_3</math> be the middle points of the segments <math display="inline">[v_1,v_2],[v_1,v_3],[v_2,v_3]</math> respectively. As shown in Figure [[#img-9|9]], the triangle <math display="inline">[v_1,p_3,c]</math> lies completely outside of the triangle <math display="inline">[v_1,v_2,v_3]</math>. Geometrically, this implies that its area must be assigned a negative sign, which is confirmed by the determinant formulas of Subsection [[#6.1 The discrete Hodge star quantities revisited|6.1]]. On the other hand, the triangle <math display="inline">[v_1,p_1,c]</math> will have positive area. Thus, their sum gives us the area <math display="inline">A_1</math> in Figure [[#img-9|9]]. | In order to understand how local DEC assigns area weights to vertices differently from FEML, let us consider the obtuse triangle shown in Figure [[#img-8|8]]. Let <math display="inline">p_1,p_2,p_3</math> be the middle points of the segments <math display="inline">[v_1,v_2],[v_1,v_3],[v_2,v_3]</math> respectively. As shown in Figure [[#img-9|9]], the triangle <math display="inline">[v_1,p_3,c]</math> lies completely outside of the triangle <math display="inline">[v_1,v_2,v_3]</math>. Geometrically, this implies that its area must be assigned a negative sign, which is confirmed by the determinant formulas of Subsection [[#6.1 The discrete Hodge star quantities revisited|6.1]]. On the other hand, the triangle <math display="inline">[v_1,p_1,c]</math> will have positive area. Thus, their sum gives us the area <math display="inline">A_1</math> in Figure [[#img-9|9]]. | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | <div id='img-9'></div> |
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" | ||
|- | |- | ||
| − | |[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle03a-eps-converted-to.png|168px|]] | + | |style="padding:10px;"|[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle03a-eps-converted-to.png|168px|]] |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | |[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle04a-eps-converted-to.png|168px|]] | + | |style="padding:10px;"|[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle04a-eps-converted-to.png|168px|]] |
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | |[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle05a-eps-converted-to.png|168px|Area weight assigned to ]] | + | |style="padding:10px;"|[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle05a-eps-converted-to.png|168px|Area weight assigned to ]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figure 9:''' Area weight assigned to | + | | colspan="1" style="padding-bottom:10px;"| '''Figure 9:''' Area weight assigned to |
|} | |} | ||
| + | |||
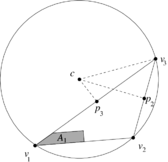
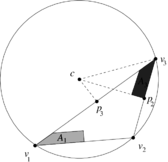
The area <math display="inline">A_3</math> is computed similarly, where the triangle <math display="inline">[p_3,v_3,c]</math> is assigned negative area (see Figure [[#img-10|10]]). | The area <math display="inline">A_3</math> is computed similarly, where the triangle <math display="inline">[p_3,v_3,c]</math> is assigned negative area (see Figure [[#img-10|10]]). | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | <div id='img-10'></div> |
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" | ||
|- | |- | ||
| − | |[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle06a-eps-converted-to.png|168px|]] | + | |style="padding:10px;"|[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle06a-eps-converted-to.png|168px|]] |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | |[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle07a-eps-converted-to.png|168px|]] | + | |style="padding:10px;"|[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle07a-eps-converted-to.png|168px|]] |
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | |[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle08a-eps-converted-to.png|168px| | + | |style="padding:10px;"|[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle08a-eps-converted-to.png|168px|]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figure 10:''' Area weight assigned to | + | | colspan="1" style="padding-bottom:10px;"| '''Figure 10:''' Area weight assigned to |
|} | |} | ||
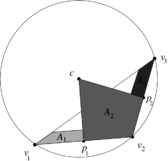
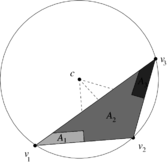
| − | Note that for <math display="inline">A_2</math>, the two triangles <math display="inline">[p_1,v_2,c]</math> and <math display="inline">[v_2,p_2,c]</math> both have positive areas ( | + | Note that for <math display="inline">A_2</math>, the two triangles <math display="inline">[p_1,v_2,c]</math> and <math display="inline">[v_2,p_2,c]</math> both have positive areas (Figure [[#img-11|11]]). |
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | <div id='img-11'></div> |
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" | ||
|- | |- | ||
| − | |[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle09a-eps-converted-to.png|168px|]] | + | |style="padding:10px;"|[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle09a-eps-converted-to.png|168px|]] |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | |[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle10a-eps-converted-to.png|168px|]] | + | |style="padding:10px;"|[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle10a-eps-converted-to.png|168px|]] |
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | |[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle11a-eps-converted-to.png|168px|Area weight assigned to ]] | + | |style="padding:10px;"|[[Image:Esqueda_et_al_2020a-NonWellCenteredTriangle11a-eps-converted-to.png|168px|Area weight assigned to ]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figure 11:''' Area weight assigned to | + | | colspan="1" style="padding-bottom:10px;"| '''Figure 11:''' Area weight assigned to |
|} | |} | ||
Revision as of 13:02, 11 May 2020
Abstract
We present a local formulation for 2D Discrete Exterior Calculus (DEC) similar to that of the Finite Element Method (FEM), which allows a natural treatment of material heterogeneity (assigning material properties element by element). It also allows us to deduce, in a principled manner, anisotropic fluxes and the DEC discretization of the pullback of 1-forms by the anisotropy tensor, i.e. we deduce the discrete action of the anisotropy tensor on primal 1-forms. Due to the local formulation, the computational cost of DEC is similar to that of the Finite Element Method with Linear interpolating functions (FEML). The numerical DEC solutions to the anisotropic Poisson equation show numerical convergence, are very close to those of FEML on fine meshes and are slightly better than those of FEML on coarse meshes.
1. Introduction
The theory of Discrete Exterior Calculus (DEC) is a relatively recent discretization [8] of the classical theory of Exterior Differential Calculus developed by E. Cartan [3], which is a fundamental tool in Differential Geometry and Topology. The aim of DEC is to solve partial differential equations preserving their geometrical and physical features as much as possible. There are only a few papers about implementions of DEC to solve certain PDEs, such as the Darcy flow and Poisson's equation [9], the Navier-Stokes equations [10], the simulation of elasticity, plasticity and failure of isotropic materials [5], some comparisons with the finite differences and finite volume methods on regular flat meshes [7], as well as applications in digital geometry processing [4].
In this paper, we describe a local formulation of DEC which is reminiscent of that of the Finite Element Method (FEM). Indeed, once the local systems of equations have been established, they can be assembled into a global linear system. This local formulation is also efficient and helpful in understanding various features of DEC that can otherwise remain unclear if one is dealing dealing with an entire mesh. Besides, we believe the local description to DEC will be accesible to a wide readership. We will, therefore, take a local approach when recalling all the objects required by 2D DEC [6]. Our main results are the following:
- We present a local formulation of DEC analogous to that of FEM, which allows a natural treatment of heterogeneous material properties assigned to subdomains (element by element) and eliminates the need of dealing with it through ad hoc modifications of the global discrete Hodge star operator.
- Guided by the local formulation, we deduce a natural way to approximate the flux/gradient-vector of a discretized function, as well as the anisotropic flux vector. We carry out a comparison of the formulas defining the flux in both DEC and Finite Element Method with linear interpolation functions (FEML).
- In order to understand how to discretize the anisotropic Poisson equation, we develop the discretization of the pull-back operator of 1-forms under an arbitrary linear trasformation or tensor. The pull-back operator is one of the basic ingredients in Exterior Differential Calculus in the smooth setting and is essential in all of its applications in Topology [bott-Tu]. We discretize the pullback operator on primal 1-forms induced by an arbitrary tensor using Whitney interpolation (the Whitney map). The Whitney interpolation forms were introduced by Hassler Whitney in 1957 (see [12] p. 139) and Bossavit [1] explained their relevance in “mixed methods” of finite elements. To our knowledge, this is the first time that the discrete version of this operator is presented in the DEC literature. This has allowed us to discretize, in a principled manner, the anisotropic heat equation.
- We carry out an analytic comparison of the DEC and FEML local formulations of the anisotropic Poisson equation.
- We present three numerical examples of the approximate solutions to the stationary anisotropic Poisson equation on different domains using DEC and FEML. The numerical DEC-solutions exhibit numerical convergence (see the error measurement tables) and a competitive performance, as well as a computational cost similar to that of FEML. In fact, the numerical solutions with both methods on fine meshes are identical, and DEC shows a slightly better performance than FEML on coarse meshes.
The paper is organized as follows. In Section 2, we describe the local versions of the discrete derivative operator, the dual mesh, the discrete Hodge star operator and the meaning of a continuous 1-form on the plane. In Section 3, we deduce the discretization of the pullback operator on primal 1-forms. In Section 4, we deduce the natural way of computing flux vectors in DEC (which turns out to be equivalent to the FEML result), as well as the anisotropic flux vectors. In Section 5, we present the local DEC formulation of the 2D anisotropic Poisson equation and compare it with the local system of FEML, proving that the diffusion terms are identical in both schemes, while the source terms are differentl due to a different area-weight assignment for the nodes. In Section 6, we re-examine the geometry of some of the local DEC quantities. In Section 7, we present and compare numerical examples of DEC and FEML approximate solutions to the 2D anisotropic Poisson equation on different domains with meshes of various resolutions. In Section 8, we summarize the contributions of this paper.
2. Preliminaries on DEC from a local viewpoint
In this section, we will recall the basic operators of Dicrete Exterior Calculus restricting ourselves to a mesh made up of one simplex/triangle. The local results we derive in the paper can be assembled, just as in the Finite elemnt Method, due to the additivity of both differentiation and integration.
Let us consider a primal mesh made up of a single (positively oriented) triangle with vertices .
|
| Figure 1. Triangle |
Such a mesh has
- one oriented 2-dimensional face
|
|
- three oriented 1-dimensional edges
|
|
- and three 0-dimensional vertices
|
|
2.1 Boundary operator
There is a well known boundary operator
|
|
(1) |
which describes the boundary of the triangle as an alternated sum of its ordered oriented edges , and .
Similarly, one can compute the boundary of each edge
|
If we consider
- the symbol as a basis vector of a 1-dimensional vector space,
- the symbols , , as an ordered basis of a 3-dimensional vector space,
- the symbols , , as an ordered basis of a 3-dimensional vector space,
then the map (1), which sends the oriented triangle to a sum of its oriented edges, is represented by the matrix
|
|
while the map (2), which sends the oriented edges to sums of their oriented vertices, is represented by the matrix
|
|
2.2 Discrete derivative
It has been argued that the DEC discretization of the differential of a function is given by the transpose of the matrix of the boundary operator on edges (see [8,6]). More precisely, suppose we have a function discretized by its values at the vertices
|
|
Its discrete derivative, according to DEC, is
|
|
Indeed, such differences are rough approximations of the directional derivatives of along the oriented edges. For instance, is a rough approximation of the directional derivative of at in the direction of the vector , i.e.
|
|
It is precisely in this sense that, according to DEC,
- the value is assigned to the edge ,
- the value is assigned to the edge ,
- and the value is assigned to the edge .
Let
|
|
2.3 Dual mesh
The dual mesh of the primal mesh consisting of a single triangle is constructured as follows:
- To the 2-dimensional triangular face will correspond the 0-dimensional point given by the circumcenter of the triangle.
|
| Figure 2. Circumcenter |
- To the 1-dimensional edge will correspond the 1-dimensional straight line segment joining the midpoint of the edge to the circumcenter . Similarly for the other edges.
|
| Figure 3. Dual segment |
- To the 0-dimensional vertex/node will correspond the oriented -dimensional quadrilateral .
|
| Figure 4. Dual quadrilateral |
2.4 Discrete Hodge star
For the Poisson equation in 2D, we need two matrices: one relating original edges to dual edges, and another relating vertices to dual cells.
- The discrete Hodge star map applied to the discrete differential of a discretized function is given as follows:
- the value assigned to the edge is changed to the new value
|
|
assigned to the segment ;
- the value assigned to the edge is changed to the new value
|
|
assigned to the edge .
- the value assigned to the edge is changed to the new value
|
|
assigned to the segment ;
In other words,
|
|
- Similarly, the discrete Hodge star map on values on vertices is given as follows:
- the value assigned to the vertex is changed to the new value
|
|
assigned to the quadrilateral ;
- the value assigned to the vertex is changed to the new value
|
|
assigned to the quadrilateral ;
- the value assigned to the vertex is changed to the new value
|
|
assigned to the quadrilateral .
In other words,
|
|
2.5 Continuous 1-forms
A differential 1-form on can be thought of as a function whose arguments are a point in and a vector in , i.e.
|
|
and which is linear on the vector argument.
The dot product of allows us to see continuous 1-forms in a more familiar form as vector fields in the following way: If is a vector field on , at each point we can consider the 1-form
|
|
where . On the other hand, from a continuos 1-form we can build a vector field as follows
|
|
where
|
|
2.5.1 Pullback of a conitnuous 1-form
Given a tensor (a linear transformation) and the vector field associated to a 1-form as above, consider the vector field . For any vector , the value of the corresponding continuous 1-form is given by the product
|
|
which is the value of the 1-form called the pullback of by the tensor .
2.5.2 Discretization of continuous 1-forms
In order to produce a primal 1-form from such a continuous 1-form we need to inegrate it along the edges of the mesh (the de Rham map). In our local description, this produces a collection of 3 numbers associated to the 3 oriented edges of the triangle, i.e. for the oriented edge joining to we have
|
|
This is equivalent to calculating the line integral (circulation) of the corresponding vector field along the path , , parametrizing the edge
|
|
3. Pullback operator on primal 1-forms
In Section 2, we dealt with the primal discretization of a continuous 1-form. Now we wish to understand the pullback of a primal 1-form. In order to do this, we will interpolate a primal 1-form using the Whitney interpolation forms to produce a continuous 1-form (Whitney map) to which we can apply the pullback operator by a tensor (linear transformation), and then intergrate along the edges (de Rham map).
The Whitney interpolation forms were introduced by Whitney in 1957 [12], and Bossavit [1] explained their relevance to “mixed methods” of finite elements. For the sake of simplicity, we will only define the Whitney 0 and 1-forms.
First consider the Finite Element linear basis functions (or Whitney interpolation functions)
|
and their differentials
|
The Whitney interpolation 1-forms are
|
These differential 1-forms are such that, along the edge
|
|
i.e. or .
Now, suppose we have a primal 1-form given on our triangle by the collection of numbers
|
|
We form a continuous 1-form as follows
|
|
which is such that, for
|
|
Now we will calculate
|
|
for an arbitrary linear transformation
|
|
Let
|
|
and
|
|
As it turns out,
|
|
where
|
|
Anyhow, these quantities are areas of the parallelograms formed by one fixed edge of the original triangle and one edge transformed by .
Thus, we have that the induced transformation on primal 1-forms is
|
|
(6) |
When the material is isotropic, i.e. is a constant multiple of the identity matrix, we get a constant multiple of the identity matrix above as discrete pull-back operator.
4. Flux and anisotropy
In this section, we deduce the DEC formulae for the local flux, the local anisotropic flux and the local anisotropy operator for primal 1-forms.
4.1 The flux in local DEC
We wish to find a natural construction for the discrete flux (discrete gradient vector) of a discrete function. Recall from Vector Calculus that the directional derivative of a differentiable function at a point in the direction of is defined by
|
|
Thus, we have three Vector Calculus identities
|
|
As in subsection 2.2, the rough approximations to directional derivatives of a function in the directions of the (oriented) edges are given as follows
|
|
Thus, if we want to find a discrete gradient vector of at the point , we need to solve the equations
|
If
|
|
then
|
|
Now, if we were to find a discrete gradient vector of at the point , we need to solve the equations
|
The vectors solving these equations is actually equal to . Indeed, consider
|
|
so that
|
|
(10) |
Thus, adding up (7) and (9) we get
|
|
(11) |
Subtracting (8) from (10) we get
|
|
(12) |
Since and are linearly independent and the two inner products in (11) and (12) vanish,
|
|
Analogously, the corresponding gradient vector of at the vertex is equal to . This means that the three approximate gradient vectors at the three vertices coincide, i.e. we have a unique discrete flux vector on the given element. Note that the discrete flux satisfies
|
|
This means that the primal 1-form discretizing can be obtained by performing the dot products of the discrete flux vector with the vectors given by the triangle's oriented edges.
4.1.1 Comparison of DEC and FEML local fluxes
The local flux (gradient) of in FEML is given by
|
|
where and are the basis functions given in (3). Explicitly
|
|
where
|
|
is the area of the triangle, so that the FEML flux is given by
|
|
and we can see that it coincides with the DEC flux.
4.2 The anisotropic flux vector in local DEC
We will now discuss how to discretize anisotropy in 2D DEC. Let denote the symmetric anisotropy tensor
|
|
and recall the anisotropic Poisson equation
|
|
First recall that, in Exterior Differential Calculus, for any ,
|
|
where is the pullback of by .
Since we already have a discrete candidate for on the given element, the product of the matrix and gives us a candidate for the anisptropic flux vector on such an element
|
|
In order to produce a primal 1-form from , all we have to do is assume that is constant on the given triangle and take dot products with the edges of the triangle, i.e.
|
|
Nevertheless, in order to better understand the structure of the local system (as in FEML), it is desirable to have a factorization of the result as a matrix product
|
|
where the matrix is a real matrix depending on the geometry of the triangle and the matrix , and such that it is a multiple of the identity matrix when the domain is isotropic. In order to do this, we will use the discretization of the pullback opertator of Exterior Differential Calculus for arbitrary 1-forms from Section 3. Thus, using (6), is the following matrix where we have set , i.e.
|
|
where
|
|
4.2.1 Geometric interpretation of the entries of
Consider the following figure, where denotes the anti-clockwise rotation
|
|

|
| Figure 5. Geometric interpretation of the entries of the anisotropy tensor discretization |
We have
|
|
where is the area of the red triangle. Thus, the numbers are quotients of areas of transformed triangles divided by the area of the original triangle.
5. Anisotropic Poisson equation in 2D
In this section, we describe the local DEC discretization of the 2D anisotropic Poisson equation and compare it to that of FEML.
5.1 Local DEC discretization of the 2D anisotropic Poisson equation
The anisotropic Poisson equation reads as follows
|
|
where and are two functions on a certain domain in and is the anisotropy tensor. In terms of the exterior derivative and the Hodge star operator it reads as follows
|
|
where and . Following the discretization of the discretized divergence operator [6], the corresponding local DEC discretization of the anisotropic Poisson equation is
|
|
or equivalently
|
|
(13) |
In order to simplify the notation, consider the lengths and areas defined in the Figure 6.
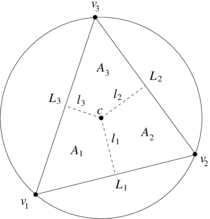
| |
| colspan="1" style="padding-bottom:10px;" | Figure 6 Triangle |
Now, the discretized equation (13) looks as follows:
|
|
The diffusive term matrix is actually symmetric (see Subsection 5.3.1).
5.2 Local FEML-Discretized 2D anisotropic Poisson equation
The diffusive elemental matrix in FEM (frequently called “stiffness matrix”) on an element is given by
|
|
where is the matrix representing the anisotropic diffusion tensor, and the matrix is given explicitly by
|
|
Since the matrix is constant on an element of the mesh, the integral is easy to compute. Thus, the difussive matrix for a linear triangular element (FEML) is given by
|
|
Now, let us consider the first diagonal entry of the local FEML anisotropic Poisson diffusive matrix ,
|
|
where is the anticlockwise rotation,
|
|
In this notation, the diffusive term in local FEML is given as follows
|
|
5.3 Comparison between local DEC and FEML discretizations
For the sake of brevity, we are only going to compare the entries of the first row and first column of each formulation. Consider the various lengths, areas and angles labeled in Figures 6 and 7.
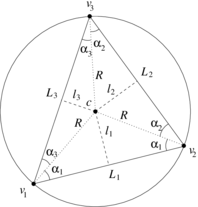
|
| Figure 7. Circumscribed triangle. |
We have the following identities:
|
|
5.3.1 The diffusive term
For instance, we claim that
|
|
Indeed,
|
|
Thus,
|
|
All we have to do now is show that
|
|
Note that, since is orthogonal to , must be parallel to . Thus,
|
|
(14) |
Now we are going to express in terms of . Let us consider
|
|
where are coefficients to be determined. Taking inner products with and we get the two equations
|
|
Solving for and
|
|
Substituting all the relevant quantities in (14) we have, for instance, that the coefficient of is
|
|
and similarly for the coefficient of . The calculations for the remaining entries are similar.
Thus, the local DEC and FEML diffusive terms of the 2D anisotropic Poisson equation coincide.
5.3.2 The source term
As already observed in [6], the right hand sides of the local DEC and FEML systems are different
|
|
While FEML uses a barycentric subdivision to calculate the areas associated to each node/vertex, DEC uses a circumcentric subdivision. Eventually, this leads the DEC discretization to a better approximation of the solution (on coarse meshes).
6. Some remarks about DEC quantities
6.1 The discrete Hodge star quantities revisited
The numbers appearing in the local DEC matrices can be expressed both in terms of determinants and in terms of trigonometric functions. More precisely,
|
|
These expressions are valid regardless of the location of the circumcenter and can, indeed, take negative values. The angles that are measured in the scheme can be negative as in the obtuse triangle of Figure 8.
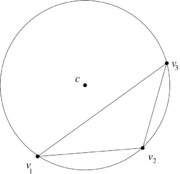
|
|
| Figure 8. Negative (exterior) angles measured in an obtuse triangle. |
and some quantities can even be zero. For instance, if
|
|
then
|
|
6.2 Area weights assigned to vertices
In order to understand how local DEC assigns area weights to vertices differently from FEML, let us consider the obtuse triangle shown in Figure 8. Let be the middle points of the segments respectively. As shown in Figure 9, the triangle lies completely outside of the triangle . Geometrically, this implies that its area must be assigned a negative sign, which is confirmed by the determinant formulas of Subsection 6.1. On the other hand, the triangle will have positive area. Thus, their sum gives us the area in Figure 9.
|
|
|
| Figure 9: Area weight assigned to |
The area is computed similarly, where the triangle is assigned negative area (see Figure 10).
|
|
|
| Figure 10: Area weight assigned to |
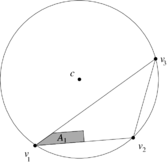
Note that for , the two triangles and both have positive areas (Figure 11).
|
|
|
| Figure 11: Area weight assigned to |
7 Numerical Examples
In this section, we present three numerical examples in order to illustrate the performance of DEC resulting from the local formulation and its implementation. In all cases, we solve the anisotropic Poisson equation. The FEML methodology that we have used in the comparison can be consulted [11,13,2].
7.1 First example: Heterogeneity
This example is intended to highlight how Local DEC deals effectively with heterogeneous materials. Consider the region in the plane given in Figure 12.
|
| Figure 12: Square and inner circle with different conditions. |
- The difussion constant for the region labelled mat1 is and its source term is .
- The difussion constant for the region labelled mat2 is and its source term is .
|
|
|
| (13) | (13) | (c) |
| Figure 13 | ||

|

|

|
| (a) | (b) | (c) |
| Figure 14: Six of the meshes used in the first example. | ||
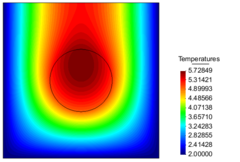
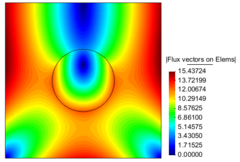
The numerical results for the maximum temperature value are exemplified in Table 7.1.
| Mesh | nodes | elements | Max. Temp. Value | Max. Flux Magnitude | ||
| DEC | FEML | DEC | FEML | |||
| Figure 14(a) | 49 | 80 | 5.51836 | 5.53345 | 13.837 | 13.453 |
| Figure 14(b) | 98 | 162 | 5.65826 | 5.66648 | 14.137 | 14.024 |
| Figure 14(c) | 258 | 466 | 5.70585 | 5.71709 | 14.858 | 14.770 |
| Figure 14(d) | 1,010 | 1,914 | 5.72103 | 5.72280 | 15.008 | 15.006 |
| Figure 14(e) | 3,813 | 7,424 | 5.72725 | 5.72725 | 15.229 | 15.228 |
| Figure 14(f) | 13,911 | 27,420 | 5.72821 | 5.72826 | 15.342 | 15.337 |
| 50,950 | 101,098 | 5.72841 | 5.72842 | 15.395 | 15.396 | |
| 135,519 | 269,700 | 5.72845 | 5.72845 | 15.420 | 15.417 | |
| 298,299 | 594,596 | 5.72848 | 5.72848 | 15.430 | 15.429 | |
| 600,594 | 1,198,330 | 5.72848 | 5.72848 | 15.433 | 15.433 | |
| 1,175,238 | 2,346,474 | 5.72849 | 5.72849 | 15.43724 | 15.43724 | |
|
|
| (a) Contour Fill of Temperatures | (b) Contour Fill of Flux vectors on Elems |
| Figure 15: Temperature and flux-magnitude distribution fields of the first example. | |

|

|
| (a) | (b) |

|

|
| (c) | (d) |

|

|
| (e) | (f) |
| Figure 16: Temperature and Flux magnitude graphs of the first example along a cross-section of the domain for different meshes. | |
In Table 1, we show some global error metrics for different meshes. Figure 17 shows the error evolution in norm for this example.
| Mesh | Nodes | norm | |
| 1 | 49 | 1.0537e-02 | 1.4438e-01 |
| 2 | 98 | 4.2447e-03 | 4.8558e-02 |
| 3 | 258 | 6.9781e-04 | 3.0390e-03 |
| 4 | 1,010 | 8.8386e-05 | 1.4877e-04 |
| 5 | 3,813 | 1.0736e-05 | 7.7369e-06 |
| 6 | 13,911 | 1.4422e-06 | 4.9791e-07 |
| 7 | 50,950 | 1.7582e-07 | 2.9608e-08 |
| 8 | 135,518 | 3.2621e-08 | 2.9233e-09 |
| 9 | 298,299 | 7.3566e-09 | 3.3610e-10 |
| 10 | 603,440 | 1.8577e-09 | 4.9496e-11 |

|
| Figure 17: DEC |
7.2 Second example: Anisotropy
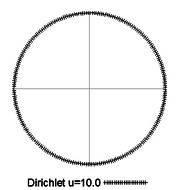
Let us solve the Poisson equation in a circle of radius one centered at the origin under the following conditions (see Figure 18):
- heat anisotropic diffusion constants ;
- material angle ;
- source term ;
- Dirichlet boundary condition .
|
| Figure 18: Disk of radius one. |
|
|
|
|
| (a) | (b) | (c) | (d) |

|

| ||
| (e) | (f) | ||
| Figure 19: First six meshes used for unit disk. | |||
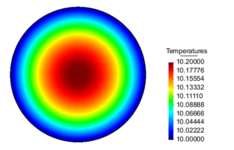
The numerical results for the maximum temperature value () are exemplified in Table 7.2 where a comparison with the Finite Element Method with linear interpolation functions (FEML) is also shown.
| Mesh | nodes | elements | Temp. Value at | Flux Magnitude at | ||
| DEC | FEML | DEC | FEML | |||
| Figure 19(a) | 17 | 20 | 10.20014 | 10.19002 | 0.42133 | 0.43865 |
| Figure 19(b) | 41 | 56 | 10.20007 | 10.19678 | 0.48544 | 0.49387 |
| Figure 19(c) | 201 | 344 | 10.20012 | 10.20158 | 0.52470 | 0.52428 |
| Figure 19(d) | 713 | 1304 | 10.20000 | 10.19969 | 0.54143 | 0.54224 |
| Figure 19(e) | 2455 | 4660 | 10.20000 | 10.19990 | 0.54971 | 0.55138 |
| Figure 19(f) | 8180 | 15862 | 10.20000 | 10.20002 | 0.55326 | 0.55409 |
| 20016 | 39198 | 10.20000 | 10.19999 | 0.55470 | 0.55520 | |
| 42306 | 83362 | 10.20000 | 10.20000 | 0.55540 | 0.55572 | |
|
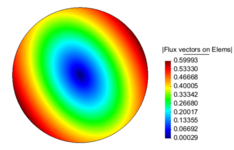
|
| (a) Contour Fill of Temperatures | (b) Contour Fill of Flux vectors on Elems |
| Figure 20: Temperature distribution and Flux magnitude fields for the finest mesh of the second example. | |

|

|
| (a) | (b) |

|

|
| (c) | (d) |

|

|
| (e) | (f) |
| Figure 21: Temperature and Flux magnitude graphs of the second example along a diameter of the circle for different meshes: mesh in Figure | |
In Table 2, we show some global error metrics for different meshes. Figure 22 shows the error evolution in norm for this example.
| Mesh | Nodes | norm | |
| 1 | 17 | 1.5818e-04 | 2.3555e-06 |
| 2 | 51 | 2.5395e-05 | 1.5639e-07 |
| 3 | 201 | 3.3643e-06 | 1.0517e-08 |
| 4 | 713 | 5.1563e-07 | 8.3543e-10 |
| 5 | 2,455 | 8.9235e-08 | 7.6073e-11 |
| 6 | 8,180 | 3.1731e-08 | 2.9858e-11 |
| 7 | 20,016 | 2.0217e-08 | 2.6580e-11 |
| 8 | 42,306 | 1.4421e-08 | 2.7062e-11 |
| 9 | 82,722 | 9.8533e-09 | 2.6164e-11 |
| 10 | 156,274 | 7.1352e-09 | 2.5954e-11 |
| 11 | 420,013 | 4.4277e-09 | 2.6151e-11 |
| 12 | 935,016 | 2.9635e-09 | 2.6003e-11 |

|
| Figure 22: DEC |
7.3 Third example: Heterogeneity and anisotropy
Let us solve the Poisson equation in a circle of radius on the following domain (see Figure 23) with various material properties. The geometry of the domain is defined by segments of ellipses passing through the given points which have centers at the origin .
|
| Figure 23: Egg-like domain with different materials. |
| Point | Point | ||||
| a | -5 | 0 | A | 0 | -4 |
| b | -4 | 0 | B | 0 | -3 |
| c | -3 | 0 | C | 0 | -2 |
| d | -1 | 0 | D | 0 | -1 |
| e | 1 | 0 | E | 0 | 1 |
| f | 6 | 0 | F | 0 | 2 |
| g | 7 | 0 | G | 0 | 3 |
| h | 8 | 0 | H | 0 | 4 |
- The Dirichlet boundary condition is and material properties (anisotropic heat diffusion constants, material angles and source terms) are given according to Figure 24 and the table below.

|
| Figure 24: Dirichlet condition. |
| angle | ||||
| Domain mat1 | 5 | 25 | 30 | 15 |
| Domain mat2 | 25 | 5 | 0 | 5 |
| Domain mat3 | 50 | 12 | 45 | 5 |
| Domain mat4 | 10 | 35 | 0 | 5 |
|
|

|
| (a) | (b) | (c) |
| ||
| (d) | ||
| Figure 25: Meshes for layered egg-like figure. | ||
The numerical results for the maximum temperature value () are exemplified in Table 7.3 where a comparison with the Finite Element Method with linear interpolation functions (FEML) is also shown.
| Mesh | nodes | elements | Max. Temp. Value | Max. Flux Magnitude | ||
| DEC | FEML | DEC | FEML | |||
| Figure 25(a) | 342 | 616 | 2.79221 | 2.79854 | 18.41066 | 18.40573 |
| Figure 25(b) | 1,259 | 2,384 | 2.83929 | 2.84727 | 18.93838 | 18.91532 |
| Figure 25(c) | 4,467 | 8,668 | 2.85608 | 2.85717 | 19.13297 | 19.13193 |
| Figure 25(d) | 14,250 | 28,506 | 2.85994 | 2.86056 | 19.20982 | 19.20909 |
| 20,493 | 40,316 | 2.86120 | 2.86177 | 19.23120 | 19.23457 | |
| 60,380 | 119,418 | 2.86219 | 2.86231 | 19.26655 | 19.26628 | |
| 142,702 | 283,162 | 2.86249 | 2.86256 | 19.28045 | 19.28028 | |
| 291,363 | 579,360 | 2.86263 | 2.86267 | 19.28727 | 19.28755 | |
| 495,607 | 986,724 | 2.86275 | 2.86269 | 19.29057 | 19.29081 | |
| 1,064,447 | 2,122,160 | 2.86272 | 2.86273 | 19.29385 | 19.29389 | |
| 2,106,077 | 4,202,536 | 2.86274 | 2.86274 | 19.29618 | 19.29615 | |
| 4,031,557 | 8,049,644 | 2.86275 | 2.86275 | 19.29763 | 19.29765 | |

|

|
| (a) Contour Fill of Temperatures | (b) Contour Fill of Flux vectors on Elems |
| Figure 26: Temperature distribution and Flux magnitude fields for the finest mesh of the third example. | |

|

|
| (a) | (b) |

|

|
| (c) | (d) |

|

|
| (e) | (f) |
| Figure 27: Temperature and Flux magnitude graphs of the third example along a cross-section of the domain for different meshes: Mesh in Figure | |
In Table 3, we show some global error metrics for different meshes. Figure 28 shows the error evolution in norm for this example.
| Mesh | Nodes | norm | |
| 1 | 342 | 9.3638e-04 | 2.7786e-02 |
| 2 | 1,259 | 1.5173e-04 | 3.2731e-03 |
| 3 | 4,467 | 2.2110e-05 | 2.2937e-04 |
| 4 | 14,250 | 3.7233e-06 | 1.9151e-05 |
| 5 | 20,492 | 2.2311e-06 | 9.5930e-06 |
| 6 | 60,380 | 4.3769e-07 | 8.7330e-07 |
| 7 | 142,702 | 1.1664e-07 | 1.3926e-07 |
| 8 | 291,369 | 3.9764e-08 | 3.3314e-08 |
| 9 | 497,378 | 1.6680e-08 | 1.0275e-08 |
| 10 | 1,067,171 | 3.9594e-09 | 1.2190e-09 |
| 11 | 2,106,248 | 9.6949e-10 | 1.4415e-10 |

|
| Figure 28: DEC |
Remark. As can be seen from the previous examples, DEC behaves well on coarse meshes. As expected, the results of DEC and FEML are identical for fine meshes. We would also like to point out the the computational costs of DEC and FEML are very similar since the local matrices are very similar in profile, or even identical in some cases.
8. Conclusions
DEC is a relatively recent discretization scheme for PDE's which takes into account the geometric and analytic features of the operators and the domains involved. The main contributions of this paper are the following:
- We have made explicit the local formulation of DEC, i.e. on each triangle of the mesh. As is customary, the local pieces can be assembled, which facilitates the implementation of DEC by the interested reader. Furthermore, the profiles of the assembled DEC matrices are equal to those of assembled FEML matrices.
- Guided by the local formulation, we have deduced a natural way to approximate the flux/gradient vector of a discretized function, which coincides with that of FEML. Such approximate flux vector automatically gives the discretized version of the anisotropic flux.
- We have discretized the pullback operator on continuous 1-forms using Whitney interpolation forms and have found the discrete anisotropy operator for primal 1-forms.
- We have deduced the local DEC formulation of the 2D anisotropic Poisson equation, and have proved that the DEC and FEML diffusion terms are identical, while the source terms are not – due to the different area-weight allocation for the nodes.
- Local DEC allows a simple treatment of heterogeneous material properties assigned to subdomains (element by element), which eliminates the need of dealing with it through ad hoc modifications of the global discrete Hodge star operator matrix.
On the other hand we would like to point the following features:
- The area weights assigned to the nodes of the mesh when solving the 2D anisotropic Poisson equation can even be negative (when a triangle has an inner angle greater that ), in stark contrast to the FEML formulation.
- The computational cost of DEC is similar to that of FEML. While the numerical results of DEC and FEML on fine meshes are virtually identical, the DEC solutions are better than those of FEML on coarse meshes. Furthermore, DEC solutions display numerical convergence, as shown by the error measurements.
Our future work will include the DEC discretization of convective terms, and DEC on 2-dimensional simplicial surfaces in 3D. Preliminary results on both problems are promising and competitive with FEML.
Acknowledgements
The second named author was partially supported by a CONACyT grant, and would like to thank the International Centre for Numerical Methods in Engineering (CIMNE) and the University of Swansea for their hospitality. We gratefully acknowledge the support of NVIDIA Corporation with the donation of the Titan X Pascal GPU used for this research.
References
[1] Bossavit, A.: “Mixed finite elements and the complex of Whitney forms.” In J. Whiteman, editor, The mathematics of finite elements and applications VI, pages 137–144. Academic Press, 1988. [2] Botello, S.; Moreles, M.Z.; Oñate, E.: ``Módulo de Aplicaciones del Método de los Elementos Finitos para resolver la ecuación de Poisson: MEFIPOISS. Aula CIMNE-CIMAT, Septiembre 2010, ISBN 978-84-96736-95-5. [3] Cartan, E.: ``Sur certaines expressions différentielles et le probleme de Pfaff". Annales Scientifiques de l'École Normale Supérieure. Série 3. Paris: Gauthier-Villars. 16: 239?332 (1899) [4] Crane, Keenan, et al. “Digital geometry processing with discrete exterior calculus.” ACM SIGGRAPH 2013 Courses. ACM, 2013. [5] Dassios, Ioannis, et al. “A mathematical model for plasticity and damage: A discrete calculus formulation.” Journal of Computational and Applied Mathematics 312 (2017): 27-38. [6] Esqueda, H.; Herrera, R.; Botello, S; Moreles, M. A.: “A geometric description of Discrete Exterior Calculus for general triangulations”. Rev. int. métodos numér. cálc. diseño ing. (Online first). https://www.scipedia.com/public/Herrera_et_al_2018b [7] Griebel, Michael, Christian Rieger, and Alexander Schier. “Upwind Schemes for Scalar Advection-Dominated Problems in the Discrete Exterior Calculus.” Transport Processes at Fluidic Interfaces. Birkhäuser, Cham, 2017. 145-175. [8] Hirani, Anil Nirmal. “Discrete exterior calculus”. Diss. California Institute of Technology, 2003. [9] Hirani, Anil N., Kalyana B. Nakshatrala, and Jehanzeb H. Chaudhry. “Numerical method for Darcy flow derived using Discrete Exterior Calculus.” International Journal for Computational Methods in Engineering Science and Mechanics 16.3 (2015): 151-169. [10] Mohamed, Mamdouh S., Anil N. Hirani, and Ravi Samtaney. “Discrete exterior calculus discretization of incompressible Navier-Stokes equations over surface simplicial meshes.” Journal of Computational Physics 312 (2016): 175-191. [11] Oñate, E.: “4 - 2D Solids. Linear Triangular and Rectangular Elements,” in Structural Analysis with the Finite Element Method. Linear Statics, Volume 1: Basis and Solids, CIMNE-Springer, Barcelona, 2009. Pages 117-157, ISBN 978-1-4020-8733-2 [12] Whitney, H.: “Geometric Integration Theory.” Princeton University Press, 1957.[13] O. C. Zienkiewicz, R. L. Taylor and J. Z. Zhu: “3 - Generalization of the finite element concepts. Galerkin-weighted residual and variational approaches,” In The Finite Element Method Set (Sixth Edition), Butterworth-Heinemann, Oxford, 2005, Pages 54-102, ISBN 9780750664318,
Document information
Published on 19/06/20
Accepted on 24/05/20
Submitted on 22/04/20
Volume 36, Issue 2, 2020
DOI: 10.23967/j.rimni.2020.05.003
Licence: CC BY-NC-SA license