m (Cinmemj moved page Draft Samper 411837410 to Bonilla et al 2019a) |
|||
| (76 intermediate revisions by the same user not shown) | |||
| Line 140: | Line 140: | ||
No obstante, la extrapolación directa de estos parámetros hemodinámicos es complicada, pues la circulación de la sangre está dentro del cuerpo vivo, por lo que debe haber un compromiso entre la precisión de las mediciones y su nivel de invasividad al determinarlas [30]. | No obstante, la extrapolación directa de estos parámetros hemodinámicos es complicada, pues la circulación de la sangre está dentro del cuerpo vivo, por lo que debe haber un compromiso entre la precisión de las mediciones y su nivel de invasividad al determinarlas [30]. | ||
| − | La necesidad de seguir investigando acerca de estos sistemas debido a la trascendencia e impacto en la salud mundial que tienen, hace que se realicen estudios y descubrimientos de manera continuada con el fin de mejorar los tratamientos ya existentes, descubrir factores de relevancia y prevenir el efecto de diferentes hábitos o costumbres en la fisiología de este sistema tan importante. Es en este marco donde se sitúa este trabajo, en servir de utilidad recreando mediante una simulación numérica el flujo sanguíneo en una situación característica, pero aplicable a otras circunstancias [16 | + | La necesidad de seguir investigando acerca de estos sistemas debido a la trascendencia e impacto en la salud mundial que tienen, hace que se realicen estudios y descubrimientos de manera continuada con el fin de mejorar los tratamientos ya existentes, descubrir factores de relevancia y prevenir el efecto de diferentes hábitos o costumbres en la fisiología de este sistema tan importante. Es en este marco donde se sitúa este trabajo, en servir de utilidad recreando mediante una simulación numérica el flujo sanguíneo en una situación característica, pero aplicable a otras circunstancias [16,22,23]. |
Este hecho permite una interpretación sencilla y rápida, mediante la analogía a un sistema eléctrico menos complejo –al tratarse de un sistema de orden reducido-, de lo que está sucediendo y anticipándose al comportamiento de una red arterial en concreto en una situación específica. | Este hecho permite una interpretación sencilla y rápida, mediante la analogía a un sistema eléctrico menos complejo –al tratarse de un sistema de orden reducido-, de lo que está sucediendo y anticipándose al comportamiento de una red arterial en concreto en una situación específica. | ||
| Line 163: | Line 163: | ||
'''''Pinceladas históricas''''' | '''''Pinceladas históricas''''' | ||
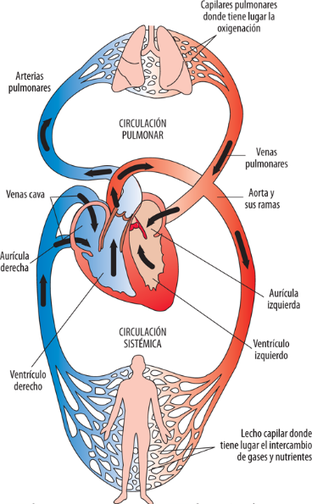
| − | Partiendo del siglo IV a.C. ''Aristóteles'' describió la comunicación del corazón con los vasos sanguíneos, aunque no identificó todavía la circulación la circulación sanguínea. Siguiendo al siglo III a.C. ''Praxágoras'', distinguió las funciones de las arterias y las venas, observando que las arterias impulsaban sangre y las venas no [28 | + | Partiendo del siglo IV a.C. ''Aristóteles'' describió la comunicación del corazón con los vasos sanguíneos, aunque no identificó todavía la circulación la circulación sanguínea. Siguiendo al siglo III a.C. ''Praxágoras'', distinguió las funciones de las arterias y las venas, observando que las arterias impulsaban sangre y las venas no [28,29]. A finales del siglo II, el griego ''Galeno'' propuso que se propagaban los pulsos de presión originados en el corazón a través de la red arterial [24]. |
Durante un período más avanzado, alrededor del siglo XIII, ''Ibn Al-Nafi'' fue el primer médico que describió correctamente la circulación pulmonar [24]. Antes de eso, la teoría común y popular del flujo sanguíneo era que la comida se convertía en sangre en el hígado y luego funcionaba como un combustible. | Durante un período más avanzado, alrededor del siglo XIII, ''Ibn Al-Nafi'' fue el primer médico que describió correctamente la circulación pulmonar [24]. Antes de eso, la teoría común y popular del flujo sanguíneo era que la comida se convertía en sangre en el hígado y luego funcionaba como un combustible. | ||
| Line 414: | Line 414: | ||
El plasma a su vez, es una solución electrolítica diluida que contiene varias proteínas y diferentes sustancias disueltas. También transporta nutrientes, azucares, hormonas y substancias de desecho contenidos en la sangre. Al contener una gran cantidad de agua, y al ser ésta incomprensible, da las propiedades de incompresibilidad a la sangre. | El plasma a su vez, es una solución electrolítica diluida que contiene varias proteínas y diferentes sustancias disueltas. También transporta nutrientes, azucares, hormonas y substancias de desecho contenidos en la sangre. Al contener una gran cantidad de agua, y al ser ésta incomprensible, da las propiedades de incompresibilidad a la sangre. | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 65%;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[Image:Draft_Samper_411837410-image8.png|center|396px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
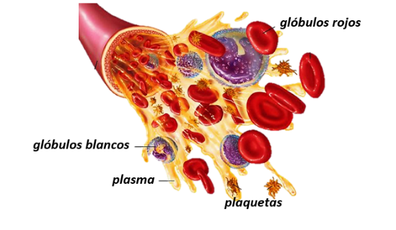
| + | | colspan="1" style="padding:10px;" | '''Figura 7'''. Composición de la sangre<br /> | ||
| + | Fuente:https://www.google.es/search?q=composicion+de+la+sangre&source=lnms&tbm=isch&sa=X&ved=0ahUKEwi8_7_ViePdAhWSK1AKHeXCC98Q_AUICigB&biw=1280&bih=617&dpr=1.5 | ||
| + | |} | ||
| − | |||
| − | |||
| − | + | Desde un punto de vista mecánico, la sangre está compuesta por glóbulos rojos flexibles suspendidos en el plasma, que hacen que se comporte como un fluido no newtoniano debido a la heterogeneidad de su composición. Por tanto, cualquier modelo constitutivo que se proponga ha de reflejar como mínimo estas dos características, viscosidad e incomprensibilidad. No obstante, para el desarrollo de este trabajo, se toma la sangre como fluido newtoniano con una viscosidad propuesta de valor constante. | |
| − | + | ||
| − | + | ||
| − | + | ||
====2.4.4. Ondas de presión y flujo==== | ====2.4.4. Ondas de presión y flujo==== | ||
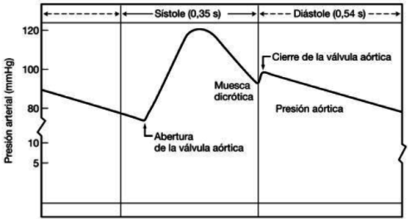
| Line 433: | Line 435: | ||
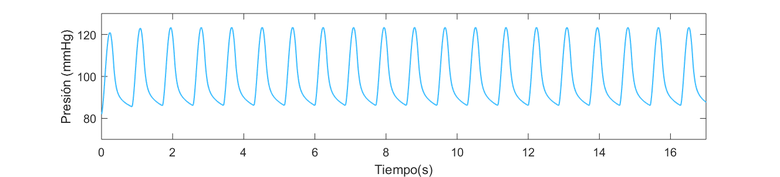
La diferencia entre la presión arterial sistólica y la diastólica se denomina presión diferencial o presión de pulso. | La diferencia entre la presión arterial sistólica y la diastólica se denomina presión diferencial o presión de pulso. | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[Image:Draft_Samper_411837410-image9-c.png|center|408px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
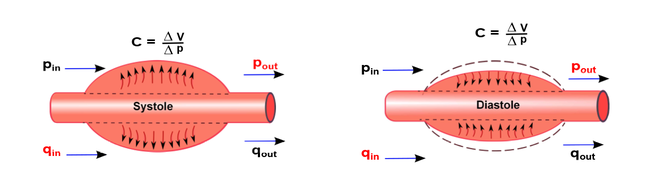
| + | | colspan="1" style="padding-bottom:10px;" | '''Figura 8'''. Curva de presión durante la sístole y la diástole<br /> | ||
| + | Fuente: https://ocw.unican.es/mod/page/view.php?id=538 | ||
| + | |} | ||
| − | |||
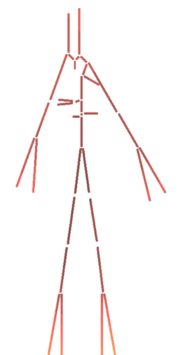
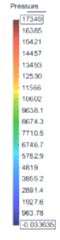
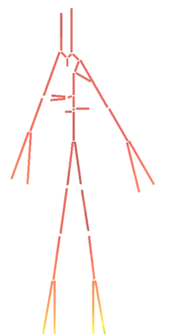
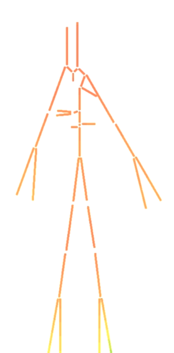
| + | Las formas de la onda de presión y su velocidad dependen tanto del rendimiento del corazón como de las características de la red vascular. La Figura 9 muestra cómo la presión disminuye a medida que se aumenta la distancia respecto al corazón. | ||
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | |
| − | + | |- | |
| − | + | | style="padding:10px;" | [[Image:Draft_Samper_411837410-image10.png|414px]] | |
| − | + | |- style="text-align: center; font-size: 75%;" | |
| − | + | | colspan="1" style="padding-bottom:10px;" | '''Figura 9'''. Presión pulsátil en el árbol vascular<br /> | |
| − | + | Fuente: D.Corridini. A numerical tool for the simulation of the blood flow, 2014 | |
| − | + | |} | |
| − | + | ||
| − | + | ||
| − | |||
| − | |||
Durante el período de diástole, la presión en el ventrículo izquierdo es cercana a cero y la válvula aórtica se mantiene cerrada a causa de la diferencia de presión de aproximadamente unos 80 mmHg. En la aorta, la presión arterial media es aproximadamente de unos 100 mmHg con una presión sistólica de 120 mmHg y una presión diastólica de 80 mmHg. En las arteriolas la presión disminuye considerablemente y tanto la presión diastólica como la sistólica convergen gradualmente. Cuando llega el flujo sanguíneo al sistema de capilares, el flujo es aproximadamente constante y más lento, lo que facilidad el intercambio mediante difusión, de nutrientes y productos de desecho entre la sangre y el tejido enervado. | Durante el período de diástole, la presión en el ventrículo izquierdo es cercana a cero y la válvula aórtica se mantiene cerrada a causa de la diferencia de presión de aproximadamente unos 80 mmHg. En la aorta, la presión arterial media es aproximadamente de unos 100 mmHg con una presión sistólica de 120 mmHg y una presión diastólica de 80 mmHg. En las arteriolas la presión disminuye considerablemente y tanto la presión diastólica como la sistólica convergen gradualmente. Cuando llega el flujo sanguíneo al sistema de capilares, el flujo es aproximadamente constante y más lento, lo que facilidad el intercambio mediante difusión, de nutrientes y productos de desecho entre la sangre y el tejido enervado. | ||
''Observación: Para un adulto joven y sano los valores aceptables de presión sistólica y diastólica oscilan entre 120 mmHg y 80 mmHg respectivamente. No obstante, factores constitucionales (sexo, raza, peso) y del estilo de vida (dieta, hábitos como el consumo de tabaco o alcohol, etc.) influyen de forma muy importante en la presión arterial haciendo variar los valores y la forma de la onda. '' | ''Observación: Para un adulto joven y sano los valores aceptables de presión sistólica y diastólica oscilan entre 120 mmHg y 80 mmHg respectivamente. No obstante, factores constitucionales (sexo, raza, peso) y del estilo de vida (dieta, hábitos como el consumo de tabaco o alcohol, etc.) influyen de forma muy importante en la presión arterial haciendo variar los valores y la forma de la onda. '' | ||
| − | |||
| − | |||
==3. Modelo matemático== | ==3. Modelo matemático== | ||
| − | En el capítulo anterior se proporcionó un conocimiento básico preliminar sobre el sistema cardiovascular. A lo largo de este capítulo veremos los modelos y las ecuaciones matemáticas utilizadas que describen el flujo y la presión sanguínea mediante un modelo elástico lineal y otro visco elástico | + | En el capítulo anterior se proporcionó un conocimiento básico preliminar sobre el sistema cardiovascular. A lo largo de este capítulo veremos los modelos y las ecuaciones matemáticas utilizadas que describen el flujo y la presión sanguínea mediante un modelo elástico lineal y otro visco elástico [12]. Los modelos matemáticos permiten, no solo estudiar la propagación de las ondas en un segmento arterial aislado, sino también el sistema de circulación global, o al menos, aproximar su comportamiento. |
| − | + | ||
| − | + | ||
===3.1. Modelos de orden reducido 0-D=== | ===3.1. Modelos de orden reducido 0-D=== | ||
| Line 469: | Line 470: | ||
Estos modelos describen la física del sistema muy simple y el cambio de parámetros da una idea del comportamiento del sistema implementado. Se pueden encontrar diferentes modelos según los parámetros utilizados y si trabajan en un solo bloque –modelo ''unicompartimentado''- o que se trabajan en varios bloques – modelo ''policompartimentado''-. | Estos modelos describen la física del sistema muy simple y el cambio de parámetros da una idea del comportamiento del sistema implementado. Se pueden encontrar diferentes modelos según los parámetros utilizados y si trabajan en un solo bloque –modelo ''unicompartimentado''- o que se trabajan en varios bloques – modelo ''policompartimentado''-. | ||
| − | |||
| − | |||
====3.1.1. Modelo unicompartimentado==== | ====3.1.1. Modelo unicompartimentado==== | ||
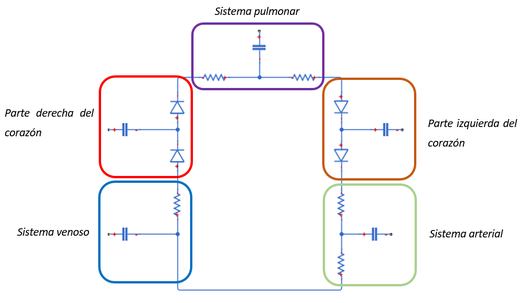
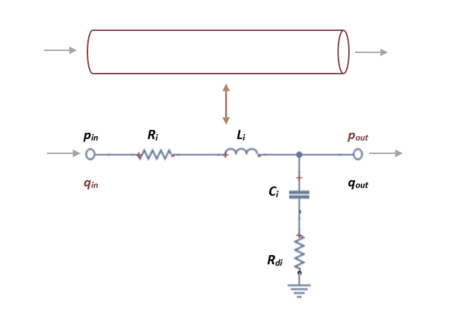
| − | En un modelo ''unicompartimentado'', la red arterial o venosa de todo el sistema se representa con un solo circuito, compuesto de una resistencia, una inductancia y/o un condensador. Este tipo de modelo se empezó a utilizar para modelar la circulación del cuerpo entero, –un bloque para la circulación arterial, otro bloque para la circulación pulmonar, etc.- pero estaba limitado puesto que no puede describir los cambios de presión y de caudal en ubicaciones específicas de la red arterial | + | En un modelo ''unicompartimentado'', la red arterial o venosa de todo el sistema se representa con un solo circuito, compuesto de una resistencia, una inductancia y/o un condensador. Este tipo de modelo se empezó a utilizar para modelar la circulación del cuerpo entero, –un bloque para la circulación arterial, otro bloque para la circulación pulmonar, etc.- pero estaba limitado puesto que no puede describir los cambios de presión y de caudal en ubicaciones específicas de la red arterial (Figura 10). |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 60%;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[Image:Draft_Samper_411837410-image11.png|center|522px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;" | '''Figura 10'''. Modelo esquemático tipo unicompartimentado simulando la circulación en cada sistema. Cada mini-modelo equivale a un sistema específico | ||
| + | |} | ||
| − | + | ====3.1.2. Modelo policompartimentado==== | |
| − | + | En los modelos ''policompartimentados'', por el contrario, la red arterial se divide en múltiples segmentos; cada arteria, como en el caso de este trabajo, está representada por un circuito eléctrico RLC (Figura 11). | |
| − | + | ||
| − | + | ||
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%;" | |
| − | + | |- | |
| − | ==== | + | | style="padding:10px;" | [[File:Draft_Samper_411837410_1323_Fig11.png|600px]] |
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Figura 11'''. Modelo esquemático tipo policompartimentado. Cada mini-modelo equivale a un vaso | ||
| + | |} | ||
| − | |||
Los valores de estos parámetros se calculan a partir de las propiedades de los vasos sanguíneos –módulo de Young, diámetro del vaso, longitud del vaso, grosor, viscosidad del fluido, entre otros. | Los valores de estos parámetros se calculan a partir de las propiedades de los vasos sanguíneos –módulo de Young, diámetro del vaso, longitud del vaso, grosor, viscosidad del fluido, entre otros. | ||
| − | |||
| − | |||
| − | |||
Con el fin de construir una red de vasos llenos, los circuitos eléctricos de cada segmento se conectan entre sí utilizando las condiciones adecuadas de salida y de bifurcación. Las condiciones de bifurcación se derivan de leyes de conservación de masa y del momento. Por eso, antes de construir la red, es fundamental conocer y considerar las características de cada segmento, es decir, su comportamiento mecánico, condiciones de bifurcación de flujo, etc. | Con el fin de construir una red de vasos llenos, los circuitos eléctricos de cada segmento se conectan entre sí utilizando las condiciones adecuadas de salida y de bifurcación. Las condiciones de bifurcación se derivan de leyes de conservación de masa y del momento. Por eso, antes de construir la red, es fundamental conocer y considerar las características de cada segmento, es decir, su comportamiento mecánico, condiciones de bifurcación de flujo, etc. | ||
Por lo tanto, los modelos que contienen parámetros agrupados en bloques poli-compartimentados, se consideran más adecuados para simular, estudiar y analizar el comportamiento general del sistema cardiovascular. Este tipo de modelo será el que se empleará en este trabajo. | Por lo tanto, los modelos que contienen parámetros agrupados en bloques poli-compartimentados, se consideran más adecuados para simular, estudiar y analizar el comportamiento general del sistema cardiovascular. Este tipo de modelo será el que se empleará en este trabajo. | ||
| − | |||
| − | |||
===3.2. Modelo matemático en 0-D=== | ===3.2. Modelo matemático en 0-D=== | ||
| Line 510: | Line 510: | ||
Dichos parámetros se pueden calcular usando ecuaciones matemáticas-sistema de ecuaciones diferenciales ordinarias acopladas que describen la variación en el tiempo- que dependen de las propiedades físicas y dimensiones de dichos vasos arteriales para la determinación de parámetros como presión y flujo. | Dichos parámetros se pueden calcular usando ecuaciones matemáticas-sistema de ecuaciones diferenciales ordinarias acopladas que describen la variación en el tiempo- que dependen de las propiedades físicas y dimensiones de dichos vasos arteriales para la determinación de parámetros como presión y flujo. | ||
| − | {| style=" | + | <div class="center" style="font-size: 75%;">'''Tabla 2'''. Analogía entre el sistema eléctrico y el sistema vascular |
| + | </div> | ||
| + | |||
| + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:55%;" | ||
|- | |- | ||
| − | | style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"|''SISTEMA VASCULAR'' | + | | style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"|'''SISTEMA VASCULAR''' |
| − | | style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"|''SISTEMA ELÉCTRICO'' | + | | style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"|'''SISTEMA ELÉCTRICO''' |
|- | |- | ||
| style="border: 1pt solid black;text-align: center;vertical-align: top;"|Presión'' (p) (mmHg)'' | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Presión'' (p) (mmHg)'' | ||
| Line 532: | Line 535: | ||
| − | + | En este apartado, se presenta la formulación matemática de los modelos con sus parámetros correspondientes, pues el trabajo se centrará en la representación de varios segmentos específicos del sistema arterial del cuerpo humano, diferenciándolos en su comportamiento visco elástico y elástico y comparándolos entre ellos (m<sup>3</sup>·Pa<sup>-1</sup>). | |
| − | + | ||
| − | + | ||
| − | En este apartado, se presenta la formulación matemática de los modelos con sus parámetros correspondientes, pues el trabajo se centrará en la representación de varios segmentos específicos del sistema arterial del cuerpo humano, diferenciándolos en su comportamiento visco elástico y elástico y comparándolos entre ellos | + | |
| − | + | ||
| − | + | ||
====3.2.1. Modelo equivalente 0-D al segmento vascular==== | ====3.2.1. Modelo equivalente 0-D al segmento vascular==== | ||
| − | |||
====3.2.1.1. Modelo elástico==== | ====3.2.1.1. Modelo elástico==== | ||
| − | Los modelos elásticos en estas mismas dimensiones se basan en la idea de que el flujo atraviesa un tubo cilíndrico rígido y recto de longitud establecida'' l'', espesor ''h ''y diámetro Ø. Teniendo en cuenta que los parámetros que lo componen simulan el comportamiento elástico de éste, su representación se adhiere a la | + | Los modelos elásticos en estas mismas dimensiones se basan en la idea de que el flujo atraviesa un tubo cilíndrico rígido y recto de longitud establecida'' l'', espesor ''h ''y diámetro Ø. Teniendo en cuenta que los parámetros que lo componen simulan el comportamiento elástico de éste, su representación se adhiere a la Figura 12. |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 50%;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_1015_Fig12.png|500px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Figura 12'''. Dimensiones y características de un vaso sanguíneo representado | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
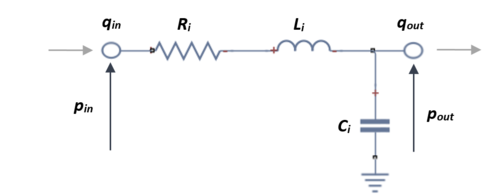
El circuito que modula un solo vaso arterial se ve representado por una resistencia, un condensador y una bobina, en el que se podrá calcular la presión que equivale al voltaje que lo atraviesa y el flujo, que equivale al amperaje. El modelo elástico se puede representar en un circuito L-invertido tal que así, | El circuito que modula un solo vaso arterial se ve representado por una resistencia, un condensador y una bobina, en el que se podrá calcular la presión que equivale al voltaje que lo atraviesa y el flujo, que equivale al amperaje. El modelo elástico se puede representar en un circuito L-invertido tal que así, | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[Image:Draft_Samper_411837410-image14-c.png|center|504px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Figura 13'''. Circuito equivalente (RLC) de un vaso. Qin y pin representa la corriente y el voltaje del fluido en la entrada del vaso respectivamente. Qout y pout es la corriente y el voltaje de salida del vaso | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Los parámetros a determinar en el circuito se describirán a continuación. | |
| − | ''3.2.1.1.1 Parámetros de flujo y presión'' | + | '''''3.2.1.1.1 Parámetros de flujo y presión'''''<br /> |
| − | :'' | + | :''a) Ecuaciones de presión y flujo en segmentos no terminales'' |
Como se ha precisado con anterioridad, mediante la analogía electrica se determinaran los parámetros fisiologicos de presión y flujo. Para ello, se definiran, dentro de cada segmento, dos únicas incognitas que, tras aplicar las leyes de corriente y voltage de ''Kirchhoff ''se obtendrá un sistema de dos ecuaciones diferenciales para presión <math display="inline">p</math>, y flujo <math display="inline">q</math>. | Como se ha precisado con anterioridad, mediante la analogía electrica se determinaran los parámetros fisiologicos de presión y flujo. Para ello, se definiran, dentro de cada segmento, dos únicas incognitas que, tras aplicar las leyes de corriente y voltage de ''Kirchhoff ''se obtendrá un sistema de dos ecuaciones diferenciales para presión <math display="inline">p</math>, y flujo <math display="inline">q</math>. | ||
| Line 570: | Line 571: | ||
De esto modo, serán las incógnitas en cada vaso a determinar, <math display="inline">\overset{\cdot}{{q}_{in}}</math> y <math display="inline">\overset{\cdot}{{p}_{out}}</math>, que se definirán como: | De esto modo, serán las incógnitas en cada vaso a determinar, <math display="inline">\overset{\cdot}{{q}_{in}}</math> y <math display="inline">\overset{\cdot}{{p}_{out}}</math>, que se definirán como: | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | | + | | |
| − | | | + | {| style="text-align: left; margin:auto;width: 100%;" |
|- | |- | ||
| − | | style="text-align: center;"|<math display="inline">\overset{\cdot}{{p}_{out}}=</math><math>\frac{{q}_{in}}{C}-\frac{{q}_{out}}{C}</math> como ecuación de presión | + | | style="text-align: center;"|<math display="inline">\overset{\cdot}{{q}_{in}}=</math><math>\frac{{p}_{in}}{L}-\frac{{p}_{out}}{L}-\frac{R{q}_{in}}{L}\qquad </math> como ecuación de flujo |
| − | | | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;"|<math display="inline">\overset{\cdot}{{p}_{out}}=</math><math>\frac{{q}_{in}}{C}-\frac{{q}_{out}}{C}\qquad </math> como ecuación de presión | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) | ||
|} | |} | ||
| Line 584: | Line 593: | ||
Por un lado, sabiendo que, la ecuación diferencial del cálculo del flujo en la arteria ''i'', donde <math display="inline">\overset{\cdot}{{q}_{i}}=</math><math>\, \frac{d{q}_{i}}{dt}</math>, se tiene que: | Por un lado, sabiendo que, la ecuación diferencial del cálculo del flujo en la arteria ''i'', donde <math display="inline">\overset{\cdot}{{q}_{i}}=</math><math>\, \frac{d{q}_{i}}{dt}</math>, se tiene que: | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-center: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| style="text-align: center;"|<math>\overset{\cdot}{{q}_{i}}=\frac{{p}_{(i-1)}-{p}_{i}-{R}_{i}{q}_{i}}{{L}_{i}}</math> | | style="text-align: center;"|<math>\overset{\cdot}{{q}_{i}}=\frac{{p}_{(i-1)}-{p}_{i}-{R}_{i}{q}_{i}}{{L}_{i}}</math> | ||
| − | | | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) | ||
|} | |} | ||
| + | siendo <math display="inline">{p}_{(i-1)}</math> la presión de salida del segmento anterior, <math display="inline">{p}_{i}</math> la presión'', '' <math display="inline">{R}_{i}</math>'' ''la resistencia, <math display="inline">{L}_{i}</math> la inductancia y <math display="inline">{q}_{i}</math> el flujo que se quiere determinar en un segmento indicado. | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 75%;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_5085_Fig14.png|600px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Figura 14'''. Analogía eléctrica entre dos vasos arteriales y el circuito eléctrico en segmentos no terminales | ||
| + | |} | ||
| − | |||
| − | |||
Por otro, la ecuación diferencial del cálculo de la presión en la arteria ''i'', donde <math display="inline">\overset{\cdot}{{p}_{i}}=</math><math>\, \frac{d{p}_{i}}{dt}</math>''' ''', se saca: | Por otro, la ecuación diferencial del cálculo de la presión en la arteria ''i'', donde <math display="inline">\overset{\cdot}{{p}_{i}}=</math><math>\, \frac{d{p}_{i}}{dt}</math>''' ''', se saca: | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-center: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| style="text-align: center;"|<math>\overset{\cdot}{{p}_{i}}=\frac{{q}_{i}-{q}_{(i+1)}}{{C}_{i}}</math> | | style="text-align: center;"|<math>\overset{\cdot}{{p}_{i}}=\frac{{q}_{i}-{q}_{(i+1)}}{{C}_{i}}</math> | ||
| − | | | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) | ||
|} | |} | ||
| + | siendo <math display="inline">{q}_{i}</math> el flujo calculado en el segmento indicado, <math display="inline">{q}_{(i+1)}</math> el flujo calculado en el segmento siguiente y <math display="inline">{C}_{i}</math> la complianza en ese segmento. | ||
| − | + | :''b) Ecuaciones de presión y flujo en segmentos terminales'' | |
| − | + | ||
| − | :'' | + | |
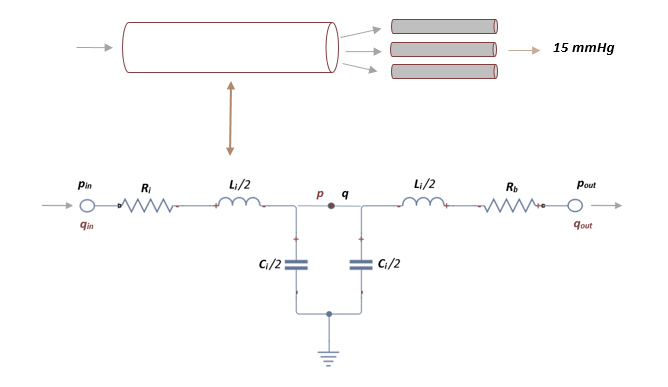
El segmento de red arterial que se utiliza en este trabajo se divide en un número finito de vasos que incluyen arteriolas y capilares. | El segmento de red arterial que se utiliza en este trabajo se divide en un número finito de vasos que incluyen arteriolas y capilares. | ||
| Line 614: | Line 635: | ||
Como en el caso anterior, aplicando las leyes de Kirchhoff, se obtiene un sistema de primer orden de 3 ecuaciones diferenciales'':'' | Como en el caso anterior, aplicando las leyes de Kirchhoff, se obtiene un sistema de primer orden de 3 ecuaciones diferenciales'':'' | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | | + | | |
| − | + | {| style="text-center: left; margin:auto;width: 100%;" | |
|- | |- | ||
| − | | style="text-align: center | + | | style="text-align: center;"|<math display="inline">\overset{\cdot}{{q}_{in}}=</math><math>\frac{{2p}_{in}}{L}-\frac{2p}{L}-\frac{2R{q}_{in}}{L}\qquad </math> como ecuación de flujo de entrada |
| − | | | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (7) | ||
|- | |- | ||
| − | | style="text-align: center; | + | | |
| − | | | + | {| style="text-center: left; margin:auto;width: 100%;" |
| + | |- | ||
| + | | style="text-align: center;"|<math display="inline">\overset{\cdot}{{q}_{out}}=</math><math>\frac{2p}{L}-\frac{{2p}_{out}}{L}-\frac{2{RbP}_{out}}{L}\qquad </math> como ecuación de flujo de salida | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (8) | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-center: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;"|<math display="inline">\overset{\cdot}{p}=</math><math>\frac{{q}_{in}}{C}-\frac{{q}_{out}}{C}\qquad </math> como ecuación de presión | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (9) | ||
|} | |} | ||
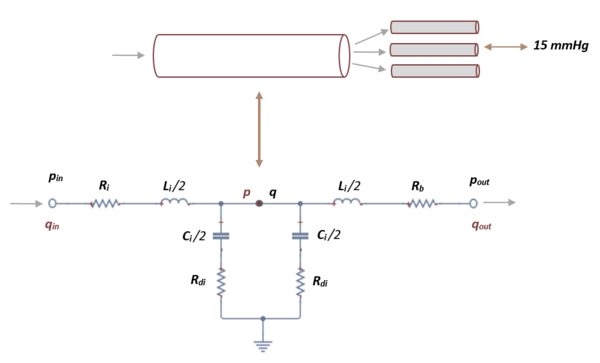
| + | donde <math display="inline">\overset{\cdot}{{q}_{in}}</math>, <math display="inline">\overset{\cdot}{{q}_{out}}</math>y <math display="inline">\overset{\cdot}{p\, }</math>son las variables a determinar. En cada segmento terminal, <math display="inline">{p}_{in\, }</math>es la presión obtenida en el segmento anterior y <math display="inline">{p}_{out}\,</math> mantiene un valor constante de 15 mmHg que representa la presión venosa media que se usa para calcular el flujo de salida en el límite, <math display="inline">{R}_{b}</math>es la resistencia terminal fija obtenida de la literatura [4]. | ||
| − | [[Image:Draft_Samper_411837410-image16-c.png|center| | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 65%;" |
| − | + | |- | |
| − | + | | style="padding:10px;" | [[Image:Draft_Samper_411837410-image16-c.png|center|700px]] | |
| − | + | |- style="text-align: center; font-size: 75%;" | |
| + | | colspan="1" style="padding:10px;" | '''Figura 15'''. Representación esquemática de la analogía eléctrica en un vaso terminal que fluye hacia capilares | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
====3.2.1.2. Modelo viscoelástico==== | ====3.2.1.2. Modelo viscoelástico==== | ||
| − | ''3.2.1.2.1 Parámetros de flujo y presión'' | + | '''''3.2.1.2.1 Parámetros de flujo y presión''''' |
| − | :'' | + | :''a) Ecuaciones de presión y flujo en segmentos no terminales'' |
El sistema visco elástico presenta las mismas características que la anterior en segmentos no terminales, es decir, las incógnitas son igualmente, <math display="inline">\overset{\cdot}{q}</math> y <math display="inline">\overset{\cdot}{p}</math> y se podrán obtener partiendo de las mismas características anatómicas de las arterias, como su longitud, diámetro, espesor, etc. Así pues, el flujo que atraviesa el vaso significativo se podrá calcular con: | El sistema visco elástico presenta las mismas características que la anterior en segmentos no terminales, es decir, las incógnitas son igualmente, <math display="inline">\overset{\cdot}{q}</math> y <math display="inline">\overset{\cdot}{p}</math> y se podrán obtener partiendo de las mismas características anatómicas de las arterias, como su longitud, diámetro, espesor, etc. Así pues, el flujo que atraviesa el vaso significativo se podrá calcular con: | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | <math>\overset{\cdot}{{q}_{i}}=\frac{{p}_{(i-1)}-{p}_{i}-{R}_{i}{q}_{i}}{{L}_{i}}</math> | + | | |
| − | | | + | {| style="text-align: left; margin:auto;width: 100%;" |
| + | |- | ||
| + | | style="text-align: center;" |<math>\overset{\cdot}{{q}_{i}}=\frac{{p}_{(i-1)}-{p}_{i}-{R}_{i}{q}_{i}}{{L}_{i}}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (10) | ||
|} | |} | ||
| − | + | siendo igualmente, <math display="inline">{p}_{(i-1)}</math> la presión de salida del segmento anterior, <math display="inline">{p}_{i}</math> la presión'', '' <math display="inline">{R}_{i}</math>'' ''la resistencia, <math display="inline">{L}_{i}</math> la inductancia y <math display="inline">{q}_{i}</math> el flujo requerido. | |
| − | + | ||
No obstante, antes de definir la ecuación de la presión, es importante conocer la mecánica del comportamiento del vaso, puesto que al contrario que antes, no es solamente elástico, sino que presenta un comportamiento visco elástico en su naturaleza dentro del S.C. Esta característica de la pared puede ser representada mediante el ''modelo de Voigt'' [12]. | No obstante, antes de definir la ecuación de la presión, es importante conocer la mecánica del comportamiento del vaso, puesto que al contrario que antes, no es solamente elástico, sino que presenta un comportamiento visco elástico en su naturaleza dentro del S.C. Esta característica de la pared puede ser representada mediante el ''modelo de Voigt'' [12]. | ||
| Line 659: | Line 695: | ||
Se define matemáticamente por una ecuación que relaciona el comportamiento elástico y viscoso del material: | Se define matemáticamente por una ecuación que relaciona el comportamiento elástico y viscoso del material: | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | | + | | |
| − | + | {| style="text-align: left; margin:auto;width: 100%;" | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | | + | | style="text-align: center;" | <math>\sigma =\underbrace{\quad \quad E\epsilon \quad \quad }_{\hbox{Componente elástico}} + \underbrace{\quad \quad\eta \frac{d\epsilon }{dt}\quad \quad}_{\hbox{Componente viscoso}}</math> |
| − | + | ||
|} | |} | ||
| − | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (11) | |
| − | | | + | |
|} | |} | ||
| + | donde <math display="inline">\sigma</math> es la tensión a la que está sometido el material, E es el módulo de Young, <math display="inline">\epsilon</math> la deformación que se le aplica, <math display="inline">\eta</math> la viscosidad del material, y <math display="inline">\frac{d\epsilon (t)}{dt}</math> es la derivada en función del tiempo de la tensión. | ||
| − | + | Con esto, la analogía eléctrica del modelo de Voigt se puede obtener considerando la resistencia '''R''' y la capacitancia '''C '''en serie [12]. Aplicando la ley de ''Kirchhoff'' sobre voltaje y corriente, se tiene: | |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | ||
| − | {| style="width: 100%; | + | |
|- | |- | ||
| − | | | + | | |
| − | + | {| style="text-align: left; margin:auto;width: 100%;" | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | | + | | style="text-align: center;" | <math>V= \underbrace{\quad \quad\frac{1}{C}Q\quad \quad}_{\hbox{Componente elástico}} |
| − | + | + \underbrace{\quad \quad R\frac{dQ}{dt}\quad \quad}_{\hbox{Componente viscoso}}</math> | |
|} | |} | ||
| − | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (12) | |
| − | | | + | |
|} | |} | ||
| + | donde <math display="inline">V</math> es voltaje, C la capacitancia, <math display="inline">Q\, \,</math> la carga, R la resistencia y <math display="inline">\frac{dQ}{dt}</math> la corriente eléctrica I. | ||
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 80%;" | |
| − | [[ | + | |- |
| − | + | | style="padding:10px;" | [[File:Draft_Samper_411837410_5603_Fig16.png|600px]] | |
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Figura 16'''. Representación esquemática mecánica y eléctrica equivalente del modelo de Voigt | ||
| + | |} | ||
En el caso de los vasos arteriales, la relación tensión-deformación o carga-voltaje se puede simplificar en términos de presión-volumen. La ecuación correspondiente explica la naturaleza visco elástica de la pared de los vasos siendo: | En el caso de los vasos arteriales, la relación tensión-deformación o carga-voltaje se puede simplificar en términos de presión-volumen. La ecuación correspondiente explica la naturaleza visco elástica de la pared de los vasos siendo: | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | | + | | |
| − | + | {| style="text-align: left; margin:auto;width: 100%;" | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | | + | | style="text-align: center;" | <math>p=\underbrace{\quad \quad\frac{1}{C}Q_c\quad \quad}_{\hbox{Componente elástico}} + \underbrace{\quad \quad R_{d}q\quad \quad}_{\hbox{Componente viscoso}}</math> |
| − | + | ||
|} | |} | ||
| − | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (13) | |
| − | | | + | |
|} | |} | ||
| + | donde <math display="inline">p</math> es la presión, <math display="inline">C</math> es la complianza del vaso, <math display="inline">{Q}_{c}</math> indica el volumen de sangre, <math display="inline">{R}_{d}</math> es la resistencia que mide viscosidad del vaso y <math display="inline">\frac{dQc}{dt}</math>= <math display="inline">{q}_{c}</math> es el flujo de sangre que atraviesa el vaso. Sabiendo que la incógnita <math display="inline">p</math> equivale a <math display="inline">p</math><sub>out</sub> , tomando la derivada de (ec.13) se obtiene, | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | <math>\overset{\cdot}{{p}_{out}}=\, \frac{{q}_{c}}{C}\, \, +{R}_{d}\overset{\cdot}{q}</math> | + | | |
| − | | | + | {| style="text-align: left; margin:auto;width: 100%;" |
| + | |- | ||
| + | | style="text-align: center;" |<math>\overset{\cdot}{{p}_{out}}=\, \frac{{q}_{c}}{C}\, \, +{R}_{d}\overset{\cdot}{q}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (14) | ||
|} | |} | ||
| + | donde se debe cumplir que, | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | ||
| − | {| style="width: 100%; | + | |
|- | |- | ||
| − | | | + | | |
| − | | | + | {| style="text-align: left; margin:auto;width: 100%;" |
|- | |- | ||
| − | | <math>\overset{\cdot}{{q}_{c}}={q}_{c}\, \overset{\cdot}{{q}_{in}}-0\quad</math> | + | | style="text-align: center;" | <math>{q}_{c}=\, {q}_{in}-{q}_{out}\quad</math> |
| − | | | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (15) | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" |<math>\overset{\cdot}{{q}_{c}}={q}_{c}\, \overset{\cdot}{{q}_{in}}-0\quad</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (16) | ||
|} | |} | ||
| + | y substituyendo en (ec.10), (ec.15) y (ec.16) en la (ec.14) para el cálculo de la presión en segmentos no terminales, finalmente obtenemos que, | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | ||
| − | {| style="width: 100%; | + | |
|- | |- | ||
| − | | <math>\overset{\cdot}{{p}_{out}}=\, \frac{{R}_{d}}{L}{p}_{in}+\, \left( \frac{1}{C}-\frac{{R}_{d}R}{L}\right) {q}_{in}-</math><math>\frac{{q}_{out}}{C}-\frac{{R}_{d}}{L}{p}_{out}</math> | + | | |
| − | | | + | {| style="text-align: left; margin:auto;width: 100%;" |
| + | |- | ||
| + | | style="text-align: center;" |<math>\overset{\cdot}{{p}_{out}}=\, \frac{{R}_{d}}{L}{p}_{in}+\, \left( \frac{1}{C}-\frac{{R}_{d}R}{L}\right) {q}_{in}-</math><math>\frac{{q}_{out}}{C}-\frac{{R}_{d}}{L}{p}_{out}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (17) | ||
|} | |} | ||
| + | que queda para la formula general, | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| − | {| style="width: 100%; | + | | |
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math>\overset{\cdot}{{p}_{i}}=\, \frac{{R}_{di}}{{L}_{i}}{p}_{(i-1)}+\, \left( \frac{1}{{C}_{i}}-\right. </math><math>\left. \frac{{R}_{di}{R}_{i}}{{L}_{i}}\right) {q}_{(i-1)}-\frac{{q}_{i}}{{C}_{i}}-</math><math>\frac{{R}_{di}}{{L}_{i}}{p}_{i}</math> | + | | style="text-align: center;" |<math>\overset{\cdot}{{p}_{i}}=\, \frac{{R}_{di}}{{L}_{i}}{p}_{(i-1)}+\, \left( \frac{1}{{C}_{i}}-\right. </math><math>\left. \frac{{R}_{di}{R}_{i}}{{L}_{i}}\right) {q}_{(i-1)}-\frac{{q}_{i}}{{C}_{i}}-</math><math>\frac{{R}_{di}}{{L}_{i}}{p}_{i}</math> |
| − | | | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (18) | ||
|} | |} | ||
| − | Hay que tener en cuenta que <math display="inline">{R}_{di}</math> es la resistencia que determina la viscosidad en particular que cada vaso específico, no es fija. Por lo tanto, cada segmento tendrá la suya propia, establecida por [12]. | + | Hay que tener en cuenta que <math display="inline">{R}_{di}</math> es la resistencia que determina la viscosidad en particular que cada vaso específico, no es fija. Por lo tanto, cada segmento tendrá la suya propia, establecida por [12]. |
| − | Así pues, la analogía eléctrica que representa el vaso no terminal y el sistema viscoelástico presenta la siguiente forma | + | Así pues, la analogía eléctrica que representa el vaso no terminal y el sistema viscoelástico presenta la siguiente forma (Figura 17). |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" |[[Image:Draft_Samper_411837410-image18.png|center|468px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Figura 17'''. Analogía eléctrica simplificada entre un vaso sanguíneo y su sistema viscoelástico | ||
| + | |} | ||
| − | |||
| − | : | + | :''b) Ecuaciones de presión y flujo en segmentos terminales'' |
| − | + | ||
| − | ''Ecuaciones de presión y flujo en segmentos terminales'' | + | |
En el caso visco elástico, en los segmentos terminales también se cierra la red arterial mediante una conexión en cascada de dos circuitos L y L invertidos. | En el caso visco elástico, en los segmentos terminales también se cierra la red arterial mediante una conexión en cascada de dos circuitos L y L invertidos. | ||
| Line 768: | Line 815: | ||
Aplicando pues, las leyes de Kirchhoff, se obtienen un total de 3 ecuaciones diferenciales de primer orden, | Aplicando pues, las leyes de Kirchhoff, se obtienen un total de 3 ecuaciones diferenciales de primer orden, | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | | + | | |
| − | + | {| style="text-align: left; margin:auto;width: 100%;" | |
|- | |- | ||
| − | | | + | | style="text-align: center;" |<math display="inline">\overset{\cdot}{{q}_{in}}=</math><math>\frac{{2p}_{(i-1)}}{{L}_{i}}-\frac{{2p}_{i}}{{L}_{i}}-\frac{2{R}_{i}{q}_{in}}{{L}_{i}}\qquad </math> como ecuación de flujo de entrada |
| − | | | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (19a) | ||
| + | |} | ||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| − | | | + | | |
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math display="inline">\overset{\cdot}{{q}_{out}}=</math><math>\frac{2{p}_{i}}{L}-\frac{{2p}_{out}}{L}-\frac{2{{R}_{b}P}_{out}}{L}\qquad </math> como ecuación de flujo de salida | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (19b) | ||
| + | |} | ||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" |<math>\overset{\cdot}{{p}_{i}}=\, \frac{4{R}_{di}}{{L}_{i}}{p}_{i}+\, \left( \frac{{2R}_{di}{R}_{b}}{{L}_{i}}-\right. </math><math>\left. \frac{1}{{C}_{i}}\right) {q}_{out}-\left( \frac{1}{{C}_{i}}-\frac{{2R}_{di}{R}_{b}}{{L}_{i}}\right) +</math><math>\frac{{{2R}_{di}p}_{out}}{{L}_{i}}-\frac{{2R}_{di}}{{L}_{i}}{p}_{(i-1)}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (20) | ||
| + | |} | ||
como ecuación de presión. | como ecuación de presión. | ||
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%;" | |
| − | | | + | |- |
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_8995_Fig18.png|center|600px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Figura 18'''. Representación esquemática de la analogía eléctrica en un vaso terminal viscoelástico que fluye hacia capilares | ||
|} | |} | ||
| − | + | La analogía eléctrica que representa el vaso no terminal y el sistema visco elástico presenta la siguiente forma. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | La analogía eléctrica que representa el vaso no terminal y el sistema visco elástico presenta la siguiente forma | + | |
Una vez habiendo tenido claro la estructura del circuito, se definen los parámetros eléctricos que lo componen, tales como el resistor R, la inductancia L, y el condensador C. | Una vez habiendo tenido claro la estructura del circuito, se definen los parámetros eléctricos que lo componen, tales como el resistor R, la inductancia L, y el condensador C. | ||
| − | |||
====3.2.1.3. Parámetros eléctricos==== | ====3.2.1.3. Parámetros eléctricos==== | ||
| − | ''3.2.1.3.1 Resistencia del flujo sanguíneo (R)'' | + | '''''3.2.1.3.1 Resistencia del flujo sanguíneo (R)''''' |
| − | El parámetro '''R '''representa la fuerza de resistencia a la que el fluido está sometido a medida que avanza por el vaso de determinadas características, tales como el diámetro interno del vaso (''d''), su longitud (''l''), entre otros. Un parámetro importante a tener en cuenta en la '''R '''es la viscosidad del fluido, puesto que está presente cuando el fluido es estable u oscilatorio, disipando la energía de éste, aunque el flujo este acelerando o desacelerando. La viscosidad sanguínea que en este caso toma un valor constante de ''µ''=0.004 Pa·s. | + | El parámetro '''R''' representa la fuerza de resistencia a la que el fluido está sometido a medida que avanza por el vaso de determinadas características, tales como el diámetro interno del vaso (''d''), su longitud (''l''), entre otros. Un parámetro importante a tener en cuenta en la '''R''' es la viscosidad del fluido, puesto que está presente cuando el fluido es estable u oscilatorio, disipando la energía de éste, aunque el flujo este acelerando o desacelerando. La viscosidad sanguínea que en este caso toma un valor constante de ''µ''=0.004 Pa·s. |
La resistencia total del flujo''' '''en un segmento concreto se modela mediante resistores y puede calcularse a partir de la ecuación de ''Poiseuille ''(ec.2), que como vimos en apartados anteriores, describe la relación entre la caída de presión, ''Δp ''y el flujo sanguíneo constante y ''q ''a través de un vaso sanguíneo uniforme y rígido. | La resistencia total del flujo''' '''en un segmento concreto se modela mediante resistores y puede calcularse a partir de la ecuación de ''Poiseuille ''(ec.2), que como vimos en apartados anteriores, describe la relación entre la caída de presión, ''Δp ''y el flujo sanguíneo constante y ''q ''a través de un vaso sanguíneo uniforme y rígido. | ||
| Line 804: | Line 867: | ||
Presenta la siguiente ecuación: | Presenta la siguiente ecuación: | ||
| − | <math display="inline">Q=\, \frac{{\Delta p\pi r}^{4}}{8L\mathrm{\mu}}=\frac{\Delta p}{R}</math> donde aislamos ''R'' | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" |<math display="inline">Q=\, \displaystyle\frac{{\Delta p\pi r}^{4}}{8L\mathrm{\mu}}=\frac{\Delta p}{R}</math> | ||
| + | |} | ||
| + | |} | ||
| + | donde aislamos ''R'' | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | <math>R=\, \frac{8l\mathrm{\mu}}{{\pi r}^{4}}</math> | + | | |
| − | | ( | + | {| style="text-align: left; margin:auto;width: 100%;" |
| + | |- | ||
| + | | style="text-align: center;" | <math>R=\, \frac{8l\mathrm{\mu}}{{\pi r}^{4}}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (21) | ||
|} | |} | ||
| + | donde <math display="inline">l</math> es la longitud del vaso, <math display="inline">\mathrm{\mu}</math> la viscosidad sanguínea y <math display="inline">r</math>, el radio interno del vaso. La ecuación presente también es conocida como la ley hidrodinámica de Ohm. Generalmente, '''R '''se obtiene de la ley de ''Poiseuille, ''pero en la práctica esta expresión se denomina ley hidrodinámica de Ohm. Las unidades que se usará con el resistor será en Pa·s·m<sup>-3</sup>. | ||
| − | + | '''''3.2.1.3.2 Complianza del vaso sanguíneo (C)''''' | |
| − | + | ||
| − | ''3.2.1.3.2 Complianza del vaso sanguíneo (C) '' | + | |
Cuando el flujo atraviesa un vaso elástico, el volumen del vaso puede variar. La clave del efecto de capacitancia sobre el flujo en un vaso elástico es que afecta al volumen total del vaso, por lo tanto, la velocidad de flujo en la entrada puede no ser la misma que en la salida debido a la variación de presión. Así pues, la capacidad de la pared de un vaso sanguíneo para expandirse y contraerse con los cambios de presión se conoce como capacitancia o complianza del vaso, '''C'''. La relación entre presión-volumen se puede cuantificar de dos modos. Por una parte, con la capacitancia '''C '''y por otra, con la elasticidad, es decir, el módulo de la elasticidad, <math display="inline">{E}_{v}=</math><math>\, \frac{1}{C}</math>. | Cuando el flujo atraviesa un vaso elástico, el volumen del vaso puede variar. La clave del efecto de capacitancia sobre el flujo en un vaso elástico es que afecta al volumen total del vaso, por lo tanto, la velocidad de flujo en la entrada puede no ser la misma que en la salida debido a la variación de presión. Así pues, la capacidad de la pared de un vaso sanguíneo para expandirse y contraerse con los cambios de presión se conoce como capacitancia o complianza del vaso, '''C'''. La relación entre presión-volumen se puede cuantificar de dos modos. Por una parte, con la capacitancia '''C '''y por otra, con la elasticidad, es decir, el módulo de la elasticidad, <math display="inline">{E}_{v}=</math><math>\, \frac{1}{C}</math>. | ||
| Line 821: | Line 895: | ||
La capacitancia se calcula usando la siguiente ecuación, donde <math display="inline">\Delta V</math> es el cambio de volumen de sangre, y <math display="inline">\Delta p</math> la variación de presión en el segmento, quedando como: | La capacitancia se calcula usando la siguiente ecuación, donde <math display="inline">\Delta V</math> es el cambio de volumen de sangre, y <math display="inline">\Delta p</math> la variación de presión en el segmento, quedando como: | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math>C=\, \frac{\Delta V}{\Delta p}</math> | + | | style="text-align: center;" | <math>C=\, \frac{\Delta V}{\Delta p}</math> |
| − | | ( | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (22) | ||
|} | |} | ||
| + | donde añadimos las propiedades de los vasos sanguíneos siendo <math display="inline">E</math> el módulo de Young y <math display="inline">h</math> el grosor de la pared del vaso, tal que: | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | <math>C=\, \frac{{2\pi r}^{3}l}{Eh}</math> | + | | |
| − | | ( | + | {| style="text-align: left; margin:auto;width: 100%;" |
| + | |- | ||
| + | | style="text-align: center;" |<math>C=\, \frac{{2\pi r}^{3}l}{Eh}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (23) | ||
|} | |} | ||
| + | Las unidades que se usarán con el condensador serán en m<sup>3</sup>·Pa<sup>-1</sup>. | ||
| − | + | '''''3.2.1.3.3 Inercia de la sangre (L)''''' | |
| − | + | ||
| − | ''3.2.1.3.3 Inercia de la sangre (L)'' | + | |
En cada latido del corazón, el fluido se acelera y se desacelera en el tiempo de un modo no inmediato debido a su inercia, '''L.''' | En cada latido del corazón, el fluido se acelera y se desacelera en el tiempo de un modo no inmediato debido a su inercia, '''L.''' | ||
| − | Dicho parámetro relaciona la caída de presión : <math display="inline">\Delta p</math>'' ''con el cambio de caudal <math display="inline">q</math> en un segmento, que se expresa mediante: <math display="inline">\Delta p=</math><math>L\frac{dq}{dt}</math> . | + | Dicho parámetro relaciona la caída de presión : <math display="inline">\Delta p</math>'' ''con el cambio de caudal <math display="inline">q</math> en un segmento, que se expresa mediante: <math display="inline">\Delta p=</math><math>L\frac{dq}{dt}</math>. |
| − | Del mismo modo, el valor numérico de '''L | + | Del mismo modo, el valor numérico de '''L''', se puede obtener utilizando las propiedades de los vasos sanguíneos, aplicando la ley de Newton relativa al movimiento que implica, fuerza ''(F)'', masa ''(m)'' y aceleración donde <math display="inline">a</math>= <math display="inline">\frac{dv}{dt}</math>'' '' y siendo <math display="inline">F</math> =m <math display="inline">\frac{dv}{dt}</math>. |
| − | Partiendo de ahí, se aplica a un vaso de longitud | + | Partiendo de ahí, se aplica a un vaso de longitud, <math display="inline">l</math>: |
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | | + | | |
| − | | | + | {| style="text-align: left; margin:auto;width: 100%;" |
| + | |- | ||
| + | | style="text-align: center;" |<math display="inline">F=\Delta p\cdot A\qquad</math> y <math display="inline">\qquad m= \rho \cdot V</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (24) | ||
|} | |} | ||
| + | donde <math display="inline">A</math> es el área de sección transversal del vaso cilíndrico, <math display="inline">\rho =1050</math> kg/m<sup>3</sup> es la densidad de la sangre y ''V'' es el volumen del fluido que atraviesa ese segmento. Aplicando la definición de flujo volumétrico <math display="inline">q=</math><math>v\cdot A</math>, donde <math display="inline">v</math> es la velocidad en ese tramo, se deriva y se obtiene: | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | | + | | |
| − | + | {| style="text-align: left; margin:auto;width: 100%;" | |
|- | |- | ||
| − | | style="text-align: center;"|<math>\frac{dv}{dt}=\frac{\overset{\cdot}{\, q\, }}{dA}</math> | + | | style="text-align: center;" |<math display="inline">\overset{\cdot}{\, q\, }\displaystyle\frac{dv}{dt}\, A\, , </math> |
| − | | style="text-align: | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (25) | ||
| + | |} | ||
| + | aislamos el diferencial | ||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | |style="text-align: center;"|<math>\frac{dv}{dt}=\frac{\overset{\cdot}{\, q\, }}{dA}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(26) | ||
|} | |} | ||
| − | + | Así, substituyendo <math display="inline">F</math> y <math display="inline">m</math> en la ecuación tal que, | |
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | <math>\Delta p\, A=\, \rho \, V\frac{\, \overset{\cdot}{\, q\, }}{dA}\rightarrow \Delta p=</math><math>\, \frac{\, \rho \, l}{A}\overset{\cdot}{\, q\, },\,</math> | + | | |
| − | | style="text-align: | + | {| style="text-align: left; margin:auto;width: 100%;" |
| + | |- | ||
| + | | style="text-align: center;" | <math>\Delta p\, A=\, \rho \, V\frac{\, \overset{\cdot}{\, q\, }}{dA}\rightarrow \Delta p=</math><math>\, \frac{\, \rho \, l}{A}\overset{\cdot}{\, q\, },\,</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(27) | ||
|} | |} | ||
| + | que como se ha mencionado, '''L ''' es la relación entre <math display="inline">\Delta p</math> y el caudal, quedando finalmente como: | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| − | {| style="width: 100% | + | | |
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math>L=\, \frac{\rho \, l}{\pi \, {r}^{2}}</math> | + | | style="text-align: center;" | <math>L=\, \frac{\rho \, l}{\pi \, {r}^{2}}</math> |
| − | | style="text-align: | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(28) | ||
|} | |} | ||
| − | Las unidades utilizadas con el inductor serán en | + | Las unidades utilizadas con el inductor serán en Kg·m<sup>-4</sup>. |
| − | |||
====3.2.1.4. Condiciones del modelo==== | ====3.2.1.4. Condiciones del modelo==== | ||
| − | ''3.2.1.4.1 Condiciones de bifurcación'' | + | '''''3.2.1.4.1 Condiciones de bifurcación''''' |
La descomposición de segmentos vasculares requiere tener en cuenta la relación entre varios de ellos dentro de una misma red arterial, es decir, la bifurcación de vasos. Por ello, se definen también condiciones de bifurcación tanto para las presiones como para los flujos, quedando la estructura y las ecuaciones algebraicas tal que: | La descomposición de segmentos vasculares requiere tener en cuenta la relación entre varios de ellos dentro de una misma red arterial, es decir, la bifurcación de vasos. Por ello, se definen también condiciones de bifurcación tanto para las presiones como para los flujos, quedando la estructura y las ecuaciones algebraicas tal que: | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | | + | | |
| − | | | + | {| style="text-align: left; margin:auto;width: 100%;" |
|- | |- | ||
| − | | | + | | style="text-align: center;" |<math display="inline">{q}_{3}={q}_{1}+\, {q}_{2},\qquad </math> en fusión de flujo |
| − | | | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (29) | ||
|- | |- | ||
| − | | style="text-align: center;"|<math display="inline">{ | + | | |
| − | + | {| style="text-align: left; margin:auto;width: 100%;" | |
| + | |- | ||
| + | | style="text-align: center;" |<math display="inline">{q}_{1}={q}_{3}+\, {q}_{2},\qquad </math> en divergencia de flujo | ||
|} | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (30) | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" |<math display="inline">{p}_{3}=\, {p}_{1}=\, {p}_{2},</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (31) | ||
| + | |} | ||
| + | en presiones tanto de fusión como divergencia del vaso. | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[Image:Draft_Samper_411837410-image20-c.png|center|426px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
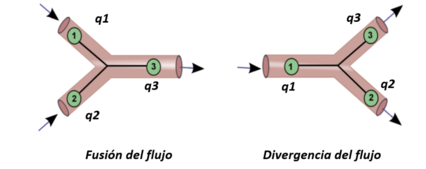
| + | | colspan="1" style="padding-bottom:10px;" | '''Figura 19'''. Representación esquemática de bifurcación de la red arterial | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
Estas ecuaciones se obtienen de la conservación de la masa y del momento, que se traduce en que, la presión siempre será constante y el caudal del flujo debe conservarse en una bifurcación. | Estas ecuaciones se obtienen de la conservación de la masa y del momento, que se traduce en que, la presión siempre será constante y el caudal del flujo debe conservarse en una bifurcación. | ||
| − | Los flujos divergentes se dan a cabo durante la bifurcación de los vasos sanguíneos. De acuerdo a la conservación de masa mencionada, el flujo del nodo 1 sería igual a la suma del flujo del nodo 2 y el nodo 3 ( <math display="inline">{q}_{1}=</math><math>{q}_{3}+\, {q}_{2}</math>), siendo la presión constante en todo el segmento, es decir, la presión de salida en el nodo 1 ha de ser igual a la de entrada del nodo 2 y 3. Del mismo modo ocurre con la conservación de masa en zonas donde el flujo se fusiona, el flujo del nodo 3 ha de ser la suma del flujo del nodo 1 y 2 ( <math display="inline">{q}_{3}=</math><math>{q}_{1}+\, {q}_{2}</math>) y, de acuerdo con la ley de conservación del momento, para este caso la presión total también permanece continua en todos los nodos. | + | Los flujos divergentes se dan a cabo durante la bifurcación de los vasos sanguíneos. De acuerdo a la conservación de masa mencionada, el flujo del nodo 1 sería igual a la suma del flujo del nodo 2 y el nodo 3 (<math display="inline">{q}_{1}=</math><math>{q}_{3}+\, {q}_{2}</math>), siendo la presión constante en todo el segmento, es decir, la presión de salida en el nodo 1 ha de ser igual a la de entrada del nodo 2 y 3. Del mismo modo ocurre con la conservación de masa en zonas donde el flujo se fusiona, el flujo del nodo 3 ha de ser la suma del flujo del nodo 1 y 2 (<math display="inline">{q}_{3}=</math><math>{q}_{1}+\, {q}_{2}</math>) y, de acuerdo con la ley de conservación del momento, para este caso la presión total también permanece continua en todos los nodos. |
| − | ''3.2.1.4.2 Condiciones de salida'' | + | '''''3.2.1.4.2 Condiciones de salida''''' |
La longitud total de los vasos sanguíneos en el sistema cardiovascular humano de una persona adulta es aproximadamente de unos 95.000 kilómetros. Con estas cifras, es prácticamente imposible modelar decenas de miles de capilares de arteriolas y capilares del sistema circulatorio. | La longitud total de los vasos sanguíneos en el sistema cardiovascular humano de una persona adulta es aproximadamente de unos 95.000 kilómetros. Con estas cifras, es prácticamente imposible modelar decenas de miles de capilares de arteriolas y capilares del sistema circulatorio. | ||
| Line 924: | Line 1,039: | ||
Por eso, una solución viable existente es la de agrupar todos los nodos posteriores que componen el sistema arterial, en segmentos terminales. Los capilares son considerados vasos de resistencia, de modo que se usa una resistencia terminal ''R<sub>b</sub>'' para presentar el efecto acumulativo de la microcirculación más allá de los segmentos terminales. Este resistor será constante y presentará un valor de 1.89E+09 Pa·s·m<sup>-3</sup>[4]. | Por eso, una solución viable existente es la de agrupar todos los nodos posteriores que componen el sistema arterial, en segmentos terminales. Los capilares son considerados vasos de resistencia, de modo que se usa una resistencia terminal ''R<sub>b</sub>'' para presentar el efecto acumulativo de la microcirculación más allá de los segmentos terminales. Este resistor será constante y presentará un valor de 1.89E+09 Pa·s·m<sup>-3</sup>[4]. | ||
| − | Además, se aplica una condición de contorno de presión constante, p<sub>out,</sub> conocida como condición de frontera de Dirichlet<span id="fnc-7"></span><span style="text-align: center; font-size: 75%;">[[#fn-7|<sup>7</sup>]]</span>, para la resolución de las ecuaciones diferenciales. Entonces, el valor de p<sub>out </sub>–que se trata de la presión venosa media para calcular el flujo de salida en el límite p<sub>out</sub> -será de 15 mmHg (2000 Pa) | + | Además, se aplica una condición de contorno de presión constante, p<sub>out,</sub> conocida como condición de frontera de Dirichlet<span id="fnc-7"></span><span style="text-align: center; font-size: 75%;">[[#fn-7|<sup>7</sup>]]</span>, para la resolución de las ecuaciones diferenciales. Entonces, el valor de p<sub>out </sub>–que se trata de la presión venosa media para calcular el flujo de salida en el límite p<sub>out</sub> -será de 15 mmHg (2000 Pa) [12]. Este valor, junto con el circuito terminal, se usó igualmente para los cálculos de las ecuaciones diferenciales, aunque el segmento no fuese realmente terminal en el cuerpo humano. |
| − | |||
====3.2.1.5. Resolución numérica==== | ====3.2.1.5. Resolución numérica==== | ||
| Line 933: | Line 1,047: | ||
Además, como para cada bifurcación se deben cumplir las leyes de cantidad y momento y conservación de masa, se añaden al sistema 4 ecuaciones algebraicas más, haciendo un total de 13 ecuaciones. | Además, como para cada bifurcación se deben cumplir las leyes de cantidad y momento y conservación de masa, se añaden al sistema 4 ecuaciones algebraicas más, haciendo un total de 13 ecuaciones. | ||
| − | Debido a que este sistema contiene tanto ecuaciones diferenciales como ordinarias, se obtiene un sistema de ecuaciones algebraicas diferenciales (DAE). Hay que remarcar que, tanto el modelo elástico como el visco elástico, tienen el mismo número de ecuaciones diferenciales y algebraicas, pero con la diferencia, que como se mencionó en el | + | Debido a que este sistema contiene tanto ecuaciones diferenciales como ordinarias, se obtiene un sistema de ecuaciones algebraicas diferenciales (DAE). Hay que remarcar que, tanto el modelo elástico como el visco elástico, tienen el mismo número de ecuaciones diferenciales y algebraicas, pero con la diferencia, que como se mencionó en el Apartado 3.2.1.2, la presión arterial en la salida de cada segmento para el modelo elástico, solo depende de la resistencia terminal, pero para el modelo viscoso, depende de la complianza del vaso (C) y de la resistencia de la arteria. |
El número total de incógnitas será de 13 (presión y caudal de entrada y de salida en cada segmento no terminal, y caudal de entrada, de salida y presión para el segmento terminal), pero debido a que se conoce el caudal en la entrada del sistema en la aorta ascendente –se explicará en apartados siguientes-se obtiene un sistema de 12 ecuaciones con 12 incógnitas. | El número total de incógnitas será de 13 (presión y caudal de entrada y de salida en cada segmento no terminal, y caudal de entrada, de salida y presión para el segmento terminal), pero debido a que se conoce el caudal en la entrada del sistema en la aorta ascendente –se explicará en apartados siguientes-se obtiene un sistema de 12 ecuaciones con 12 incógnitas. | ||
| − | Para poder resolver este sistema de ecuaciones algebraicas diferenciales se necesita definir una matriz de masa. Esta matriz de masa tiene que ser diagonal constante con 1 para las variables diferenciales y 0 para las variables algebraicas, representándose: | + | Para poder resolver este sistema de ecuaciones algebraicas diferenciales se necesita definir una matriz de masa. Esta matriz de masa tiene que ser diagonal constante con 1 para las variables diferenciales y 0 para las variables algebraicas, representándose: <math>M(t,y)y'= f(t,y)</math>, con <math>M(t,y)</math> definida. |
| − | + | Por ejemplo, un sistema DAE con 2 ecuaciones diferenciales y una variable algebraica se expresaría como: | |
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |-style="text-align: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math display="inline">M=\left[ \begin{matrix}1&0&0\\0&1&0\\0&0&0\end{matrix}\right] \quad \quad M\frac{dy}{dx}\left( x,y\right) =</math><math>f\left( x,y\right) \rightarrow \left[ \begin{matrix}\displaystyle\frac{d{y}_{1}}{dx}\\ \displaystyle\frac{d{y}_{2}}{dx}\\0\end{matrix}\right] =</math><math>\left[ \begin{matrix}{f}_{1}(x,{y}_{1},{y}_{2},{y}_{3})\\{f}_{2}(x,{y}_{1},{y}_{2},{y}_{3})\\{f}_{3}(x,{y}_{1},{y}_{2},{y}_{3})\end{matrix}\right]</math> | ||
| + | |} | ||
| − | |||
Por lo tanto, para el modelo desarrollado, la matriz de masa será de [12x8], de los cuales 1 son los primeros 8 elementos de la diagonal que serán igual a 1 y el resto igual a 0 correspondiendo a las ecuaciones algebraicas. Una vez definido la matriz de masa y las ecuaciones diferenciales y algebraicas, se utiliza el método de diferenciación numérica – ode15s – implementado en Matlab [21]. | Por lo tanto, para el modelo desarrollado, la matriz de masa será de [12x8], de los cuales 1 son los primeros 8 elementos de la diagonal que serán igual a 1 y el resto igual a 0 correspondiendo a las ecuaciones algebraicas. Una vez definido la matriz de masa y las ecuaciones diferenciales y algebraicas, se utiliza el método de diferenciación numérica – ode15s – implementado en Matlab [21]. | ||
| Line 965: | Line 1,084: | ||
::* Disección aórtica en sistema visco elástico | ::* Disección aórtica en sistema visco elástico | ||
| − | |||
| − | |||
===4.1. Modelo elástico de la arteria aorta=== | ===4.1. Modelo elástico de la arteria aorta=== | ||
| − | |||
| − | |||
====4.1.1. Parámetros de entrada==== | ====4.1.1. Parámetros de entrada==== | ||
| Line 992: | Line 1,107: | ||
El flujo de sangre que emite el ventrículo hacia la aorta será representado durante el ciclo cardiaco completo-siendo este de 0.8 s- como ''I(t) ''con amplitud <math display="inline">{I}_{0}</math>'' ''durante la sístole, pues durante la diástole, los ventrículos están relajados y no hay flujo emergente, por lo tanto, ''I(t)=0. ''Sin embargo, la contracción ventricular durante el primer periodo, la sangre sí que fluye hacia la aorta definiendo la siguiente ecuación: | El flujo de sangre que emite el ventrículo hacia la aorta será representado durante el ciclo cardiaco completo-siendo este de 0.8 s- como ''I(t) ''con amplitud <math display="inline">{I}_{0}</math>'' ''durante la sístole, pues durante la diástole, los ventrículos están relajados y no hay flujo emergente, por lo tanto, ''I(t)=0. ''Sin embargo, la contracción ventricular durante el primer periodo, la sangre sí que fluye hacia la aorta definiendo la siguiente ecuación: | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | <math>I\left( t\right) ={I}_{0}\mathrm{sin}\,\left( \pi \ast \frac{mod\left( t,{T}_{c}\right) }{{T}_{s}}\right)</math> | + | | |
| − | | ( | + | {| style="text-align: left; margin:auto;width: 100%;" |
| + | |- | ||
| + | | style="text-align: center;" | <math>I\left( t\right) ={I}_{0}\mathrm{sin}\,\left( \pi \ast \frac{mod\left( t,{T}_{c}\right) }{{T}_{s}}\right)</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (32) | ||
|} | |} | ||
| − | + | donde ''t'' es tiempo en segundos, <math display="inline">{T}_{c}</math> es el periodo de ciclo completo en segundos, <math display="inline">{T}_{s}</math> es el período de sístole en segundos, y <math display="inline">mod\left( t,{T}_{c}\right)</math> representa el vector <math display="inline">t</math> divido entre <math display="inline">{T}_{c}</math>. El parámetro <math display="inline">{T}_{s}</math> se ha determina como 2/5 <math display="inline">{T}_{c}</math> de acuerdo a los parámetros dinámicos del ciclo cardiaco. Se establece también, un flujo entrante en el primer latido de 70 cm<sup>3</sup>. | |
| − | + | ||
Usando ésta información obtenemos la constante <math display="inline">{I}_{0}</math> en: | Usando ésta información obtenemos la constante <math display="inline">{I}_{0}</math> en: | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | | + | | |
| − | + | {| style="text-align: left; margin:auto;width: 100%;" | |
|- | |- | ||
| − | | <math>{I}_{0}=\int_{0}^{{T}_{c}}\left( \frac{1}{70}\right) \mathrm{sin}\,\left( \pi \ast \frac{mod\left( t,{T}_{c}\right) }{{T}_{s}}\right) dt</math> | + | | style="text-align: center;" | <math>70=\int_{0}^{{T}_{c}}{I}_{0}\mathrm{sin}\,\left( \pi \ast \frac{mod\left( t,{T}_{c}\right) }{{T}_{s}}\right) dt</math> |
| − | | | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (33) | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" |<math>{I}_{0}=\int_{0}^{{T}_{c}}\left( \frac{1}{70}\right) \mathrm{sin}\,\left( \pi \ast \frac{mod\left( t,{T}_{c}\right) }{{T}_{s}}\right) dt</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (34) | ||
|} | |} | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 50%;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[Image:Draft_Samper_411837410-image21-c.png|center|530px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
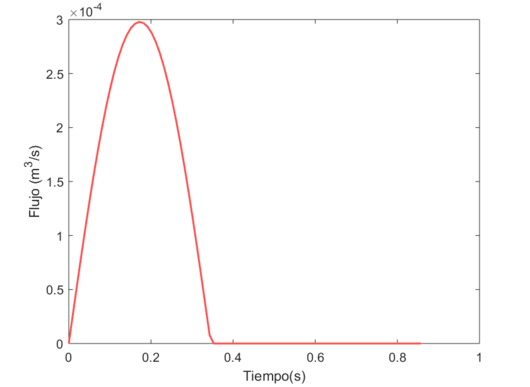
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 1'''. Primer latido simulado del flujo en la entrada de la arteria aorta | ||
| + | |} | ||
| − | |||
| − | |||
| + | Usando el software MATLAB y el código desarrollado, se obtiene que <math display="inline">{I}_{0}=</math><math>297,77\, ml</math> en el bombeo de inyección durante la sístole. Ese será el vector inicial utilizado, ''q<sub>i</sub>.'' | ||
| − | + | Una vez se obtiene el vector de entrada, se debe obtener la presión primera para poner iniciar. Se representa a continuación una pequeña simulación de la presión inicial con la que se emprende el circuito obtenida a partir del flujo de entrada. Se obtienen un total de 20 ciclos cardiacos, de 0,8 segundos cada uno. | |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_4178_Grafica2.png|center|780px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 2'''. Primer parámetro de presión simulado en la entrada de la arteria aorta | ||
| + | |} | ||
| − | |||
| − | |||
| − | Los valores obtenidos en p<sub>in</sub>''' '''se consideran aceptables pues como se aprecia en la | + | Los valores obtenidos en p<sub>in</sub>''' '''se consideran aceptables pues como se aprecia en la Figura 12, se obtienen valores máximos de ± 120 mmHg como presión sistólica, y valores mínimos de ± 80 mmHg como presión diastólica. Los valores fisiológicos reales utilizados de la aorta ascendente obtenidos de para esta iniciación son: |
| + | |||
| + | <div class="center" style="font-size: 75%;">'''Tabla 3'''. Parámetros iniciales | ||
| + | </div> | ||
| − | {| style=" | + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:70%;" |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Nombre'' | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Nombre''' |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Longitud(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Longitud''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Radio(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Radio''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Espesor(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Espesor''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Módulo de Young(Pa) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Módulo de Young''' (Pa) |
| style="border: 1pt solid black;text-align: center;vertical-align: top;"|''P<sub>out</sub>''(Pa) | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''P<sub>out</sub>''(Pa) | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Aorta ascendente |
| style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.06 | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.06 | ||
| style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.01477 | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.01477 | ||
| Line 1,043: | Line 1,181: | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
A partir de estos datos obtenemos los valores eléctricos con las formulas mencionadas en el capítulo tres: | A partir de estos datos obtenemos los valores eléctricos con las formulas mencionadas en el capítulo tres: | ||
| − | {| style=" | + | <div class="center" style="font-size: 75%;">'''Tabla 4'''. Parámetros eléctricos iniciales |
| + | </div> | ||
| + | |||
| + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:70%;" | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''R, | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''R'', '''Resistencia''' (Pa·s·m<sup>-3</sup>) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''L, | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''L'', '''Inductancia''' (kg·m<sup>-4</sup>) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''C, | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''C'', '''Condensador''' (m<sup>3</sup>·Pa<sup>-1</sup>) |
|- | |- | ||
| style="border: 1pt solid black;text-align: center;vertical-align: top;"|1.3088E+04 | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1.3088E+04 | ||
| Line 1,059: | Line 1,197: | ||
| style="border: 1pt solid black;text-align: center;vertical-align: top;"|1.4266E-09 | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1.4266E-09 | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====4.1.2. Inicio de la aorta==== | ====4.1.2. Inicio de la aorta==== | ||
| Line 1,073: | Line 1,206: | ||
Los datos fisiológicos del modelo serán los siguientes: | Los datos fisiológicos del modelo serán los siguientes: | ||
| − | {| style=" | + | <div class="center" style="font-size: 75%;">'''Tabla 5'''. Datos fisiológicos sobre la primera sección de la aorta |
| + | </div> | ||
| + | |||
| + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:80%;" | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"|''Arteria'' | + | | style="border: 1pt solid black;text-align: center;"|'''Arteria''' |
| − | | style="border: 1pt solid black;text-align: center;"|''Longitud(m) | + | | style="border: 1pt solid black;text-align: center;"|'''Longitud''' (m) |
| − | | style="border: 1pt solid black;text-align: center;"|''Radio(m) | + | | style="border: 1pt solid black;text-align: center;"|'''Radio''' (m) |
| − | | style="border: 1pt solid black;text-align: center;"|''Espesor(m) | + | | style="border: 1pt solid black;text-align: center;"|'''Espesor''' (m) |
| − | | style="border: 1pt solid black;text-align: center;"|''Módulo de Young (Pa) | + | | style="border: 1pt solid black;text-align: center;"|'''Módulo de Young''' (Pa) |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Aorta ascendente |
| style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.06 | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.06 | ||
| style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.01477 | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.01477 | ||
| Line 1,087: | Line 1,223: | ||
| style="border: 1pt solid black;text-align: center;vertical-align: top;"|587000 | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|587000 | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Arco aorta |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.02 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.0144 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.00143 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|819000 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Arteria torácica |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.03 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.01355 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.00144 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|994000 |
|} | |} | ||
| − | <div | + | <div class="center" style="font-size: 75%;">'''Tabla 6'''. Datos fisiológicos sobre la primera sección de la aorta |
| − | + | </div> | |
| − | {| style=" | + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:80%;" |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Arteria'' | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Arteria''' |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Resistencia (Pa·s·m<sup>-3</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Resistencia''' (Pa·s·m<sup>-3</sup>) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'' | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Inductancia''' (kg·m<sup>-4</sup>) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'' | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Condensador''' (m<sup>3</sup>·Pa<sup>-1</sup>) |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Aorta ascendente |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1.3088E+04 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|9.1476E+04 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1.4266E-09 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Arco aorta |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|4.7378E+03 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|3.1775E+04 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|3.2039E-10 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Arteria torácica |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|9.0649E+03 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|5.3831E+04 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|3.2752E-09 |
|} | |} | ||
| − | |||
| + | La analogía eléctrica del primer segmento queda tal como muestra la Figura 20. | ||
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | |
| − | + | |- | |
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_3261_Fig20.png|750px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Figura 20'''. Analogía eléctrica simplificada de la aorta<br /> | ||
| + | Fuente: https://es.wikipedia.org/wiki/Arco_a%C3%B3rtico | ||
| + | |} | ||
| − | Se determina en cada segmento, la presión y el flujo del vaso con los datos fisiológicos expuestos en la página anterior. Cabe destacar que, '''q<sub>in</sub>''' | + | |
| + | Se determina en cada segmento, la presión y el flujo del vaso con los datos fisiológicos expuestos en la página anterior. Cabe destacar que, '''q'''<sub>in</sub> y '''p'''<sub>in</sub>, son los vectores calculados al inicio de la sección y que la presión y el flujo que se calculará en el tercer segmento de la aorta torácica, es el que se empleará para la siguiente sección sobre la disección aórtica. | ||
No obstante, hay que tener en cuenta que, en una persona, esta arteria, solo en los inicios presenta varias bifurcaciones, en la aorta ascendente hay dos, la coronaria derecha y coronaria izquierda, y en arco hay 4, subclavia derecha e izquierda y carótida derecha e izquierda. | No obstante, hay que tener en cuenta que, en una persona, esta arteria, solo en los inicios presenta varias bifurcaciones, en la aorta ascendente hay dos, la coronaria derecha y coronaria izquierda, y en arco hay 4, subclavia derecha e izquierda y carótida derecha e izquierda. | ||
| Line 1,142: | Line 1,284: | ||
Lo que se pretende establecer con este modelo, es que, a parte de la funcionalidad del primer latido, la simulación de sección anatómica arterial siguiente sea igual de funcional y recree con la mayor veracidad posible–dentro de lo que los modelos 0-D permiten hacer y representar- las características hemodinámicas de este segmento arterial tan fundamental, como es la aorta. | Lo que se pretende establecer con este modelo, es que, a parte de la funcionalidad del primer latido, la simulación de sección anatómica arterial siguiente sea igual de funcional y recree con la mayor veracidad posible–dentro de lo que los modelos 0-D permiten hacer y representar- las características hemodinámicas de este segmento arterial tan fundamental, como es la aorta. | ||
| + | A continuación, se muestra una gráfica esquemática (Figura 21) [23] de cómo se propaga el flujo (m<sup>3</sup>/s) a través de la aorta durante la primera sístole, en un período de 0.3 segundos aproximadamente–período de eyección-. Siendo un flujo ínfimo al inicio –unos 4.753E-05 m<sup>3</sup>/s-, y va aumentando a medida que avanza la primera fase, alcanzando casi los 0.00025<span id="fnc-8"></span><span style="text-align: center; font-size: 75%;">[[#fn-8|<sup>8</sup>]]</span> m<sup>3</sup>/s. | ||
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | |
| − | {| | + | |
|- | |- | ||
| − | | [[Image:Draft_Samper_411837410-image25-c.png|center|168px]] | + | | style="text-align: center;padding:10px;"| [[Image:Draft_Samper_411837410-image28-c.png|center|168px]] |
| − | | [[Image:Draft_Samper_411837410-image26-c.png|center|180px]] | + | | style="text-align: center;padding:10px;"| [[Image:Draft_Samper_411837410-image25-c.png|center|168px]] |
| + | | style="text-align: center;padding:10px;"| [[Image:Draft_Samper_411837410-image26-c.png|center|180px]] | ||
| + | | style="text-align: center;padding:10px;"| [[Image:Draft_Samper_411837410-image27-c.png|center|78px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="4" style="padding:10px;"| '''Figura 21'''. Representación del flujo aórtico durante la sístole [30] | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Tras graficar, se observa como el flujo a través de esta primera sección no varía prácticamente, puesto que el caudal de entrada ha de igual siempre al de salida, es decir, la cantidad de flujo que sale y entra y atraviesa las arterias ha de mantenerse constante, para asegurar un buen funcionamiento de las funciones corporales y asegurar que el riego sanguíneo –en situaciones sin patologías- llegue a todos los extremos sin excepciones. | Tras graficar, se observa como el flujo a través de esta primera sección no varía prácticamente, puesto que el caudal de entrada ha de igual siempre al de salida, es decir, la cantidad de flujo que sale y entra y atraviesa las arterias ha de mantenerse constante, para asegurar un buen funcionamiento de las funciones corporales y asegurar que el riego sanguíneo –en situaciones sin patologías- llegue a todos los extremos sin excepciones. | ||
| − | El pequeño desfase se podría deber a la propagación de onda a través de los tubos. El flujo máximo que se aprecia en la | + | El pequeño desfase se podría deber a la propagación de onda a través de los tubos. El flujo máximo que se aprecia en la Figura 21, se ve representado en su punto máximo –presión sistólica- en la Gráfica 3. |
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | [[Image:Draft_Samper_411837410- | + | | style="padding:10px;" | [[Image:Draft_Samper_411837410-image29.png|center|444px]] |
| − | | | + | |- style="text-align: center; font-size: 75%;" |
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 3'''. Curvas de flujo del primer segmento de la aorta, indicando el punto máximo | ||
|} | |} | ||
| − | |||
| − | |||
| − | + | Con la presión sanguínea ocurre el mismo fenómeno, debe mantenerse aproximadamente constante a lo largo de todos los vasos arteriales, desde que sale del ventrículo izquierdo, hacia la aorta ascendente, pasando por todo el tronco aórtico y sus ramificaciones hasta los órganos, hasta llegar a las extremidades y los capilares. La propagación de presión sobre todo el sistema arterial durante un latido entero (0.8 segundos aproximadamente) incluyendo sístole y diástole, asumiendo que el latido empieza en sístole, se puede observar simplificado en la Figura 22. | |
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | [[Image:Draft_Samper_411837410- | + | | style="text-align: center;padding:10px;"| [[Image:Draft_Samper_411837410-image32-c.png|center|168px]] |
| − | | [[Image:Draft_Samper_411837410- | + | | style="text-align: center;padding:10px;"| [[Image:Draft_Samper_411837410-image31-c.png|center|174px]] |
| + | | style="text-align: center;padding:10px;"| [[Image:Draft_Samper_411837410-image30-c.png|center|180px]] | ||
| + | | style="text-align: center;padding:10px;"| [[Image:Draft_Samper_411837410-image33-c.png|center|60px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="4" style="padding:10px;"| '''Figura 22'''. Propagación de la presión sanguínea durante la sístole [30] | ||
|} | |} | ||
| − | {| | + | Se puede apreciar como en ambas fases la presión de la sangre se muestra prácticamente constante a través de todo el sistema arterial. En la fase de sístole, el flujo es mayor, con comportamiento creciente, llegando a casi 16500 Pascales (120 mmHg) en los puntos más altos, puesto que es el período de eyección sanguínea y de contracción de los ventrículos (Figura 22). Durante la fase de diástole, donde se produce la dilatación ventricular, la presión sanguínea baja hasta estar entre los 12000 y 10000 Pascales (90-75 mmHg, respectivamente) en los puntos más bajos como las extremidades (Figura 23). |
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| − | | [[Image:Draft_Samper_411837410-image36-c.png|center|168px]] | + | | style="text-align: center;padding:10px;"| [[Image:Draft_Samper_411837410-image35-c.png|center|174px]] |
| − | | [[Image:Draft_Samper_411837410-image33-c1.png|center|60px]] | + | | style="text-align: center;padding:10px;"| [[Image:Draft_Samper_411837410-image34-c.png|center|174px]] |
| + | | style="text-align: center;padding:10px;"| [[Image:Draft_Samper_411837410-image36-c.png|center|168px]] | ||
| + | | style="text-align: center;padding:10px;"| [[Image:Draft_Samper_411837410-image33-c1.png|center|60px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="4" style="padding:10px;"| '''Figura 23'''. Propagación sanguínea durante la diástole [30] | ||
|} | |} | ||
| + | En la Gráfica 4, que se anexa a continuación perteneciente a la primera sección de la aorta, se comprueba que la presión de sangre no varía prácticamente en ninguno de los tres puntos. El desfase presente puede deber a la propagación de la onda de presión a lo largo del tubo. | ||
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | [[Image:Draft_Samper_411837410-image37-c.png|center|342px]] | + | | style="padding:10px;" | [[Image:Draft_Samper_411837410-image37-c.png|center|342px]] |
| − | | | + | |- style="text-align: center; font-size: 75%;" |
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 4'''. Presión en los primeros segmentos de la aorta | ||
|} | |} | ||
| Line 1,232: | Line 1,351: | ||
===4.2. Disección aórtica === | ===4.2. Disección aórtica === | ||
| − | |||
| − | |||
====4.2.1. Patología==== | ====4.2.1. Patología==== | ||
| − | Hoy en día, las patologías aorticas representa un subgrupo muy importante dentro de las enfermedades cardiovasculares y, aunque su prevalencia es limitada, se asocian con una mortalidad muy alta (>50%) [12]. A pesar de las técnicas de diagnóstico actuales y las terapias mejoradas, el manejo y el seguimiento de las disecciones aorticas continúan siendo un desafío en la práctica clínica. La disección aórtica clásica empieza con la formación de una pequeña incisión llamada lágrima –''tear''- en la capa íntima de la arteria, que expone a la capa media siguiente a la presión pulsátil del flujo sanguíneo | + | Hoy en día, las patologías aorticas representa un subgrupo muy importante dentro de las enfermedades cardiovasculares y, aunque su prevalencia es limitada, se asocian con una mortalidad muy alta (>50%) [12]. A pesar de las técnicas de diagnóstico actuales y las terapias mejoradas, el manejo y el seguimiento de las disecciones aorticas continúan siendo un desafío en la práctica clínica. La disección aórtica clásica empieza con la formación de una pequeña incisión llamada lágrima –''tear''- en la capa íntima de la arteria, que expone a la capa media siguiente a la presión pulsátil del flujo sanguíneo (Figura 24). Esto conlleva a una escisión en dirección longitudinal de ésta capa media a lo largo de la pared aórtica causando la disección. Este proceso de disección se extiende impulsado por la fuerza hacia delante del flujo sanguíneo aórtico. |
| − | Por ello, el lumen quedará dividido en dos partes, el canal principal con el verdadero lumen, ''TL'', y el canal falso, fruto de esta patología, ''FL''. En la mayoría de los casos, el TL y el FL se comunican a través del sitio de entrada y de salida. –véase anatomía de una artería en el | + | Por ello, el lumen quedará dividido en dos partes, el canal principal con el verdadero lumen, ''TL'', y el canal falso, fruto de esta patología, ''FL''. En la mayoría de los casos, el TL y el FL se comunican a través del sitio de entrada y de salida. –véase anatomía de una artería en el Apartado 2.4.2. |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 50%;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[Image:Draft_Samper_411837410-image38.png|center|484px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;" | '''Figura 24'''. Disección de la aorta ascendente (izquierda). Imagen de la aorta descendente en una resonancia magnética (centro) y en tomografía (derecha). TL: verdadero lumen. FL: Falso lumen<br /> | ||
| − | + | Fuente: Validation of numerical flow simulations against in vitro phantom measurements in different type B aortic dissection scenarios, 2013 | |
| − | + | |} | |
| − | |||
| − | Los pacientes que lo padecen presentan una alta mortalidad a medio / largo plazo, debido a la dilatación progresiva del tejido de la aorta y su posterior ruptura. En la práctica actual, la predicción del resultado se basa principalmente en la determinación del diámetro aórtico máximo. | + | Los pacientes que lo padecen presentan una alta mortalidad a medio/largo plazo, debido a la dilatación progresiva del tejido de la aorta y su posterior ruptura. En la práctica actual, la predicción del resultado se basa principalmente en la determinación del diámetro aórtico máximo. |
| − | Sin embargo, se ha visto que este parámetro no es un determinante confiable en la progresión y en la ruptura de la aorta, pues variables hemodinámicas como la presión, las condiciones de flujo, la elasticidad de la pared y factores geométricos como la forma de curvatura de la aorta, la sección de comunicación entre falso lumen y verdadero lumen y el tamaño de las lágrimas juegan un papel importante e influyen directamente en el progreso de dilatación del tejido | + | Sin embargo, se ha visto que este parámetro no es un determinante confiable en la progresión y en la ruptura de la aorta, pues variables hemodinámicas como la presión, las condiciones de flujo, la elasticidad de la pared y factores geométricos como la forma de curvatura de la aorta, la sección de comunicación entre falso lumen y verdadero lumen y el tamaño de las lágrimas juegan un papel importante e influyen directamente en el progreso de dilatación del tejido [17]. |
Dentro de esta patología podemos encontrar dos clasificaciones en función de la extensión en la aorta ascendente: | Dentro de esta patología podemos encontrar dos clasificaciones en función de la extensión en la aorta ascendente: | ||
| Line 1,255: | Line 1,376: | ||
:* ''Tipo A'': Se origina en la aorta ascendente y se puede extender hacia todo el tronco de la aorta o se detiene en el arco aórtico. | :* ''Tipo A'': Se origina en la aorta ascendente y se puede extender hacia todo el tronco de la aorta o se detiene en el arco aórtico. | ||
| − | :* | + | :* ''Tipo B'': Se origina en la aorta descendente y rara vez se extiende. No involucra la sección ascendente. |
| − | + | ||
| − | ''Tipo B'': Se origina en la aorta descendente y rara vez se extiende. No involucra la sección ascendente. | + | |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 40%;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[Image:Draft_Samper_411837410-image39.png|center|336px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;" | '''Figura 25'''. Tipos de disección aórtica<br /> | ||
| + | Fuente:https://es.wikipedia.org/wiki/Disecci%C3%B3n_a%C3%B3rtica | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
Así pues, el objetivo será la elaboración de un circuito eléctrico en dimensión 0-D análogo a la estructura arterial para simular el comportamiento del flujo sanguíneo dentro de una disección aórtica. Los datos utilizados para recrear las dimensiones de la arteria y sus extremos son propuestos por Alastruey [4]. | Así pues, el objetivo será la elaboración de un circuito eléctrico en dimensión 0-D análogo a la estructura arterial para simular el comportamiento del flujo sanguíneo dentro de una disección aórtica. Los datos utilizados para recrear las dimensiones de la arteria y sus extremos son propuestos por Alastruey [4]. | ||
| Line 1,274: | Line 1,397: | ||
Los datos fisiológicos de la arteria abdominal y torácica serán los mismos para los tres escenarios y los dos modelos. Presentan los siguientes valores: | Los datos fisiológicos de la arteria abdominal y torácica serán los mismos para los tres escenarios y los dos modelos. Presentan los siguientes valores: | ||
| − | {| style=" | + | <div class="center" style="font-size: 75%;">'''Tabla 7'''. Datos fisiológicos sobre las arterias utilizadas para la simulación |
| + | </div> | ||
| + | |||
| + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:65%;" | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Arteria'' | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Arteria''' |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Longitud(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Longitud''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Radio(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Radio''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Espesor(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Espesor''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Módulo de Young (Pa) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Módulo de Young'''(Pa) |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Arteria torácica |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.03 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.01355 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.00144 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|994000 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Arteria abdominal |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.06 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.00102 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.00127 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1823000 |
|} | |} | ||
| − | < | + | <div class="center" style="font-size: 75%;">'''Tabla 8'''. Parámetros eléctricos obtenidos a partir de los datos fisiológicos de la Tabla 5 |
| + | </div> | ||
| − | {| style=" | + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:65%;" |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Arteria'' | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Arteria''' |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Resistencia (Pa·s·m<sup>-3</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Resistencia''' (Pa·s·m<sup>-3</sup>) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Inductancia (Kg·m<sup>-4</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Inductancia''' (Kg·m<sup>-4</sup>) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Complianza(m<sup>3</sup>·Pa<sup>-1</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Complianza''' (m<sup>3</sup>·Pa<sup>-1</sup>) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''R<sub>d </sub>(Pa·s·m<sup>-3</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''R<sub>d </sub>'' (Pa·s·m<sup>-3</sup>) |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Arteria torácica |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|9.0649E+03 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|5.3831E+04 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|3.2752E-09 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|4.44E+07 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Arteria abdominal |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|5.64611E+04 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1.8999E+05 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1.7279E-10 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|4.17E+06 |
|} | |} | ||
| − | + | El modelo a representar se localiza y se presenta de la siguiente manera (Figura 26). | |
| − | [[Image:Draft_Samper_411837410-image40.png|center|600px]] | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
| − | + | |- | |
| − | + | |style="padding:10px;"| [[Image:Draft_Samper_411837410-image40.png|center|600px]] | |
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 26'''. Analogía virtual en 3D de la disección aórtica del modelo representado | ||
| + | |} | ||
| − | |||
Así pues, los escenarios trabajados serán, | Así pues, los escenarios trabajados serán, | ||
| Line 1,333: | Line 1,462: | ||
:''1. Escenario primero'' | :''1. Escenario primero'' | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[File:Draft_Samper_411837410_2554_Fig27.png|500px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 27'''. Representación de la arteria. Primer escenario | ||
| + | |} | ||
| − | |||
| − | |||
| − | Los datos fisiológicos con los que se simula el modelo tanto elástico como visco elástico del escenario | + | Las condiciones de la segunda situación serán las siguientes: se determinará la presión en el falso y verdadero lumen en la sección proximal y lo mismo para la sección distal. Los diámetros de las lágrimas en este caso serán del mismo tamaño, siendo de 10 mm la primera lágrima y 10 mm la segunda. |
| + | |||
| + | Los datos fisiológicos con los que se simula el modelo tanto elástico como visco elástico del primer escenario y de los demás escenarios de [9] presentan los siguientes valores (Tabla 9). | ||
| + | |||
| + | <div id="_Toc529365968" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Tabla 9'''. Datos fisiológicos del TL y FL en el primer escenario</span></div> | ||
| − | {| style=" | + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:65%;" |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Segmento'' | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Segmento''' |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Longitud(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Longitud''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Radio(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Radio''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Espesor(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Espesor''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Módulo de Young(Pa) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Módulo de Young''' (Pa) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''R<sub>d </sub>(Pa·s·m<sup>-3</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''R<sub>d </sub>'' (Pa·s·m<sup>-3</sup>) |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Verdadero Lumen |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.16 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.008 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.002 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1070 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1.69E+07 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Falso Lumen |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.16 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.01615 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.002 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|2490 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1.69E+07 |
|} | |} | ||
<div id="_Toc529365968" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div id="_Toc529365968" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <span style="text-align: center; font-size: 75%;">'''Tabla | + | <span style="text-align: center; font-size: 75%;">'''Tabla 10'''. Parámetros obtenidos a partir de los datos fisiológicos en el FL y TL en el primer escenario</span></div> |
| − | {| style=" | + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:65%;" |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Segmento'' | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Segmento''' |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Resistencia (Pa·s·m<sup>-3</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Resistencia''' (Pa·s·m<sup>-3</sup>) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Inductancia (Kg·m<sup>-4</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Inductancia''' (Kg·m<sup>-4</sup>) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Complianza(m<sup>3</sup>·Pa<sup>-1</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Complianza''' (m<sup>3</sup>·Pa<sup>-1</sup>) |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Verdadero Lumen |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|8.8532E+04 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|7.9345E+05 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|1.2000E-09 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Falso Lumen |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|5.33056E+03 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|8.3258E-05 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|1.2761E-09 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Ø proximal 10 mm |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|1.9118E+07 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Ø distal 10 mm |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|1.9118E+07 |
|} | |} | ||
| − | |||
| − | |||
| − | |||
:''2. Escenario segundo'' | :''2. Escenario segundo'' | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[File:Draft_Samper_411837410_1156_Fig28.png|500px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 28'''. Representación de la arteria. Segundo escenario | ||
| + | |} | ||
| − | |||
Las condiciones de la segunda situación serán las siguientes; se determinará la presión en el falso y verdadero lumen en la sección proximal y lo mismo para la sección distal. Los diámetros de las lágrimas en este caso serán de 10 mm la primera lágrima y 4 mm la segunda. | Las condiciones de la segunda situación serán las siguientes; se determinará la presión en el falso y verdadero lumen en la sección proximal y lo mismo para la sección distal. Los diámetros de las lágrimas en este caso serán de 10 mm la primera lágrima y 4 mm la segunda. | ||
Los datos fisiológicos con los que se simula el modelo tanto elástico como visco elástico del escenario segundo presentan los siguientes valores: | Los datos fisiológicos con los que se simula el modelo tanto elástico como visco elástico del escenario segundo presentan los siguientes valores: | ||
| − | + | <div id="_Toc529365968" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | |
| + | <span style="text-align: center; font-size: 75%;">'''Tabla 11'''. Datos fisiológicos del TL y FL en el segundo escenario</span></div> | ||
| + | |||
| + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:65%;" | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Segmento'' | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Segmento''' |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Longitud(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Longitud''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Radio(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Radio''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Espesor(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Espesor''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Módulo de Young(Pa) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Módulo de Young''' (Pa) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''R<sub>d </sub>(Pa·s·m<sup>-3</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''R<sub>d </sub>'' (Pa·s·m<sup>-3</sup>) |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Verdadero Lumen |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.16 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.008 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.002 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1070 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1.69E+07 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Falso Lumen |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.16 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.01615 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.002 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1510 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1.69E+07 |
|} | |} | ||
<div id="_Toc529365970" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div id="_Toc529365970" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <span style="text-align: center; font-size: 75%;">'''Tabla | + | <span style="text-align: center; font-size: 75%;">'''Tabla 12'''. Parámetros obtenidos a partir de los datos fisiológicos en el FL y TL en el segundo escenario</span></div> |
| − | {| style=" | + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:65%;" |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Segmento'' | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Segmento''' |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Resistencia (Pa·s·m<sup>-3</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Resistencia''' (Pa·s·m<sup>-3</sup>) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Inductancia (Kg·m<sup>-4</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Inductancia''' (Kg·m<sup>-4</sup>) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Complianza(m<sup>3</sup>·Pa<sup>-1</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Complianza''' (m<sup>3</sup>·Pa<sup>-1</sup>) |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Verdadero Lumen |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|8.8532E+04 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|7.9345E+05 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|'1.2000E-09 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Falso Lumen |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|5.33056E+03 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|8.3258E-05 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|2.1099E-09 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Ø proximal 10 mm |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|1.9118E+07 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Ø distal 4 mm |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|2.9597E+08 |
|} | |} | ||
| − | |||
| − | |||
| − | |||
:''3. Escenario tercero'' | :''3. Escenario tercero'' | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[File:Draft_Samper_411837410_7485_Fig29.png|500px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 29'''. Esquema sobre la arteria en el tercer escenario | ||
| + | |} | ||
| − | |||
Las condiciones de la tercera situación serán las siguientes; se determinará la presión en el falso y verdadero lumen en la sección proximal y lo mismo para la sección distal. Los diámetros de las lágrimas en este caso serán de 4 mm la primera lágrima y 0 mm la segunda, es decir, no habrá segunda lágrima. | Las condiciones de la tercera situación serán las siguientes; se determinará la presión en el falso y verdadero lumen en la sección proximal y lo mismo para la sección distal. Los diámetros de las lágrimas en este caso serán de 4 mm la primera lágrima y 0 mm la segunda, es decir, no habrá segunda lágrima. | ||
Los datos fisiológicos con los que se simula el modelo tanto elástico como visco elástico del escenario primero presentan los siguientes valores: | Los datos fisiológicos con los que se simula el modelo tanto elástico como visco elástico del escenario primero presentan los siguientes valores: | ||
| − | + | <div id="_Toc529365970" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | |
| + | <span style="text-align: center; font-size: 75%;">'''Tabla 13'''. Datos fisiológicos del TL y FL en el tercer escenario</span></div> | ||
| + | |||
| + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:65%;" | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Segmento'' | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Segmento''' |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Longitud(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Longitud''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Radio(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Radio''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Espesor(m) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Espesor''' (m) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Módulo de Young(Pa) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Módulo de Young''' (Pa) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''R<sub>d </sub>(Pa·s·m<sup>-3</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''R<sub>d </sub>'' (Pa·s·m<sup>-3</sup>) |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Verdadero Lumen |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.16 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.008 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.002 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1070 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1.69E+07 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Falso Lumen |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.16 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.01615 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.002 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|3820 |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|1.69E+07 |
|} | |} | ||
<div id="_Toc529365972" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div id="_Toc529365972" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <span style="text-align: center; font-size: 75%;">'''Tabla | + | <span style="text-align: center; font-size: 75%;">'''Tabla 14'''. Parámetros obtenidos a partir de los datos fisiológicos en el FL y TL en el tercer escenario</span></div> |
| − | {| style=" | + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:65%;" |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Segmento'' | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Segmento''' |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Resistencia (Pa·s·m<sup>-3</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Resistencia''' (Pa·s·m<sup>-3</sup>) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Inductancia (Kg·m<sup>-4</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Inductancia''' (Kg·m<sup>-4</sup>) |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|''Complianza(m<sup>3</sup>·Pa<sup>-1</sup>) | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Complianza''' (m<sup>3</sup>·Pa<sup>-1</sup>) |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Verdadero Lumen |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|8.8532E+04 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|7.93451E+05 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|1.20001E-08 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Falso Lumen |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|5.33056E+03' |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|8.32583E-05 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|1.94695E+08 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Ø proximal 4mm |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|2.9597E+08 |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|Ø distal 0 mm |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|infinita |
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====4.2.2. Disección aórtica con modelo elástico==== | ====4.2.2. Disección aórtica con modelo elástico==== | ||
| + | El modelo eléctrico que representará el segmento aórtico patológico se presenta en la Figura 30. | ||
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | |
| − | + | |- | |
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_5966_Fig30.png|650px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Figura 30'''. Modelo elástico de la disección aórtica con los parámetros principales a determinar | ||
| + | |} | ||
| − | |||
| − | El modelo elástico recrea el comportamiento de los vasos como cilindros, rectos y rígidos. Se divide en cuatro segmentos compuestos por circuitos RLC que pretenden simular una disección aórtica en una sección de la aorta descendente. El primer segmento viene con los valores de '''q<sub>in</sub>''' y '''p<sub>in </sub>'''preestablecidos que se explica en el | + | Donde las incógnitas principales serán las presiones en las sección proximal y distal tales como '''P<sub>pTL</sub> '''que equivale a la presión proximal del verdadero lumen (TL), '''P<sub>pFL </sub>'''que es la presión proximal a través del falso lumen (FL), '''P<sub>dTL </sub>'''como presión del TL en la sección distal y finalmente, '''P<sub>dFL</sub>''' que representa la presión distal en el FL. |
| + | |||
| + | El modelo elástico recrea el comportamiento de los vasos como cilindros, rectos y rígidos. Se divide en cuatro segmentos compuestos por circuitos RLC que pretenden simular una disección aórtica en una sección de la aorta descendente. El primer segmento viene con los valores de '''q<sub>in</sub>''' y '''p<sub>in </sub>'''preestablecidos que se explica en el Apartado 4.1.1. | ||
El modelo que pertenece a esta patología se le añaden dos resistencias en paralelo para imitar el comportamiento de las lágrimas. El cambio de diámetro de las lágrimas se verá reflejado en un cambio en el valor de las resistencias que lo definen –véase apartado anterior-. | El modelo que pertenece a esta patología se le añaden dos resistencias en paralelo para imitar el comportamiento de las lágrimas. El cambio de diámetro de las lágrimas se verá reflejado en un cambio en el valor de las resistencias que lo definen –véase apartado anterior-. | ||
| − | La resolución numérica empleada es la mencionada en el | + | La resolución numérica empleada es la mencionada en el Apartado 3.2.1.5, que trata de definir un sistema de ecuaciones diferenciales de primer orden para obtener las variables requeridas. Las ecuaciones que las determinan se presentan de la siguiente manera, |
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | | + | | |
| − | + | {| style="text-align: left; margin:auto;width: 100%;" | |
|- | |- | ||
| − | | <math>\frac{d{p}_{ | + | | style="text-align: center;" | <math>\frac{d{p}_{pTL}}{dt}=\frac{{q}_{1iTL}-{q}_{3outTL}}{{C}_{TL}}</math> |
| − | | | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (35) | ||
|- | |- | ||
| − | | <math>\frac{d{p}_{dTL}}{dt}=\frac{{q}_{5in}-{q}_{5out}}{{C}_{ABD}}</math> | + | | |
| − | | | + | {| style="text-align: left; margin:auto;width: 100%;" |
| + | |- | ||
| + | | style="text-align: center;" | <math>\frac{d{p}_{pFL}}{dt}=\frac{{q}_{2iFL}-{q}_{4outFL}}{{C}_{FL}}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (36) | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\frac{d{p}_{dTL}}{dt}=\frac{{q}_{5in}-{q}_{5out}}{{C}_{ABD}}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (37) | ||
|} | |} | ||
| − | |||
La presión restante se calculará mediante la ecuación algebraica, | La presión restante se calculará mediante la ecuación algebraica, | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math>{p}_{dFL}=\, {q}_{4outFL}\cdot {R}_{DT}-{p}_{dTL}</math> | + | | style="text-align: center;" | <math>{p}_{dFL}=\, {q}_{4outFL}\cdot {R}_{DT}-{p}_{dTL}</math> |
| − | | ( | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (38) | ||
|} | |} | ||
| − | El parámetro <math display="inline">{R}_{DT}</math> es la resistencia específica para la lágrima en la sección distal. En estas ecuaciones, cada presión viene determinada indirectamente por los valores de flujo calculados en cada segmento | + | El parámetro <math display="inline">{R}_{DT}</math> es la resistencia específica para la lágrima en la sección distal. En estas ecuaciones, cada presión viene determinada indirectamente por los valores de flujo calculados en cada segmento (Figura 29). |
| − | + | ||
| − | + | ||
====4.2.3. Disección aórtica con modelo visco elástico ==== | ====4.2.3. Disección aórtica con modelo visco elástico ==== | ||
| + | A diferencia del modelo elástico, el modelo visco elástico añade una resistencia extra (R<sub>d</sub>) en serie con el condensador para cuantificar la viscoelasticidad del vaso. El modelo eléctrico se representa en el siguiente esquema. | ||
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | |
| − | + | |- | |
| + | | style="padding:10px;" |[[File:Draft_Samper_411837410_5601_Fig31.png|650px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Figura 31'''. Modelo viscoelástico de la disección aórtica con los parámetros principales a determinar | ||
| + | |} | ||
| − | |||
| − | El primer segmento también viene con los valores de '''q<sub>in</sub>''' | + | De igual modo que en la Figura 30, las incógnitas principales serán las presiones en las sección proximal y distal, '''P<sub>pTL</sub>, P<sub>pFL </sub>'''que son las presiones proximales a través del verdadero (TL) y falso lumen (FL) respectivamente, '''P<sub>dTL </sub>'''como presión del TL en la sección distal y, '''P<sub>dFL</sub>''' que representa la presión distal en el FL. |
| + | |||
| + | El primer segmento también viene con los valores de '''q'''<sub>in</sub> y '''p'''<sub>in </sub> preestablecidos obtenidos del Apartado 4.1.1. | ||
A parte de las dos resistencias que simulan las lágrimas, presenta la resistencia '''R<sub>d</sub>,''' añadida en serie al condensador, para recrear un modelo de orden reducido con propiedades visco elásticas. La importancia de añadir este resistor extra se encuentra en el hecho de que el comportamiento de la onda de presión que se obtiene, sea más real y que capture algunos comportamientos fisiológicos, como, por ejemplo, la muesca dicrota. | A parte de las dos resistencias que simulan las lágrimas, presenta la resistencia '''R<sub>d</sub>,''' añadida en serie al condensador, para recrear un modelo de orden reducido con propiedades visco elásticas. La importancia de añadir este resistor extra se encuentra en el hecho de que el comportamiento de la onda de presión que se obtiene, sea más real y que capture algunos comportamientos fisiológicos, como, por ejemplo, la muesca dicrota. | ||
| Line 1,579: | Line 1,748: | ||
También, al suponer que la pared será más distensible, el pico máximo de la onda será más tardío respecto al elástico. El valor de esta resistencia se obtiene de [12] y varía según la sección, es decir, la aorta torácica tiene una, la abdominal otra, y la parte de aorta descendente en la que se aplica el modelo de la disección aórtica, tanto para el FL como el TL tendrán otra –en este caso se llama '''R<sub>d </sub>as '''la perteneciente a la de la disección aórtica, y '''R<sub>d </sub>ab, '''la que se emplea para la aorta abdominal''' '''-. | También, al suponer que la pared será más distensible, el pico máximo de la onda será más tardío respecto al elástico. El valor de esta resistencia se obtiene de [12] y varía según la sección, es decir, la aorta torácica tiene una, la abdominal otra, y la parte de aorta descendente en la que se aplica el modelo de la disección aórtica, tanto para el FL como el TL tendrán otra –en este caso se llama '''R<sub>d </sub>as '''la perteneciente a la de la disección aórtica, y '''R<sub>d </sub>ab, '''la que se emplea para la aorta abdominal''' '''-. | ||
| − | Las ecuaciones, también resultas mediante el método mencionado en el | + | Las ecuaciones, también resultas mediante el método mencionado en el Apartado 3.2.1.5, que rigen la presión especificada en este modelo, se expresan como, |
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | | + | | |
| − | + | {| style="text-align: left; margin:auto;width: 100%;" | |
|- | |- | ||
| − | | <math>\frac{d{p}_{ | + | | style="text-align: center;" | <math>\frac{d{p}_{pTL}}{dt}=\frac{{R}_{d}as}{{L}_{TL}}{p}_{in}+\, \left( \frac{1}{{C}_{TL}}-\right. </math><math>\left. \frac{{R}_{d}{as\cdot R}_{TL}}{{L}_{TL}}\right) {q}_{1iTL}-\frac{{q}_{3outTL}}{{C}_{TL}}-</math><math>\frac{{R}_{d}as}{{L}_{TL}}{p}_{pTL}</math> |
| − | | | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (39) | ||
|- | |- | ||
| − | | <math>\frac{d{p}_{dTL}}{dt}=\frac{{R}_{d}ab}{{L}_{ABD}}{p}_{dFL}+\, \left( \frac{1}{{C}_{ABD}}-\right. </math><math>\left. \frac{{R}_{d}ab\cdot {R}_{ABD}}{{L}_{ABD}}\right) {q}_{5in}-\frac{{q}_{5out}}{{C}_{ABD}}-</math><math>\frac{{R}_{d}ab}{{L}_{ABD}}{p}_{dTL}</math> | + | | |
| − | + | {| style="text-align: left; margin:auto;width: 100%;" | |
| − | + | |- | |
| − | | | + | | style="text-align: center;" | <math>\frac{d{p}_{pFL}}{dt}=\frac{{R}_{d}as}{{L}_{FL}}{p}_{pTL}+\, \left( \frac{1}{{C}_{FL}}-\right. </math><math>\left. \frac{{R}_{d}{as\cdot R}_{FL}}{{L}_{FL}}\right) {q}_{2iFL}-\frac{{q}_{4outFL}}{{C}_{FL}}-</math><math>\frac{{R}_{d}as}{{L}_{FL}}{p}_{pFL}</math> |
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (40) | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\frac{d{p}_{dTL}}{dt}=\frac{{R}_{d}ab}{{L}_{ABD}}{p}_{dFL}+\, \left( \frac{1}{{C}_{ABD}}-\right. </math><math>\left. \frac{{R}_{d}ab\cdot {R}_{ABD}}{{L}_{ABD}}\right) {q}_{5in}-\frac{{q}_{5out}}{{C}_{ABD}}-</math><math>\frac{{R}_{d}ab}{{L}_{ABD}}{p}_{dTL}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (41) | ||
|} | |} | ||
| + | y como ecuación algebraica restante aplicando las leyes de Kirchhoff, | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| − | {| style="width: 100%; | + | | |
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math>{p}_{dFL}=\, {q}_{4outFL}\cdot {R}_{DT}-{p}_{dTL}</math> | + | | style="text-align: center;" | <math>{p}_{dFL}=\, {q}_{4outFL}\cdot {R}_{DT}-{p}_{dTL}</math> |
| − | | ( | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (42) | ||
|} | |} | ||
| − | El parámetro <math display="inline">{R}_{DT}</math> es la resistencia específica para la lágrima en la sección distal. En estas ecuaciones, cada presión viene determinada indirectamente por los valores de flujo calculados en cada segmento | + | El parámetro <math display="inline">{R}_{DT}</math> es la resistencia específica para la lágrima en la sección distal. En estas ecuaciones, cada presión viene determinada indirectamente por los valores de flujo calculados en cada segmento (Figura 30). |
| − | + | ||
| − | + | ||
===4.3. Resultados === | ===4.3. Resultados === | ||
Con los modelos mencionados anteriormente, se exponen los resultados obtenidos tras su evaluación en distintas circunstancias. Primeramente, se representa el modelo visco elástico con varias modificaciones del módulo de Young, para ver cómo evoluciona la onda de presión en función del valor de su rigidez. Por otro lado, se someterá a este mismo modelo a una comparación cualitativa con el modelo experimental [9] y finalmente se mostrarán los modelos elástico y visco elástico conjuntamente, para resaltar las diferentes y similitudes, y remarcar la importancia de la variación de la forma de onda que presenta cada modelo. A esta sección se le añadirá una pequeña comparación cualitativa, mediante el cálculo del coeficiente de variación entre ambas ondas. | Con los modelos mencionados anteriormente, se exponen los resultados obtenidos tras su evaluación en distintas circunstancias. Primeramente, se representa el modelo visco elástico con varias modificaciones del módulo de Young, para ver cómo evoluciona la onda de presión en función del valor de su rigidez. Por otro lado, se someterá a este mismo modelo a una comparación cualitativa con el modelo experimental [9] y finalmente se mostrarán los modelos elástico y visco elástico conjuntamente, para resaltar las diferentes y similitudes, y remarcar la importancia de la variación de la forma de onda que presenta cada modelo. A esta sección se le añadirá una pequeña comparación cualitativa, mediante el cálculo del coeficiente de variación entre ambas ondas. | ||
| − | |||
| − | |||
====4.3.1. Variación del módulo de Young del modelo visco elástico==== | ====4.3.1. Variación del módulo de Young del modelo visco elástico==== | ||
| − | : | + | :'''''I. Escenario primero <math>\phi p= 10</math> mm, <math>\phi d= 10</math> mm)''''' |
El valor E de referenia es de 1070 Pascales en el TL. Se ha expuesto el sistema al doble, con 2140 Pascales y a la mitad, 530 Pascales. Para el falso lumen, la E de referencia es de 2490 Pascales, el máximo de 4980 Pascales, y el mínimo de 1250 Pascales, tanto para la sección proximal y distal. | El valor E de referenia es de 1070 Pascales en el TL. Se ha expuesto el sistema al doble, con 2140 Pascales y a la mitad, 530 Pascales. Para el falso lumen, la E de referencia es de 2490 Pascales, el máximo de 4980 Pascales, y el mínimo de 1250 Pascales, tanto para la sección proximal y distal. | ||
| − | :'' | + | :''a. Sección proximal'' |
| − | + | ||
| − | + | ||
| − | : | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" |
| + | |- | ||
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_2405_Grafica5.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 5'''. Presión en el FL variando el módulo de Young. Sección proximal | ||
| + | |} | ||
| − | {| | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" |
|- | |- | ||
| − | | [[ | + | | style="padding:10px;" | [[File:Draft_Samper_411837410_8358_Grafica6.png|564px]] |
| − | | | + | |- style="text-align: center; font-size: 75%;" |
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 6'''. Presión en el TL variando el módulo de Young. Sección proximal | ||
|} | |} | ||
| − | : | + | :''b. Sección distal'' |
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_7298_Grafica7.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 7'''. Presión en el FL variando el módulo de Young. Sección distal | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_5160_Grafica8.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 8'''. Presión en el TL variando el módulo de Young. Sección distal | ||
| + | |} | ||
| + | |||
| + | |||
| + | :'''''II. Escenario segundo <math>\phi p= 10</math> mm, <math>\phi d= 4</math> mm)''''' | ||
| + | |||
El valor E de referencia es de 1070 Pascales. Se ha expuesto el sistema al doble, con 2140 Pascales y a la mitad, 530 Pascales, en el caso del verdadero lumen. Para el falso lumen, la E de referencia es de 1510 Pascales, el máximo de 3020 Pascales, y el mínimo de 750 Pascales, para la sección proximal y distal. | El valor E de referencia es de 1070 Pascales. Se ha expuesto el sistema al doble, con 2140 Pascales y a la mitad, 530 Pascales, en el caso del verdadero lumen. Para el falso lumen, la E de referencia es de 1510 Pascales, el máximo de 3020 Pascales, y el mínimo de 750 Pascales, para la sección proximal y distal. | ||
| − | :'' | + | :''c. Sección proximal'' |
| − | + | ||
| − | + | ||
| − | : | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" |
| − | [[ | + | |- |
| − | '' | + | | style="padding:10px;" |[[File:Draft_Samper_411837410_5719_Grafica9.png|564px]] |
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 9'''. Presión en el TL variando el módulo de Young. Seccion distal | ||
| + | |} | ||
| − | [[ | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" |
| + | |- | ||
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_2653_Grafica10.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 10'''. Presión en el FL variando el módulo de Young. Seccion distal | ||
| + | |} | ||
| + | |||
| + | |||
| + | :''d. Sección distal'' | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" |[[File:Draft_Samper_411837410_1320_Grafica11.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 11'''. Presión en el FL variando el módulo de Young. Sección distal | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_8290_Grafica12.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 12'''. Presión en el TL variando el módulo de Young. Sección distal | ||
| + | |} | ||
| + | |||
| + | |||
| + | :'''''III. Escenario tercero <math>\phi p= 4</math> mm, <math>\phi d= 0</math> mm)''''' | ||
| − | |||
El valor E de referenia es de 1070 Pascales. Se ha expuesto el sistema al doble, con 2140 Pascales y a la mitad, 530 Pascales, en el caso del verdadero lumen. Para el falso lumen, la E de referencia es de 3910 Pascales, el máximo de 7640 Pascales, y el mínimo de 1910 Pascales, para la sección proximal y distal. | El valor E de referenia es de 1070 Pascales. Se ha expuesto el sistema al doble, con 2140 Pascales y a la mitad, 530 Pascales, en el caso del verdadero lumen. Para el falso lumen, la E de referencia es de 3910 Pascales, el máximo de 7640 Pascales, y el mínimo de 1910 Pascales, para la sección proximal y distal. | ||
| − | : | + | :''e. Sección proximal '' |
| − | + | ||
| − | ''Sección proximal '' | + | |
| − | : | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" |
| + | |- | ||
| + | | style="padding:10px;" |[[File:Draft_Samper_411837410_8787_Grafica13.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 13'''. Presión en el FL variando el módulo de Young. Sección proximal | ||
| + | |} | ||
| − | [[ | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" |
| + | |- | ||
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_5786_Grafica14.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 14'''. Presión en el TL variando el módulo de Young. Sección distal | ||
| + | |} | ||
| + | |||
| + | |||
| + | :''f. Sección distal'' | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" |[[File:Draft_Samper_411837410_9123_Grafica15.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 15'''. Presión en el FL variando el módulo de Young. Sección distal | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_1247_Grafica16.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 16'''. Presión en el TL variando el módulo de Young. Sección distal | ||
| + | |} | ||
| + | |||
El objetivo de alterar el módulo de Young (E) predefinido por otros valores, es la observación del efecto de la elasticidad en la pared arterial en el verdadero y falso lumen y ver las variaciones que se producen en las curvas. Tras observar las gráficas, se puede definir que, un aumento del valor del módulo elástico en el vaso, se traduce a un vaso con mayor rigidez. Este hecho se plasma en un pico de onda más elevado y una presión ligeramente mayor. A la inversa, si E disminuye, el vaso es más deformable y la onda tiene una presión menor. | El objetivo de alterar el módulo de Young (E) predefinido por otros valores, es la observación del efecto de la elasticidad en la pared arterial en el verdadero y falso lumen y ver las variaciones que se producen en las curvas. Tras observar las gráficas, se puede definir que, un aumento del valor del módulo elástico en el vaso, se traduce a un vaso con mayor rigidez. Este hecho se plasma en un pico de onda más elevado y una presión ligeramente mayor. A la inversa, si E disminuye, el vaso es más deformable y la onda tiene una presión menor. | ||
| Line 1,668: | Line 1,922: | ||
Cabe destacar que, la diferencia de la forma de onda entre el TL y el FL se debe al caudal, es decir, el TL presenta un caudal mayor respecto al segundo. Esto puede verse reflejado puesto que en las ondas del TL se aprecian mejor características hemodinámicas destacables, como la muesca dicrota. La onda del FL es más suave y redondeada porque el flujo que lo atraviesa es mucho menor y cuesta percibir alguna característica destacable. | Cabe destacar que, la diferencia de la forma de onda entre el TL y el FL se debe al caudal, es decir, el TL presenta un caudal mayor respecto al segundo. Esto puede verse reflejado puesto que en las ondas del TL se aprecian mejor características hemodinámicas destacables, como la muesca dicrota. La onda del FL es más suave y redondeada porque el flujo que lo atraviesa es mucho menor y cuesta percibir alguna característica destacable. | ||
| − | |||
| − | |||
====4.3.2. Comparación del modelo visco elástico versus modelo experimental==== | ====4.3.2. Comparación del modelo visco elástico versus modelo experimental==== | ||
| Line 1,677: | Line 1,929: | ||
El modelo experimental se realizó ''in vitro'' –los datos con los que trabajan también son experimentales- sobre un sistema elástico, recreando una disección aórtica con un ''phantom'' de látex. Se espera observar similitudes significativas como la propagación de onda, valores parecidos de presiones en el FL y TL y cierta similitud con el comportamiento de la onda, teniendo en cuenta que la comparación se realiza desde un modelo visco elástico y la forma de onda que éste presenta. | El modelo experimental se realizó ''in vitro'' –los datos con los que trabajan también son experimentales- sobre un sistema elástico, recreando una disección aórtica con un ''phantom'' de látex. Se espera observar similitudes significativas como la propagación de onda, valores parecidos de presiones en el FL y TL y cierta similitud con el comportamiento de la onda, teniendo en cuenta que la comparación se realiza desde un modelo visco elástico y la forma de onda que éste presenta. | ||
| − | Algunos de los datos con los se ha recreado el sistema visco elástico, -módulo de Young para el TL y el FL en cada escenario y las resistencias que representan las lágrimas-fueron recogidas de este modelo experimental. Sin embargo, los parámetros de entrada que se usaron en cada caso eran diferentes, puesto que en el caso del modelo visco elástico del trabajo, '''q<sub>in</sub>''' | + | Algunos de los datos con los se ha recreado el sistema visco elástico, -módulo de Young para el TL y el FL en cada escenario y las resistencias que representan las lágrimas-fueron recogidas de este modelo experimental. Sin embargo, los parámetros de entrada que se usaron en cada caso eran diferentes, puesto que en el caso del modelo visco elástico del trabajo, '''q'''<sub>in</sub> y '''p'''<sub>in </sub> eran calculadas mediante una senoide, y en el modelo ''in vitro'' fueron obtenidas experimentalmente. |
| − | : | + | :'''''I. Escenario primero (<math>\phi p= 10</math> mm, <math>\phi d= 10</math> mm)''''' |
| + | |||
| + | :''a. Sección proximal'' | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" |[[File:Draft_Samper_411837410_2684_Grafica17.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 17'''. Curva de presión en modelo viscoelástico. sección proximal. Primer escenario | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_4609_Grafica18.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;" | '''Gráfica 18'''. Curva de presión en el modelo elástico experimental. sección proximal. Primer escenario | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
La evaluación de la primera onda en la parte proximal, muestran claras similitudes. Aunque las ondas son ciertamente diferentes, se puede apreciar como ambas curvas empiezan bajo el mismo comportamiento. Empiezan alrededor de unos 80 mmHg, yendo la presión del TL en cabeza respecto al FL. En el período de crecimiento de onda, ambos casos se separan notablemente, volviéndose a unir en el punto máximo, llegando a la par a unos 120 mmHg. | La evaluación de la primera onda en la parte proximal, muestran claras similitudes. Aunque las ondas son ciertamente diferentes, se puede apreciar como ambas curvas empiezan bajo el mismo comportamiento. Empiezan alrededor de unos 80 mmHg, yendo la presión del TL en cabeza respecto al FL. En el período de crecimiento de onda, ambos casos se separan notablemente, volviéndose a unir en el punto máximo, llegando a la par a unos 120 mmHg. | ||
| Line 1,689: | Line 1,955: | ||
En la onda visco elástica se muestra el cierre de la válvula aórtica –muesca dicrota-, mientras que, en el modelo elástico experimental, esa característica fisiológica no se representa. Al decrecer la onda, en ambos casos los valores de presión del TL y el FL son muy semejantes y se unifican en una sola línea. | En la onda visco elástica se muestra el cierre de la válvula aórtica –muesca dicrota-, mientras que, en el modelo elástico experimental, esa característica fisiológica no se representa. Al decrecer la onda, en ambos casos los valores de presión del TL y el FL son muy semejantes y se unifican en una sola línea. | ||
| − | :'' | + | :''b. Sección distal'' |
| − | + | ||
| − | [[ | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 65%;" |
| + | |- | ||
| + | | style="padding:10px;" |[[File:Draft_Samper_411837410_5484_Grafica19.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;" | '''Gráfica 19'''. Curva de presión en modelo viscoelástico. sección distal. Primer escenario | ||
| + | |} | ||
| − | |||
| − | [[ | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 65%;" |
| − | '' | + | |- |
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_5670_Grafica20.png|450px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;" | '''Gráfica 20'''. Curva de presión en modelo experimental. sección distal. Primer escenario | ||
| + | |} | ||
| − | |||
| − | + | En esta sección distal, se aprecia primeramente como la onda de presión del FL de salida es mayor respecto al TL. Durante el crecimiento de la onda, las dos presiones se cruzan, llegando al punto máximo de presión en ambas curvas al mismo instante. –aproximadamente en el segundo 12,3-Durante el período de decrecimiento, la curva del FL se adelanta hasta llegar a su punto más bajo y muestra un área bajo la curva ligeramente más extensa que TL. Cabe decir que respecto el comportamiento general, no se observa apenas desfase de onda entre el FL y TL en ninguno de los dos modelos. | |
| + | |||
| + | :'''''II. Escenario segundo (<math>\phi p= 10</math> mm, <math>\phi d= 4</math> mm)''''' | ||
| + | |||
| + | :''c. Sección proximal'' | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" |[[File:Draft_Samper_411837410_6990_Grafica21.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;" | '''Gráfica 21'''. Curva de presión en modelo viscoelástico. sección proximal. Segundo escenario | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_6273_Grafica22.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;" | '''Gráfica 22'''. Curva de presión en modelo experimental. sección proximal. Segundo escenario | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
En el segundo escenario la curva del falso lumen inicia en un valor mayor respecto al verdadero lumen. Inmediatamente se cruzan, siendo el verdadero lumen el que aumenta más rápidamente. Al llegar casi al punto máximo de presión, se vuelven a cruzar intercambiando papeles. El falso lumen alcanza una presión mayor en ambos casos. Se aprecia suavemente un leve salto durante el decrecimiento de las ondas, que pertenece a la incisura dicrota. Se atisba un pequeño desfase de onda en ambos casos, con el falso lumen por delante respecto al verdadero lumen. Durante el decrecimiento perteneciente a la fase de sístole, el TL disminuye más rápidamente. | En el segundo escenario la curva del falso lumen inicia en un valor mayor respecto al verdadero lumen. Inmediatamente se cruzan, siendo el verdadero lumen el que aumenta más rápidamente. Al llegar casi al punto máximo de presión, se vuelven a cruzar intercambiando papeles. El falso lumen alcanza una presión mayor en ambos casos. Se aprecia suavemente un leve salto durante el decrecimiento de las ondas, que pertenece a la incisura dicrota. Se atisba un pequeño desfase de onda en ambos casos, con el falso lumen por delante respecto al verdadero lumen. Durante el decrecimiento perteneciente a la fase de sístole, el TL disminuye más rápidamente. | ||
| Line 1,711: | Line 1,999: | ||
La variación entre los valores de presión entre el FL y el TL puede deberse simplemente a una cuestión numérica durante la resolución de las ecuaciones diferenciales que componen el sistema. Como se ha especificado en otros apartados, se representan las lágrimas con resistencias. Según el tamaño de la lágrima el valor de dicha resistencia varia. En este caso, como ambas lágrimas poseen diámetros diferentes, la resistencia con la que se trabajará también será diferente, y en este caso, el resistor que representa la lágrima de 10 mm es menor que la de 4 mm, quedando R<sub>10 </sub>< R<sub>4</sub>. Por ese motivo, como el cálculo de la presión del falso lumen depende de estas variables indirectamente, puede haber sido un factor que haya hecho que aumente la presión en esa sección. | La variación entre los valores de presión entre el FL y el TL puede deberse simplemente a una cuestión numérica durante la resolución de las ecuaciones diferenciales que componen el sistema. Como se ha especificado en otros apartados, se representan las lágrimas con resistencias. Según el tamaño de la lágrima el valor de dicha resistencia varia. En este caso, como ambas lágrimas poseen diámetros diferentes, la resistencia con la que se trabajará también será diferente, y en este caso, el resistor que representa la lágrima de 10 mm es menor que la de 4 mm, quedando R<sub>10 </sub>< R<sub>4</sub>. Por ese motivo, como el cálculo de la presión del falso lumen depende de estas variables indirectamente, puede haber sido un factor que haya hecho que aumente la presión en esa sección. | ||
| − | : | + | :''d. Sección distal'' |
| − | + | ||
| − | [[ | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" |
| + | |- | ||
| + | | style="padding:10px;" |[[File:Draft_Samper_411837410_9092_Grafica23.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;" | '''Gráfica 23'''. Curva de presión en modelo viscoelástico. sección distal. Segundo escenario | ||
| + | |} | ||
| − | |||
| − | [[ | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" |
| − | '' | + | |- |
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_6407_Grafica24.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;" | '''Gráfica 24'''. Curva de presión en modelo experimental. sección distal. Segundo escenario | ||
| + | |} | ||
| + | |||
En este caso, las ondas tanto del FL como el TL de cada modelo, salen desde el mismo valor prácticamente, y enseguida cada una toma su camino. La onda del TL crece a mayor velocidad llegando a su punto máximo apenas un poco antes que el FL. Antes de llegar a la presión sistólica, se cruzan y la onda del FL crece brevemente por encima del TL. En el caso viscoso, el FL sigue un comportamiento lineal decreciente, mientras que el TL muestra de un modo muy leve una pequeña protuberancia, indicando la presencia del inciso dicroto. Durante este decrecimiento las curvas se acercan bastante hasta su presión mínima. | En este caso, las ondas tanto del FL como el TL de cada modelo, salen desde el mismo valor prácticamente, y enseguida cada una toma su camino. La onda del TL crece a mayor velocidad llegando a su punto máximo apenas un poco antes que el FL. Antes de llegar a la presión sistólica, se cruzan y la onda del FL crece brevemente por encima del TL. En el caso viscoso, el FL sigue un comportamiento lineal decreciente, mientras que el TL muestra de un modo muy leve una pequeña protuberancia, indicando la presencia del inciso dicroto. Durante este decrecimiento las curvas se acercan bastante hasta su presión mínima. | ||
| Line 1,725: | Line 2,021: | ||
La variación entre los valores de presión entre el FL y el VL puede deberse a una cuestión numérica durante la resolución de las ecuaciones diferenciales que componen el sistema, como se ha explicado en el apartado anterior dedicado a la sección proximal. | La variación entre los valores de presión entre el FL y el VL puede deberse a una cuestión numérica durante la resolución de las ecuaciones diferenciales que componen el sistema, como se ha explicado en el apartado anterior dedicado a la sección proximal. | ||
| − | : | + | :'''''III. Escenario tercero <math>\phi p= 4</math> mm, <math>\phi d= 0</math> mm''''' |
| − | : | + | :''e. Sección proximal'' |
| − | + | ||
| − | [[ | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;;" |
| + | |- | ||
| + | | style="padding:10px;" |[[File:Draft_Samper_411837410_9621_Grafica25.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;" | '''Gráfica 25'''. Curva de presión en modelo viscoelástico. sección proximal. Tercer escenario | ||
| + | |} | ||
| − | |||
| − | [[Image:Draft_Samper_411837410- | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" |
| − | '' | + | |- |
| + | | style="padding:10px;" | [[Image:Draft_Samper_411837410-image65.png|center|414px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;" | '''Gráfica 26'''. Curva de presión en modelo experimental. sección proximal. Tercer escenario | ||
| + | |} | ||
| + | |||
En este último escenario, cabe destacar que la curva del FL no se puede comparar debido a un error en la medida por parte del modelo experimental. Se podría mencionar que el TL del modelo viscoso empieza con una presión superior respecto al falso lumen. También, que en el modelo del trabajo se capta a la perfección la mencionada incisura dicrota, mientras que en el otro no se aprecia apenas, hecho que podría ser una ventaja del modelo viscoso puesto que es capaz de simular con más exactitud características fisiológicas. | En este último escenario, cabe destacar que la curva del FL no se puede comparar debido a un error en la medida por parte del modelo experimental. Se podría mencionar que el TL del modelo viscoso empieza con una presión superior respecto al falso lumen. También, que en el modelo del trabajo se capta a la perfección la mencionada incisura dicrota, mientras que en el otro no se aprecia apenas, hecho que podría ser una ventaja del modelo viscoso puesto que es capaz de simular con más exactitud características fisiológicas. | ||
| Line 1,743: | Line 2,047: | ||
Se empleó una ''R'' de un valor a la orden de E+38. Al emplear un número tan elevado, posiblemente incrementó los valores de las variables en ecuaciones para calcular la presión en el TL. | Se empleó una ''R'' de un valor a la orden de E+38. Al emplear un número tan elevado, posiblemente incrementó los valores de las variables en ecuaciones para calcular la presión en el TL. | ||
| − | : | + | :''f. Sección distal'' |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" |[[File:Draft_Samper_411837410_5190_Grafica27.png|564px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;" | '''Gráfica 27'''. Curva de presión en modelo viscoelástico. sección distal. Tercer escenario | ||
| + | |} | ||
| − | {| | + | |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
|- | |- | ||
| − | | [[ | + | | style="padding:10px;" | [[File:Draft_Samper_411837410_2628_Grafica28.png|center|360px]] |
| − | | | + | |- style="text-align: center; font-size: 75%;" |
| + | | colspan="1" style="padding:10px;" | '''Gráfica 28'''. Curva de presión en modelo experimental. sección distal. Tercer escenario | ||
|} | |} | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
En la sección distal, las ondas obtenidas en ambos modelos presentan un comportamiento semejante. Se observa al principio como la onda del FL es mayor respecto a la otra. Justo después, se cruzan ambas, siendo la del TL que crece más rápidamente. Ambas muestran una separación considerable, debido al desfase de onda de pulso –FL desfasada hacia delante respecto a TL-. | En la sección distal, las ondas obtenidas en ambos modelos presentan un comportamiento semejante. Se observa al principio como la onda del FL es mayor respecto a la otra. Justo después, se cruzan ambas, siendo la del TL que crece más rápidamente. Ambas muestran una separación considerable, debido al desfase de onda de pulso –FL desfasada hacia delante respecto a TL-. | ||
| − | Tras alcanzar su punto más alto, sobre unos 120 mmHg, donde se vuelven a cruzar, ambas decrecen sin tocarse hasta su presión mínima de unos 80 mmHg. Durante el decrecimiento se puede observar como en los dos modelos se refleja una pequeña ondulación de la onda de presión perteneciente a una leve representación del cierre de la válvula aórtica | + | Tras alcanzar su punto más alto, sobre unos 120 mmHg, donde se vuelven a cruzar, ambas decrecen sin tocarse hasta su presión mínima de unos 80 mmHg. Durante el decrecimiento se puede observar como en los dos modelos se refleja una pequeña ondulación de la onda de presión perteneciente a una leve representación del cierre de la válvula aórtica –justo entre los 12,4 y 12,5 segundos-. Se observa de un modo más pronunciado en el modelo visco elástico. |
''Cabe destacar que, en todos los casos, los modelos presentaban rangos de presión razonable, siendo aproximadamente 120 mmHg de presión sistólica, y 80-85 mmHg de presión diastólica. El comportamiento genérico se comparte entre ambos, la onda crece, llegando a su máximo de presión, y decrece, llegando a su mínimo. '' | ''Cabe destacar que, en todos los casos, los modelos presentaban rangos de presión razonable, siendo aproximadamente 120 mmHg de presión sistólica, y 80-85 mmHg de presión diastólica. El comportamiento genérico se comparte entre ambos, la onda crece, llegando a su máximo de presión, y decrece, llegando a su mínimo. '' | ||
| − | |||
| − | |||
====4.3.3. Comparación modelo del elástico versus visco elástico obtenidos==== | ====4.3.3. Comparación modelo del elástico versus visco elástico obtenidos==== | ||
| − | En este apartado se procederá a realizar un análisis cuantitativo de los modelos visco elástico y elásticos, elaborados en este trabajo, para comparar como afecta la viscoelasticidad del vaso a la forma de onda de presión, equiparando el comportamiento de ambos modelos. Se representarán las presiones pertenecientes del verdadero y falso lumen, tanto de la sección distal, como de la proximal. Los datos fisiológicos de ambos modelos se han recogido de [4 | + | En este apartado se procederá a realizar un análisis cuantitativo de los modelos visco elástico y elásticos, elaborados en este trabajo, para comparar como afecta la viscoelasticidad del vaso a la forma de onda de presión, equiparando el comportamiento de ambos modelos. Se representarán las presiones pertenecientes del verdadero y falso lumen, tanto de la sección distal, como de la proximal. Los datos fisiológicos de ambos modelos se han recogido de [4,9,12]. |
Hay recordar que, el modelo elástico utilizado en dimensiones 0-D representa la arteria como un vaso cilíndrico, recto y uniformes, sin tener en cuenta ningún parámetro que registre la distensibilidad del vaso, por lo que se espera que las curvas que se obtengan presenten un comportamiento lineal, sin saltos ni variaciones significativas a lo largo de la curva. | Hay recordar que, el modelo elástico utilizado en dimensiones 0-D representa la arteria como un vaso cilíndrico, recto y uniformes, sin tener en cuenta ningún parámetro que registre la distensibilidad del vaso, por lo que se espera que las curvas que se obtengan presenten un comportamiento lineal, sin saltos ni variaciones significativas a lo largo de la curva. | ||
| − | Con diferencia, el modelo visco elástico, incorpora esa resistencia extra en serie con el condensador –explicada en el | + | Con diferencia, el modelo visco elástico, incorpora esa resistencia extra en serie con el condensador –explicada en el Apartado 4.2.3- que pretende representar la acumulación de energía de la pared del vaso durante el paso del flujo sanguíneo, intentando mostrar un comportamiento lo más real posible al comportamiento natural del vaso. Con esto, se espera que las ecuaciones que rigen el modelo visco elástico, muestren una curva un poco menos lineal, con algunas variaciones hemodinámicas significativas como la incisura dicrota, la propagación de onda y/o el rebote de la onda, entre otros. |
| − | A parte, se realiza también una comparativa cuantitativa, calculando el coeficiente de variación ( <math display="inline">{C}_{V}</math>). Este parámetro estadístico, hace referencia a la relación entre el tamaño de la media y la variabilidad de la variable. El coeficiente de variación se calcula mediante la expresión, | + | A parte, se realiza también una comparativa cuantitativa, calculando el coeficiente de variación (<math display="inline">{C}_{V}</math>). Este parámetro estadístico, hace referencia a la relación entre el tamaño de la media y la variabilidad de la variable. El coeficiente de variación se calcula mediante la expresión, |
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | | + | | |
| − | | | + | {| style="text-align: left; margin:auto;width: 100%;" |
| + | |- | ||
| + | | style="text-align: center;" | <math display="inline">{C}_{V}=\frac{{\sigma }^{\ast }}{\left| \overline{x}\right| }\cdot 100</math>. | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (43) | ||
|} | |} | ||
| Line 1,783: | Line 2,094: | ||
Esta fórmula presenta la relación entre la desviación estándar de una muestra <math display="inline">{\sigma }^{\ast }</math>, y su media <math display="inline">\overline{x}</math>, permitiendo así comparar dispersiones de diferentes distribuciones. Generalmente, no dispone de unidades, pero se puede representar en tanto por cien, para tener una idea más clara de lo que se está comparando. Así pues, como más grande sea el valor obtenido por el coeficiente de variación, más dispersión presenta la distribución, que se traduce a una mayor diferencia entre los valores, y a su vez, las ondas. Esta dispersión <math display="inline">{\sigma }^{\ast }</math> y la media <math display="inline">\overline{x},\,</math> se calculan, | Esta fórmula presenta la relación entre la desviación estándar de una muestra <math display="inline">{\sigma }^{\ast }</math>, y su media <math display="inline">\overline{x}</math>, permitiendo así comparar dispersiones de diferentes distribuciones. Generalmente, no dispone de unidades, pero se puede representar en tanto por cien, para tener una idea más clara de lo que se está comparando. Así pues, como más grande sea el valor obtenido por el coeficiente de variación, más dispersión presenta la distribución, que se traduce a una mayor diferencia entre los valores, y a su vez, las ondas. Esta dispersión <math display="inline">{\sigma }^{\ast }</math> y la media <math display="inline">\overline{x},\,</math> se calculan, | ||
| − | {| style="width: 100%; | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
|- | |- | ||
| − | | | + | | |
| − | | | + | {| style="text-align: left; margin:auto;width: 100%;" |
|- | |- | ||
| − | | | + | | style="text-align: center;" | <math display="inline">{\sigma }^{\ast }=\sqrt{\frac{\sum _{i}^{}{({x}_{i}-\overline{x})}^{2}}{n}}</math>. |
| − | | | + | |} |
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (44) | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math display="inline">\overline{x}=\frac{\sum _{i}^{}{x}_{i}}{n}</math>, | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (45) | ||
|} | |} | ||
| + | siendo <math display="inline">n</math> el número total de muestras. | ||
| − | : | + | :'''''I. Escenario primero <math>\phi p= 10</math> mm, <math>\phi d= 10</math> mm)''''' |
| − | + | ====4.3.3.1. Presión. Primer escenario==== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | {| style="width: | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"|Sección | + | | style="padding:10px;" |[[File:Draft_Samper_411837410_8356_Grafica29.png|564px]] |
| − | | style="border: 1pt solid black;text-align: center;"|''Coeficiente de Variación (C<sub>v</sub>) entre el modelo elástico y viscoelàstico | + | |- style="text-align: center; font-size: 75%;" |
| + | | colspan="1" style="padding:10px;" | '''Gráfica 29'''. Comparativa de presión entre modelo visco elástico y elástico. sección distal. Primer escenario | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_2645_Grafica30.png|center|360px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;" | '''Gráfica 30'''. Comparativa de presión entre modelo visco elástico y elástico. sección proximal. Primer escenario | ||
| + | |} | ||
| + | |||
| + | |||
| + | <div class="center" style="font-size: 75%;">'''Tabla 15'''. Coeficiente de variación entre ambos modelos. Primer escenario | ||
| + | </div> | ||
| + | |||
| + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:65%;" | ||
| + | |- | ||
| + | | style="border: 1pt solid black;text-align: center;"|'''Sección''' | ||
| + | | style="border: 1pt solid black;text-align: center;"|'''Coeficiente de Variación''' (C<sub>v</sub>) entre el modelo elástico y viscoelàstico | ||
|- | |- | ||
| style="border: 1pt solid black;text-align: center;"|Sección proximal TL | | style="border: 1pt solid black;text-align: center;"|Sección proximal TL | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|12.9% |
|- | |- | ||
| style="border: 1pt solid black;text-align: center;"|Sección proximal FL | | style="border: 1pt solid black;text-align: center;"|Sección proximal FL | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|2.2% |
|- | |- | ||
| style="border: 1pt solid black;text-align: center;"|Sección distal TL | | style="border: 1pt solid black;text-align: center;"|Sección distal TL | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|14.1% |
|- | |- | ||
| style="border: 1pt solid black;text-align: center;"|Sección distal FL | | style="border: 1pt solid black;text-align: center;"|Sección distal FL | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|4.9% |
|} | |} | ||
| − | + | Las diferencias apreciables a primera vista del modelo visco elástico y elástico, es el comportamiento de la onda de cada uno. El primero, la onda refleja más expansión, el área bajo su curva es considerablemente mayor respecto al otro. (Tanto para el TL como para el FL) Se diferencia claramente la incisura dicrota en la sección proximal. Este modelo llega a su presión sistólica máxima de un modo más tardío respecto al modelo contrario, e incluso el pico máximo es menor. Esto hecho es un comportamiento razonable y esperado, que se explicó en el Apartado 4.3.1. | |
| − | + | ||
| − | Las diferencias apreciables a primera vista del modelo visco elástico y elástico, es el comportamiento de la onda de cada uno. El primero, la onda refleja más expansión, el área bajo su curva es considerablemente mayor respecto al otro. (Tanto para el TL como para el FL) Se diferencia claramente la incisura dicrota en la sección proximal. Este modelo llega a su presión sistólica máxima de un modo más tardío respecto al modelo contrario, e incluso el pico máximo es menor. Esto hecho es un comportamiento razonable y esperado, que se explicó en el | + | |
En el caso del elástico, la curva evoluciona de un modo lineal, llegando a su punto máximo y decreciendo sin nada apreciable. Ocurre lo mismo para la sección distal. El comportamiento lineal del modelo elástico está vigente, pues la onda crece y decrece más rápidamente que el modelo viscoso. | En el caso del elástico, la curva evoluciona de un modo lineal, llegando a su punto máximo y decreciendo sin nada apreciable. Ocurre lo mismo para la sección distal. El comportamiento lineal del modelo elástico está vigente, pues la onda crece y decrece más rápidamente que el modelo viscoso. | ||
| Line 1,827: | Line 2,161: | ||
Respecto a los coeficientes de variación calculados, observamos que las ondas del TL son las que más presentan diferencia, alcanzando un valor de casi un 14%. Por el contrario, el FL presenta unas variaciones muy pequeñas, apenas llegando al 5%. Con esto, se podría valorar que las curvas se asemejan ciertamente, pues al tener una variación de aproximadamente 14%, significa que en un 86% si se muestran parecidas. No obstante, el comportamiento de la curva si es diferente, pues capta de un modo más claro, parámetros fisiológicos destacables. | Respecto a los coeficientes de variación calculados, observamos que las ondas del TL son las que más presentan diferencia, alcanzando un valor de casi un 14%. Por el contrario, el FL presenta unas variaciones muy pequeñas, apenas llegando al 5%. Con esto, se podría valorar que las curvas se asemejan ciertamente, pues al tener una variación de aproximadamente 14%, significa que en un 86% si se muestran parecidas. No obstante, el comportamiento de la curva si es diferente, pues capta de un modo más claro, parámetros fisiológicos destacables. | ||
| − | : | + | :'''''II. Escenario segundo <math>\phi p= 10</math> mm, <math>\phi d= 4</math> mm)''''' |
| − | + | ====4.3.3.2. Presión. Segundo escenario==== | |
| − | ====4.3.3.2. Presión. Segundo escenario | + | |
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | |
| − | {| | + | |
|- | |- | ||
| − | | [[ | + | | style="padding:10px;" |[[File:Draft_Samper_411837410_4348_Grafica31.png|564px]] |
| − | | | + | |- style="text-align: center; font-size: 75%;" |
| + | | colspan="1" style="padding:10px;" | '''Gráfica 31'''. Comparativa de presión entre modelo visco elástico y elástico. Sección distal. Segundo escenario | ||
|} | |} | ||
| − | {| | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" |
|- | |- | ||
| − | | [[ | + | | style="padding:10px;" | [[File:Draft_Samper_411837410_2176_Grafica32.png|center|360px]] |
| − | | | + | |- style="text-align: center; font-size: 75%;" |
| + | | colspan="1" style="padding:10px;" | '''Gráfica 32'''. Comparativa de presión entre modelo visco elástico y elástico. Sección proximal. Segundo escenario | ||
|} | |} | ||
| − | |||
| + | <div class="center" style="font-size: 75%;">'''Tabla 16'''. Coeficiente de variación entre ambos modelos. Segundo escenario | ||
| + | </div> | ||
| − | + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:75%;" | |
| − | + | ||
| − | {| style=" | + | |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"|Sección | + | | style="border: 1pt solid black;text-align: center;"|'''Sección''' |
| − | | style="border: 1pt solid black;text-align: center;"|''Coeficiente de Variación (C<sub>v</sub>) entre el modelo elástico y viscoelàstico'' | + | | style="border: 1pt solid black;text-align: center;"|'''Coeficiente de Variación''' (C<sub>v</sub>) '''entre el modelo elástico y viscoelàstico''' |
|- | |- | ||
| style="border: 1pt solid black;text-align: center;"|Sección proximal TL | | style="border: 1pt solid black;text-align: center;"|Sección proximal TL | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|20.1% |
|- | |- | ||
| style="border: 1pt solid black;text-align: center;"|Sección proximal FL | | style="border: 1pt solid black;text-align: center;"|Sección proximal FL | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|1.8% |
|- | |- | ||
| style="border: 1pt solid black;text-align: center;"|Sección distal TL | | style="border: 1pt solid black;text-align: center;"|Sección distal TL | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|10.5% |
|- | |- | ||
| style="border: 1pt solid black;text-align: center;"|Sección distal FL | | style="border: 1pt solid black;text-align: center;"|Sección distal FL | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|1.7% |
|} | |} | ||
| − | + | En el segundo escenario, ocurre igual que en el primero. Destaca el modelo visco elástico delante del elástico por el comportamiento de la onda. En este caso, la muesca dicrota se aprecia incluso más que en el caso anterior. Este modelo sigue presentando un área bajo la curva mayor respecto al otro, un punto máximo de presión que se alcanza más tarde (Gráfica 31), como el modelo elástico alcanza su presión sistólica máxima en los 12,23 segundos aproximadamente, y el modelo viscoso la alcanza en el punto 12,3 segundos. El comportamiento del modelo elástico se mantiene lineal en ambas secciones. Se captan en ambos modelos la propagación de la onda de pulso, siendo un poco menor, en el caso del modelo viscoso. | |
| − | + | ||
| − | En el segundo escenario, ocurre igual que en el primero. Destaca el modelo visco elástico delante del elástico por el comportamiento de la onda. En este caso, la muesca dicrota se aprecia incluso más que en el caso anterior. Este modelo sigue presentando un área bajo la curva mayor respecto al otro, un punto máximo de presión que se alcanza más tarde | + | |
Tanto en la sección proximal como distal, la curva del FL del primer modelo es muy parecida a la del segundo modelo. Se observa por eso, que el coeficiente de variación entre ambas no llega al 2%. El verdadero lumen en cambio, presenta una variación un poco mayor, puesto que la forma de la onda es bastante diferente. | Tanto en la sección proximal como distal, la curva del FL del primer modelo es muy parecida a la del segundo modelo. Se observa por eso, que el coeficiente de variación entre ambas no llega al 2%. El verdadero lumen en cambio, presenta una variación un poco mayor, puesto que la forma de la onda es bastante diferente. | ||
| − | : | + | :'''III. Escenario tercero <math>\phi p= 4</math> mm, <math>\phi d= 0</math> mm)''''' |
| − | |||
====4.3.3.3. Presión. Tercer escenario==== | ====4.3.3.3. Presión. Tercer escenario==== | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
| + | |- | ||
| + | | style="padding:10px;" | [[File:Draft_Samper_411837410_3910_Grafica33.png]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;" | '''Figura 33'''. Comparativa de presión entre modelo visco elástico y elástico. sección distal. Tercer escenario | ||
| + | |} | ||
| − | {| | + | |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto;" | ||
|- | |- | ||
| − | | [[ | + | | style="padding:10px;" | [[File:Draft_Samper_411837410_4602_Grafica34.png]] |
| − | | | + | |- style="text-align: center; font-size: 75%;" |
| + | | colspan="1" style="padding:10px;" | '''Figura 34'''. Comparativa de presión entre modelo visco elástico y elástico. sección proximal. Tercer escenario | ||
|} | |} | ||
| − | |||
| − | {| style="width: | + | <div class="center" style="font-size: 75%;">'''Tabla 17'''. Coeficiente de variación entre ambos modelos. Tercer escenario |
| + | </div> | ||
| + | |||
| + | {| style="width: 65%;margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;" | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"|Sección | + | | style="border: 1pt solid black;text-align: center;width:150px;"|'''Sección''' |
| − | | style="border: 1pt solid black;text-align: center;"|''Coeficiente de Variación (C<sub>v</sub>) entre el modelo elástico y viscoelàstico'' | + | | style="border: 1pt solid black;text-align: center;width:400px;"|'''Coeficiente de Variación (C<sub>v</sub>) entre el modelo elástico y viscoelàstico''' |
|- | |- | ||
| style="border: 1pt solid black;text-align: center;"|Sección proximal TL | | style="border: 1pt solid black;text-align: center;"|Sección proximal TL | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|25.7% |
|- | |- | ||
| style="border: 1pt solid black;text-align: center;"|Sección proximal FL | | style="border: 1pt solid black;text-align: center;"|Sección proximal FL | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|6.3% |
|- | |- | ||
| style="border: 1pt solid black;text-align: center;"|Sección distal TL | | style="border: 1pt solid black;text-align: center;"|Sección distal TL | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|15.7% |
|- | |- | ||
| style="border: 1pt solid black;text-align: center;"|Sección distal FL | | style="border: 1pt solid black;text-align: center;"|Sección distal FL | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|10.7% |
|} | |} | ||
| − | |||
| − | |||
| − | |||
Las curvas de presión obtenidas en la sección proximal en el modelo elástico muestran un comportamiento lineal, una curva bien definida, sin apenas alteraciones. Se aprecia por un lado, el punto de presión sistólica –punto máximo- y el de presión diastólica –punto mínimo- tanto en el TL como en el FL, y por otro, hay un desfase pronunciado entre la onda del TL y el FL representando la propagación de onda del fluido. | Las curvas de presión obtenidas en la sección proximal en el modelo elástico muestran un comportamiento lineal, una curva bien definida, sin apenas alteraciones. Se aprecia por un lado, el punto de presión sistólica –punto máximo- y el de presión diastólica –punto mínimo- tanto en el TL como en el FL, y por otro, hay un desfase pronunciado entre la onda del TL y el FL representando la propagación de onda del fluido. | ||
| Line 1,918: | Line 2,255: | ||
Los valores de presión que presentan se consideran normales, pues oscilan entre 125 mmHg de máximo y unos 80 mmHg de mínimo. | Los valores de presión que presentan se consideran normales, pues oscilan entre 125 mmHg de máximo y unos 80 mmHg de mínimo. | ||
| − | Al observar los valores obtenidos por el ''C<sub>v </sub>'' vemos que hay cierta simulitud entre la sección distal y proximal del FL en ambos modelos (±entre 6% y 11%) , y que esta disminuye al tratarse del TL, pues el valor es mucho mayor ( | + | Al observar los valores obtenidos por el ''C<sub>v </sub>'' vemos que hay cierta simulitud entre la sección distal y proximal del FL en ambos modelos (±entre 6% y 11%) , y que esta disminuye al tratarse del TL, pues el valor es mucho mayor (± entre 26% y 16%). Con esto, podría valorar que las curvas se asemejan ciertamente, pues al tener una variación de aproximadamente el 20%, significa que en un 80% si se muestran se parecen. |
| − | Tras la comparación de ambos modelos en los diferentes escenarios se observa un comportamiento similar dentro de cada modelo específico. En cada caso, la presión oscilaba entre los 120 mmHg como máximo y unos 80 como mínimo. En el caso del tercer escenario que la presión máxima y mínima se ve ligeramente alterada, se menciona la posible causa. (véase | + | Tras la comparación de ambos modelos en los diferentes escenarios se observa un comportamiento similar dentro de cada modelo específico. En cada caso, la presión oscilaba entre los 120 mmHg como máximo y unos 80 como mínimo. En el caso del tercer escenario que la presión máxima y mínima se ve ligeramente alterada, se menciona la posible causa. (véase Apartado 4.3.2., Sección e) Finiquitando esta sección y la parte de resultados, cabe resaltar que se han obstenidos los resultados esperados en cuanto al comportamiento del sistema siendo este elástico o viscoso. |
| − | + | ||
| − | + | ||
==Conclusiones== | ==Conclusiones== | ||
| Line 1,959: | Line 2,294: | ||
Como se ha comentado anteriormente una de las dificultades del trabajo fue el ajuste de los variables del modelo, para ello como trabajo futuro, se podría realizar un ajuste/análisis paramétrico de las mismas utilizando medidas reales de los pacientes. Se podría implementar un método de optimización para minimizar una función objetivo entre los datos reales (flujo o presión del paciente) y el simulado (modelo 0D), de manera de obtener las características fisiológicas del paciente más aproximadas. | Como se ha comentado anteriormente una de las dificultades del trabajo fue el ajuste de los variables del modelo, para ello como trabajo futuro, se podría realizar un ajuste/análisis paramétrico de las mismas utilizando medidas reales de los pacientes. Se podría implementar un método de optimización para minimizar una función objetivo entre los datos reales (flujo o presión del paciente) y el simulado (modelo 0D), de manera de obtener las características fisiológicas del paciente más aproximadas. | ||
| − | |||
| − | |||
==Bibliografía== | ==Bibliografía== | ||
| − | [1] A.Quarteroni and L.Formaggia. Mathematical modelling and numerical simulation of the cardiovascular system. 2002. | + | [1] A. Quarteroni and L. Formaggia. Mathematical modelling and numerical simulation of the cardiovascular system. 2002. |
| − | [2] Caro | + | [2] C.G. Caro, T.J. Pedley, R.C. Schroter and W.A. Seed. ''The mechanics of the circulation''. Oxford University Press, 1978. |
| − | [3] I.Kokalari, T.Karaja, and M.Guerrisi. ''Review on lumped parameter method for modeling the blood flow in systemic arteries. J. Biomedical Science and Engineering'', 2013. | + | [3] I. Kokalari, T. Karaja, and M. Guerrisi. ''Review on lumped parameter method for modeling the blood flow in systemic arteries. J. Biomedical Science and Engineering'', 2013. |
[4] J. Alastruey. ''Numerical modelling of pulse wave propagation in the cardiovascular system development, validation and clinical application''. PhD thesis, Imperial College London, 2006. | [4] J. Alastruey. ''Numerical modelling of pulse wave propagation in the cardiovascular system development, validation and clinical application''. PhD thesis, Imperial College London, 2006. | ||
| Line 1,974: | Line 2,307: | ||
[5] Williams & Warwick. ''Gray’s anatomy''. 36th edition edition, 1980. | [5] Williams & Warwick. ''Gray’s anatomy''. 36th edition edition, 1980. | ||
| − | [6] L.Formaggia, A.Quarteroni, and A.Veneziani''. Cardiovascular mathematics: Modeling and simulation of the circulatory system''. 2009. | + | [6] L. Formaggia, A. Quarteroni, and A. Veneziani''. Cardiovascular mathematics: Modeling and simulation of the circulatory system''. 2009. |
| − | [7] J.D.Humphrey. The cardiovascular system''. Biomechanics of Soft Tissue in Cardiovascular Systems,'' CISM(441), 2001. | + | [7] J.D. Humphrey. The cardiovascular system''. Biomechanics of Soft Tissue in Cardiovascular Systems,'' CISM(441), 2001. |
| − | [8] P. Segers, A. Qasem, T. De Backer, S. Carlier, P. Verdonck | + | [8] P. Segers, A. Qasem, T. De Backer, S. Carlier, P. Verdonck and A. Avolio. ''Peripheral ‘oscillatory’ compliance is associated with aortic augmentation index''. Hypertension, 2001. |
| − | [9] P.Rudenick, B.Bijnens, | + | [9] P. Rudenick, B. Bijnens, P. Segers, A. Evangelista. ''Assesment of Wall Elasticity Variation on Intraluminal Haemodynamics in Descending Aortic Dissections Using a Lumped-Parameter Model.'' 2015. |
| − | [10] J. Wan, B. Steele, S.A. Spicer, S. Strohband, T.J.R. Hughes | + | [10] J. Wan, B. Steele, S.A. Spicer, S. Strohband, T.J.R. Hughes and C.A. Taylor. A one-dimensional finite element method for simulation-based medical planning for cardiovascular disease. Comp. Meths. Biomech. Biomed. Eng., 5(3), 195-206, 2002. |
| − | [11] | + | [11] P.A. Rudenick, M. Bordone, B.H. Bijnens, E. Soudah, E. Oñate, D. Garcia-Dorado and A. Evangelista''. Influence of tear configuration on false and true lumen haemodynamics in type B aortic dissection, 2015.'' |
| − | [12] R.Gul. ''Mathematical Modeling and Sensitivity Analysis of Lumped-Parameter Model of the Human Cardiovascular System''. PhD thesis , 2016. | + | [12] R. Gul. ''Mathematical Modeling and Sensitivity Analysis of Lumped-Parameter Model of the Human Cardiovascular System''. PhD thesis, 2016. |
| − | [13] Noordergraaf | + | [13] Noordergraaf A., Verdouw P.D. and Boom H.B.K. ''The use of an analog computer in a circulation model. Progress in Cardiovascular Disease''s, 1963. |
| − | [14] | + | [14] C.D. Prevel, MD, Hani S. ''The extrinsic blood supply of the ulnar nerve at the elbow: An anatomic study.'' Journal of Hand Surgery Am., 18(3), 433-8, 1993. |
| − | [15] Phillips | + | [15] Phillips C., ''A simple lumped parameter model of the cardiovascular system''. PhD thesis, Colorado State University Fort Collins, Colorado, 2011. |
| − | [16] Soudah | + | [16] Soudah E., Rudenick P., Bordone M., Bijnens B., García-Dorado D., Evangelista A. and Oñate, E. Validation of numerical flow simulations against in vitro phantom measurements in different type B aortic dissection scenarios. ''Computer methods in biomechanics and biomedical engineering'', 8(8), 805-815, 2015. |
| − | [17] Rudenick | + | [17] Rudenick P.A., Bordone M., Bijnens B.H., Soudah E. et al. ''A multi-method approach towards understanding the pathophysiology of aortic dissections—the complementary role of in-silico, in-vitro and in-vivo information''. In: Statistical atlases and computational models of the heart. Berlin, pp 114–123, 2010. |
| − | [18] Thomas T. Tsai, | + | [18] Thomas T. Tsai, M.D., Marty S. Schicht, M.S., Khalil Khanafer, PhD, Joseph L. Bull, PhD, Ramon Berguer, MD, PhD and Kim A. Eagle, MD. ''Tear size and location impacts false lumen pressure in an ex vivo model of chronic type B aòrtic dissection'', 2007. |
| − | [19] Y.C.Fung. ''Mechanical properties of living tissues''. Biomechanics, Springer, 1993. | + | [19] Y.C. Fung. ''Mechanical properties of living tissues''. Biomechanics, Springer, 1993. |
| − | [20] M. Catanho, M.Sinha, V.Vijayan. ''Model of Aortic Blood Flow Using the Windkessel Effect''. 2012. | + | [20] M. Catanho, M. Sinha, V. Vijayan. ''Model of Aortic Blood Flow Using the Windkessel Effect''. 2012. |
| − | [21] L. F. Shampine | + | [21] L.F. Shampine and M.W. Reichelt. ''The Matlab ODE Suite'', SIAM J. Sci. Comput., 18, 1–22, 1997. |
| − | [22] E Soudah, | + | [22] E. Soudah, E.Y.K. Ng, T.H. Loong, et al. ''CFD Modelling of Abdominal Aortic Aneurysm on Hemodynamic Loads using a Realistic Geometry with CT''. Computational Mathematical Methods in Medicine, 2013:472564, 2013. |
| − | [23] Soudah | + | [23] Soudah E., Rossi R., Idelsohn S. and Oñate E. A reduced-order model based on the coupled 1D-3D finite element simulations for an efficient analysis of hemodynamics problems. ''Computational Mechanics'', 54(4), 1013-1022, 2014. |
| − | [24] Keynes | + | [24] Keynes G. ''The Life of William Harvey''. Oxford, Clarendon Press, 1978. |
| − | [25] Shim | + | [25] Shim E.B., Sah J.Y. and Youn, C.H. ''Mathematical modeling of cardiovascular system dynamics using a lumped parameter method. Japanese Journal of Physiology'', 54, 545-553, 2004. |
| − | [26] J. Calvo Plaza. ''Simulación del flujo sanguíneo y su interacción con la pared arterial mediante modelos de elementos finitos.'' Tesis Doctoral | + | [26] J. Calvo Plaza. ''Simulación del flujo sanguíneo y su interacción con la pared arterial mediante modelos de elementos finitos.'' Tesis Doctoral, 2006. |
| − | [27] Burattini | + | [27] Burattini R. and Natalucci S. ''Complex and frequency-dependent compliance of viscoelastic windkes'' '''sel''' '' resolves contradictions in elastic windkessel''. Medical Engineering and Physics, 20, 502-514, 1998. |
| − | [28] Baumann | + | [28] Baumann E.D. ''Praxagoras de Kos.'' Janus 41, 167-185, 1937. |
| − | [29] O.Lewis | + | [29] O. Lewis. ''Praxagoras on Cos on arteries, pulse and pneuma: fragments and interpretation''. 2017. |
| − | [30] Soudah | + | [30] Soudah E. Computational fluid dynamics indicators to improve cardiovascular pathologies. Thesis Doctoral, UPC, 2016. |
Latest revision as of 14:53, 18 March 2020
Resumen
Mediante la interconexión de elementos eléctricos tales como una resistencia, un inductor y un condensador se ha desarrollado un modelo de orden reducido del sistema arterial capaz de describir el comportamiento del flujo sanguíneo. En dicho modelado están representados implícitamente las diferentes ecuaciones diferenciales que describen el comportamiento de este sistema. Esto permite obtener y regular rápidamente, la actuación del modelo conjunto, tanto en condiciones fisiológicas normales como ante situaciones patológicas, lo que lo convierte en una herramienta útil para la docencia o investigación en fisiología cardiovascular.
Se implementaron dos modelos arteriales diferentes, un modelo elástico y un modelo visco elástico, con el propósito de analizar el flujo y la presión sanguínea que se podrían producir ante diferentes condiciones fisiológicas. Con el objetivo de analizar ambos modelos, se contrastó usando diferentes órdenes de elasticidad, se estudió la patología de disección aórtica y se comparó los resultados de manera cualitativa con soluciones similares observadas en la literatura. Para poder realizar dichas simulaciones se implementó un código de resolución de ecuaciones diferenciales ordinarias (DAE) en Matlab.
Abstract
Through the interconnection of electrical elements such as a resistor, inductor and capacitor, has been developed a reduced-order model of the arterial system capable of describing the behaviour of blood flow. In this modelling, the different differential equations that describe the behaviour of this system are represented implicitly. This allows us to obtain quickly and regulate the performance of the joint model, both in normal physiological conditions and in pathological situations, which makes it a useful tool for teaching or research in cardiovascular physiology.
It was implemented two different arterial models, an elastic model and a viscoelastic model, with the aim of analysing the flow and blood pressure that could occur under different physiological conditions. In order to analyse both models, it was contrasted using different orders of elasticity, the pathology of aortic dissection was studied and the results were compared qualitatively with similar solutions observed in the literature. In order to perform these simulations, it was implemented in Matlab a code for solving ordinary differential equations (DAE).
Agradecimientos
Quería agradecer a mi tutor Eduardo Soudah, por darme toda la ayuda posible a su abasto cuando lo he precisado y por guiarme para coger las riendas del trabajo.
En especial a mis padres, por su infinita paciencia y su apoyo incondicional en cualquier situación imaginable.
Glosario
| E | Módulo de Young | [Pa] |
| h | Espesor del vaso | [m] |
| L | Longitud del vaso | [m] |
| pin | Presión de entrada | [mmHg] o [Pa] |
| pout | Presión de salida | [mmHg] o [Pa] |
| qin | Flujo de entrada | [m3/s] |
| qout | Flujo de salida | [m3/s] |
| r | radio interno del vaso | [m] |
| µ | Viscosidad de la sangre | [Pa·s] |
| η | Viscosidad de un material | [Pa·s] |
| ρ | Densidad de la sangre | [Kg/m3] |
| Deformación | - | |
| σ | Tensión | [Pa] |
| R | Resistencia | [Pa·s·m-3] |
| L | Inductor | [Kg·m-4] |
| C | Condensador | [m3·Pa-1] |
| Diferencial de flujo en función del tiempo | [m3/s]/[t] | |
| Diferencial de presión en función del tiempo | [mmHg] o [Pa] /[t] | |
| M | Matriz utilizada de 1’s y 0’s | - |
| CV | Coeficiente de variación | [%] |
| σ* | Desviación típica | - |
| Media de muestras | - |
1. Prefacio
1.1. Iniciativa
El gran interés mostrado por el funcionamiento y el comportamiento del sistema cardiovascular y, además, el poder recrear el comportamiento fisiológico de éste mediante la simulación, fueron los principales motivos para el desarrollo de este trabajo. También, sumado al hecho de poder poner en práctica los conocimientos adquiridos en Matlab durante el grado de ingeniería biomédica.
1.2. Requisitos previos
El conocimiento y uso del programa Matlab era de vital importancia, puesto que el trabajo se realiza con él en su totalidad. Por ello, era necesario contar con un sólido conocimiento del lenguaje de programación de éste para poder hacer un buen uso de esta herramienta. A parte, también era importante tener un conocimiento previo de conceptos eléctricos y de hemodinámica sanguínea para recrear los modelos en RLC y sus respectivas ecuaciones de presión y flujo. Por último, y no menos importante, tener una base matemática sobre ecuaciones diferenciales ordinarias y de cómo resolverlas, ayuda en este caso, a la determinación y resolución de éstas mediante métodos numéricos.
2. Introducción
El presente trabajo está dentro del campo de la biomecánica1. El objetivo de esta rama de la ciencia es utilizar el conocimiento de las leyes mecánicas, herramientas y formulación matemática para elaborar modelos lo más realistas posibles del comportamiento de estructuras biológicas. Por ejemplo, el estudio del flujo sanguíneo, análisis de órganos, etc. La primera característica de la biomecánica es que es una ciencia multidisciplinar que involucran a la biología y mecánica. En este caso, la colaboración entre ambas disciplinas consiste en que la biología aporte el estudio de los fenómenos vitales, y la mecánica proporcione la teoría, los modelos matemáticos y los métodos de solución. Estos modelos matemáticos permiten hacer la simulación y a partir de éstas, se pueden hacer predicciones sobre el estado futuro de los elementos de estudio.
A su vez, dentro de la biomecánica, se encuentra la hemodinámica, la rama que tiene por objetivo estudiar el flujo sanguíneo. Este estudio no se focaliza sólo en el movimiento de la sangre, como obtener el caudal, flujo y presión, sino que también en las fuerzas que genera dicho flujo sobre los elementos sobre los que interactúa, como los vasos sanguíneos o el corazón. Sin embargo, este trabajo se centrará en el análisis y evaluación de los primeros.
(1) Según la Real Academia Española (RAE), es la ciencia que estudia la aplicación de la mecánica en las estructuras y órganos de los seres vivos.
2.1. Motivación
Hoy en día las enfermedades cardiovasculares representan la principal causa de muerte entre los países desarrollados y contribuye a casi el 30% de todas las enfermedades mundiales mortales según la Organización Mundial de la Salud (OMS). Esas patologías están estrictamente relacionadas con las condiciones de la circulación sanguínea, por lo tanto, una compresión de la hemodinámica local puede tener aplicaciones útiles para la investigación médica.
No obstante, la extrapolación directa de estos parámetros hemodinámicos es complicada, pues la circulación de la sangre está dentro del cuerpo vivo, por lo que debe haber un compromiso entre la precisión de las mediciones y su nivel de invasividad al determinarlas [30].
La necesidad de seguir investigando acerca de estos sistemas debido a la trascendencia e impacto en la salud mundial que tienen, hace que se realicen estudios y descubrimientos de manera continuada con el fin de mejorar los tratamientos ya existentes, descubrir factores de relevancia y prevenir el efecto de diferentes hábitos o costumbres en la fisiología de este sistema tan importante. Es en este marco donde se sitúa este trabajo, en servir de utilidad recreando mediante una simulación numérica el flujo sanguíneo en una situación característica, pero aplicable a otras circunstancias [16,22,23].
Este hecho permite una interpretación sencilla y rápida, mediante la analogía a un sistema eléctrico menos complejo –al tratarse de un sistema de orden reducido-, de lo que está sucediendo y anticipándose al comportamiento de una red arterial en concreto en una situación específica.
2.2. Objetivo del trabajo
El propósito de este trabajo es desarrollar una herramienta numérica basada en modelos de orden reducido (0-D) para resolver modelos matemáticos que describan la presión y el flujo sanguíneos. Estos modelos deben son capaces de predecir las características hemodinámicas dentro del sistema arterial ante diferentes situaciones fisiopatológicas. La sangre se simula como un fluido homogéneo, incompresible y newtoniano2, mientras que las arterias serán como tubos cilíndricos, rectos y deformables. El comportamiento arterial se representará mediante pequeños circuitos eléctricos compuestos por una resistencia, un inductor y un condensador (RLC).
Estos modelos se aplicarán, primeramente, sobre una sección de la aorta, simulando el primer flujo de entrada, y después se ampliará hacia el tronco aórtico, modelando una patología denominada disección aórtica. Se representará esta patología sobre un modelo elástico y visco elástico, donde se colocará una resistencia extra en serie con el condensador para simular la propiedad de viscoelasticidad del vaso.
Para poder realizar la simulación, se utilizará el programa Matlab, con el que se creará un código computacional en el que se introducirán los datos fisiológicos de la sección arterial con la que se va a trabajar, y mediante un sistema matricial de ecuaciones diferenciales, que se resolverán, se obtendrán los parámetros requeridos que son las ondas de flujo y presión sanguíneas de cada uno de estos modelos y se compararan. También se someterá al modelo visco elástico a una evaluación cuantitativa, aumentando y disminuyendo los valores de la elasticidad para ver el comportamiento de la presión sanguínea. Finalmente se contrastarán cualitativamente ambos modelos y con soluciones similares observadas en la literatura.
(2) Un fluido newtoniano es aquel cuya viscosidad puede considerarse constante. Este hecho hace que sea más sencillo describir su comportamiento.
2.3. Estado del arte
La irrupción de la aplicación de las matemáticas para representar fenómenos físicos supuso un cambio de perspectiva, pasando de descripciones y explicaciones cualitativas del sistema cardiovascular a una cuantificación del comportamiento de éste mediante ecuaciones matemáticas. A continuación, se da una visión histórica breve de esta evolución.
Pinceladas históricas
Partiendo del siglo IV a.C. Aristóteles describió la comunicación del corazón con los vasos sanguíneos, aunque no identificó todavía la circulación la circulación sanguínea. Siguiendo al siglo III a.C. Praxágoras, distinguió las funciones de las arterias y las venas, observando que las arterias impulsaban sangre y las venas no [28,29]. A finales del siglo II, el griego Galeno propuso que se propagaban los pulsos de presión originados en el corazón a través de la red arterial [24].
Durante un período más avanzado, alrededor del siglo XIII, Ibn Al-Nafi fue el primer médico que describió correctamente la circulación pulmonar [24]. Antes de eso, la teoría común y popular del flujo sanguíneo era que la comida se convertía en sangre en el hígado y luego funcionaba como un combustible.
Más tarde, tocando el siglo XVII, el inglés William Harvey, mediante unos estudios donde midió el caudal de la sangre que pasa por las venas, concluyó que la sangre bombea desde el corazón y por el cuerpo en sentido unidireccional [27].
A mediados del siglo XVIII, Malpighi y Van Leeuwenhoek describieron la existencia de capilares que unían venas y arterias, demostrando definitivamente que el sistema circulatorio era cerrado y el flujo unidireccional.
Durante el mismo siglo, Daniel Bernoulli investigó las leyes que rigen la presión arterial y relacionó la presión sanguínea con la velocidad de la sangre en la siguiente ecuación:
|
|
(1) |
donde V es la velocidad del fluido en la sección considerada, es la densidad del fluido –tomando como un flujo incomprensible, por lo que este valor es constante-, P es presión del fluido, tomando z como la diferencia de altura desde una cota de referencia y g como la gravedad. Además, esta ecuación era aplicable en flujos laminares con un caudal constante y viscosidad nula.
En el siglo XIX, el francés Jean Lonard Marie Poiseuille estableció la ley que lleva su nombre, dónde relaciona la ley física que explicaba la relación de la caída de presión y el flujo sanguíneo en condiciones de flujo estacionario. La ecuación rige del siguiente modo:
|
|
(2) |
donde es el caudal, la diferencia de presiones, el radio del tubo, la longitud del tubo y la viscosidad del fluido.
A lo largo del siglo XX, Otto Frank estableció el modelo “Efecto Windkessel”, donde la aorta se concibe como un tubo elástico con capacidad de almacenar fluido [25]. Así, en el extremo del corazón el fluido es introducido de forma intermitente, mientras que en otro extremo el fluido sale de forma aproximadamente constante. Fue entonces cuando, el sistema circulatorio fue concebido como un embalse elástico dónde el corazón bombea sangre y desde el cual sale una red de conductos no elásticos para abastecer el cuerpo.
Se elaboraron modelos matemáticos que simularon esta teoría y más tarde, Noordagraaf y Westerhof [25], utilizaron el concepto de Windkessel y construyeron un modelo analógico eléctrico de las principales arterias de la circulación sistémica y lo aplicaron para paredes de tubos elásticos. En su estudio, las principales arterias de la circulación sistémica se dividieron en un numero finito de segmentos arteriales. Cada segmento se representa por un circuito eléctrico, compuesto por una resistencia, un inductor y un condensador.
Hoy en día, el flujo sanguíneo puede ser modelado con diferentes niveles de precisión, que incluyen: modelos de orden reducido (0-D), modelos unidimensionales (1-D) [22], y modelos tridimensionales (3-D) [23]. La principal diferencia entre los modelos de orden reducido y los unidimensionales y tridimensionales es que los primeros, no tienen dependencia espacial, y solo dependen del factor tiempo.
Los modelos 0-D vienen definidos por una ecuación diferencial ordinaria, ya que es una función de una sola variable –el tiempo-Por el contrario, los otros modelos incluyen dimensiones espaciales, en el caso del 1-D una dimensión espacial, y en el caso del 3-D, tres dimensiones espaciales, x, y y/o z, dentro de un sistema de coordenadas elegido.
No obstante, para el presente trabajo, se ha escogido desarrollar el modelo en un sistema de orden reducido, 0-D.
Con el fin de entender mejor el estudio de la mecánica vascular, se brinda a continuación, una breve descripción del sistema y del funcionamiento del mismo y algunos aspectos más generales de la mecánica del corazón, el sistema vascular e insistiendo en el sistema arterial, pues será el sistema en el que se trabaja.
2.4. El sistema circulatorio
El sistema circulatorio se trata fundamentalmente de un elemento de transporte que facilita el desplazamiento de diferentes substancias a través del flujo sanguíneo mediante una bomba muscular –el corazón- en un circuito cerrado de tubos elásticos – vasos sanguíneos-.
De esta manera, el flujo sanguíneo presenta un papel crucial dentro del sistema circulatorio (SC) tanto en el transporte y distribución de nutrientes, oxígeno y agua al organismo, ajuste de la temperatura corporal, como en la eliminación de subproductos metabólicos (CO2 y agua) de los tejidos corporales.
Existen dos tipos de circulación que sigue el flujo, que se corresponden con dos trayectorias distintas a través de dos sistemas de vasos sanguíneos independientes:
- a. La circulación sistémica, que es la que parte del corazón (concretamente del ventrículo izquierdo) con sangre oxigenada y limpia, y a través de las arterias, arteriolas y capilares, llega a todos los tejidos para realizar el suministro. Después regresa por las venas hasta el corazón, entrando en éste por la aurícula derecha.
- b. La circulación pulmonar, que se encarga de eliminar los gases de desecho, como el dióxido de carbono (CO2) y tomar nuevo oxígeno. Parte del ventrículo derecho del corazón y lleva la sangre empobrecida en oxigeno hacia los pulmones, donde se realiza el cambio de gases. Posteriormente la sangre ya enriquecida con dicho oxígeno, vuelve al corazón entrando por la aurícula izquierda.
La trayectoria de la circulación sistémica es más larga y presenta más ramificaciones respecto a la pulmonar. Por ello, las presiones necesarias para cada una de ella son diferentes, siendo mayores en la sistémica.
| Figura 1. Circuito de circulación arterial (rojo) y circulación venosa (azul) en el cuerpo humano Fuente: https://accessmedicina.mhmedical.com/content.aspx?bookid=1858§ionid=134366226 |
2.4.1. El corazón
El corazón es el órgano muscular del sistema circulatorio que actúa como doble bomba que impulsa la sangre a lo largo de las dos circulaciones pulmonar y sistémica. Para mantener estos dos circuitos separados, el corazón se divide en dos partes -derecha e izquierda-, cada una de ellas con dos cámaras conocidas como aurículas y ventrículos: ventrículo izquierdo (LV), ventrículo derecho (RV), aurícula izquierda (LA) y aurícula derecha (RA) (véase Figura 2). El bombeo de la sangre se proporciona a través de dos fases que se alternan en cada latido, una fase de contracción –dónde se produce la eyección de la sangre-, llamada sístole, con una fase de relajación, llamada diástole. La repetición continua de estas dos fases representa el ciclo cardíaco (véase Figura 3). Durante la sístole, la sangre se bombea hacia la aorta y durante la diástole, la válvula mitral se abre, y la sangre fluye hacia la cavidad ventricular desde la aurícula, para ser impulsada nuevamente.
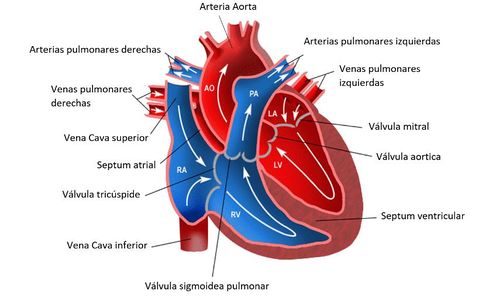
|
| Figura 2. Recorrido del flujo sanguíneo a través del corazón Fuente: http://miaulaenlared.blogspot.com/2018/01/6-primaria-el-corazon-y-el-recorrido-de.html |
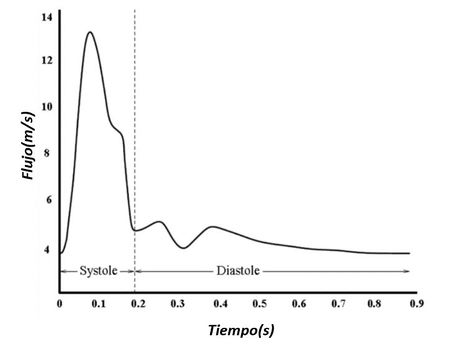
|
| Figura 3. Fase sístole y diástole durante un ciclo cardíaco Fuente: D.Corridini. A numerical tool for the simulation of the blood flow, 2014 |
La duración media común del ciclo cardíaco es de aproximadamente 0.80 segundos, que equivale a unos 70 latidos por minuto. El caudal en condiciones normales puede ser de 4,9 litros/minuto, aunque en situaciones de máximo esfuerzo puede llegar a 35 litros/minuto. El valor del caudal en reposo de 4900 ml/minuto se ha calculado suponiendo 70 latidos/minuto y un volumen de bombeado de 70 ml. Entonces se obtiene 70·70=4900 ml/min.
2.4.2. El sistema vascular
Los vasos sanguíneos que componen el sistema vascular (SV) son las arterias, las venas y los capilares, los cuales se diferencian por su tamaño, el tejido que los compone y el diámetro del conducto. Las arterias-que forman el sistema arterial (SA)-, son las de mayor diámetro, son vasos elásticos fuertes, capaces de transportar la sangre a grandes presiones. Inician el circuito llevando la sangre oxigenada desde el corazón al resto de los órganos.
Las funciones principales del SA dentro del SV son, primeramente, preservar una presión sanguínea adecuada. Como el corazón es una bomba intermitente, el avance de la sangre que se produciría sería únicamente en la fase de eyección o fase sistólica. Sin embargo, la estructura elástica de la pared arterial, permite almacenar parte de la energía cinética proporcionada durante la contracción del ventrículo, como energía potencial que actúa expandiendo la pared. Así, posteriormente, durante la diástole, la pared vuelve a su estado de reposo, transmitiendo energía cinética de la sangre acumulada en su interior. Debido a estos cambios de presión, el SA actúa como un amortiguador pulsátil, pues las oscilaciones generadas por estas variaciones de presión y flujo son atenuadas según la sangre avanza por la red arterial hacia el corazón. Esta disminución de las fluctuaciones es realizada principalmente por arterias menores y arteriolas. Esto asegura continuidad tanto de la presión periférica arterial como del flujo sanguíneo a nivel capilar. Del mismo modo, es capaz de regular la distribución del flujo sanguíneo. Esta función recae básicamente en los las arteriolas o vasos de resistencia3. La pared arteriolar presenta un mayor contenido de fibras musculares y, por lo tanto, es el vaso principal que puede modificar su diámetro ampliamente y controlar así el flujo que llega a un determinado segmento vascular. Este cambio diametral de las arteriolas –vasoconstricción4 y vasodilatación5- está regulado a través de factores nerviosos y hormonales, atendiendo siempre, a las necesidades del organismo.
|
| Figura 4. Diagrama simplificado del sistema vascular. Las secciones en rojo pertenecen al sistema arterial (sangre oxigenada) y las secciones en azul al sistema venoso (sangre desoxigenada) Fuente: https://es.wikibooks.org/wiki/Anatom%C3%ADa/Aparato_Circulatorio |
No obstante, la pared arterial no es homogénea. Consta de tres capas concéntricas, que de dentro a fuera se conocen como: la túnica íntima o interna –capa interna-, constituida por endotelio y está presente en arterias y venas. La túnica media –capa media-, compuesta por fibras musculares lisas y fibras de colágeno, y la túnica externa o adventicia –capa externa-, formada por tejido conectivo laxo, compuesta por fibroblastos y colágeno.
Además, está el lumen, que es el espacio interior de la arteria, por donde fluye la sangre.
También se encuentran diferencias entre la composición de cada capa en los distintos vasos, encontrando arterias elásticas que conforman las grandes arterías como la aorta, la arteria pulmonar o la carótida y suelen presentar un gran diámetro que puede variar de 1 cm a 2.5 cm. Presentan una gran área del lumen, y son conocidos como vasos de baja resistencia.
| Figura 5. Partes de la arteria en comparación con la vena Fuente: https://periodicosalud.com/diferencias-arterias-venas/ |
Las arterias elásticas tienen una gran cantidad de filamentos de colágeno y elastina en la túnica media, que ayudan a mover y almacenar el flujo de sangre durante la sístole y a mantener una presión relativamente constante a su paso.
Las arterias musculares cuya función básica es distribuir la sangre a los diferentes órganos del cuerpo. Su diámetro oscila entre 1 cm y 0.2 cm. Tienen una gran cantidad de fibras musculares lisas en la túnica media que ayudan a regular el flujo sanguíneo.
Y finalmente las arteriolas. Las arteriolas tienen un diámetro del lumen pequeño respecto a las mencionadas con anterioridad que varía entre 10 μm a 0.2 mm y juegan un papel fundamental en el mantenimiento y la regulación de la presión arterial mediante la contracción variable del músculo liso de sus paredes y la regulación del aporte sanguíneo a los capilares.
Después, el flujo fluye por las arterias y llega a las arteriolas y es dirigido a los capilares, una red de vasos de diámetro muy pequeño, donde se lleva a cabo un intercambio de nutrientes hacia los tejidos. Los capilares unen las arteriolas y las pequeñas ramificaciones procedentes de las venas, las vénulas.
Finalmente, la sangre se recoge en el sistema venoso, el que los vasos se fusionan rápidamente en vasos de mayor tamaño que recogen la sangre de los tejidos y órganos y la llevan de vuelta al corazón. El volumen total del sistema venoso es mucho mayor que el del sistema arterial, aunque las amplitudes de presión y velocidades de flujo son menores respecto a las arterias.
Cada segmento del sistema vascular tiene una combinación ideal de tamaño, composición de pared, espesor y área para trabajar adecuadamente en cada circunstancia. Por ejemplo, la aorta y las arterias de mayor tamaño tienen una pared con un mayor contenido de colágeno y elastina debido que su principal función es la de enviar sangre a alta presión a todas las regiones del cuerpo que abastece. Gracias a ello, pueden deformarse y recuperar su tamaño original después de la eliminación de la carga. Véase en la Tabla 1, como la elasticidad de las principales arterias y venas en función de su tamaño y sección.
| Vaso | Diámetro
(mm) |
Espesor de la pared
(mm) |
Modulo Young
(kPa) |
Velocidad
(cm/s) |
Volumen
(cm3) |
Presión
(mmHg) |
| Arteria Aorta | 25 | 2 | 12.5 | 48 | 100 | 120 |
| Arterias mayores | 1-15 | 1 | 12 | 45 | 100-300 | 100-40 |
| Arteriolas | 0.01-0.5 | 0.03 | 7 | 5 | 40-50 | 50 |
| Capilares | 0.006-0.01 | 0.001 | 3 | 0.1 | 200-250 | 30-12 |
| Vénulas | 0.01-0.5 | 0.003 | 1.5 | 0.2 | 280-300 | 12-10 |
| Venas | 0.5-15 | 0.5 | 1 | 10 | 200-700 | 10-5 |
| Vena Cava | 30 | 1.5 | 0.5 | 38 | 300 | 2 |
Cabe añadir que, como se ha mencionado en párrafos anteriores, en términos fisiológicos, el comportamiento de las paredes de los vasos sanguíneos presenta una propiedad elástica llamada viscoelasticidad. Dicha propiedad, proporciona el denominado “mecanismo de almacenamiento de energía”, como un resorte comprimido o un condensador eléctrico para almacenar la energía de la sangre durante la sístole (Figura 5).
La propiedad viscosa disipa la energía transmitida a las paredes del vaso durante el latido. En la diástole, la sangre almacenada se empuja hacia la parte inferior de la red arterial y como resultado, se produce un flujo sanguíneo suave y pulsátil a través el sistema circulatorio.
Estas características de comportamiento se tendrán en cuenta para la realización de este trabajo, pues se determinarán flujos y presiones, por una parte, con variables elásticas y por otra, visco elásticas.
(3) Se conoce como resistencia vascular a la dificultad que opone un vaso sanguíneo al paso de la sangre a su través. Si la resistencia vascular disminuye, el flujo aumenta, por el contrario, si la resistencia vascular aumenta, el flujo disminuye
(4) Disminución del diámetro de un vaso por contracción de las fibras musculares.
(5) Aumento del diámetro de un vaso por la relajación de las fibras musculares.
2.4.3. La sangre
La sangre es un tejido líquido encargado de suministrar sustancias necesarias como nutrientes y oxígeno a las células que forman los tejidos y de recoger los desechos metabólicos de cada uno. Está formada por partículas en suspensión conocidas los glóbulos rojos, los glóbulos blancos y las plaquetas (45% del volumen total, y una parte líquida llamada plasma que representa el otro 55% restante y está compuesto mayoritariamente de agua).
Los glóbulos rojos que componen la sangre, también conocidos como eritrocitos, son los responsables del intercambio de oxígeno y dióxido de carbono en las células. Por otro lado, los glóbulos o leucocitos, juegan un papel importante en el sistema inmunológico humano, pues activan la respuesta inmunitaria del organismo, interviniendo en su defensa contra sustancias extrañas o agentes infecciosos. Las plaquetas o trombocitos, principales responsables de la coagulación sanguínea.
El plasma a su vez, es una solución electrolítica diluida que contiene varias proteínas y diferentes sustancias disueltas. También transporta nutrientes, azucares, hormonas y substancias de desecho contenidos en la sangre. Al contener una gran cantidad de agua, y al ser ésta incomprensible, da las propiedades de incompresibilidad a la sangre.
| Figura 7. Composición de la sangre |
Desde un punto de vista mecánico, la sangre está compuesta por glóbulos rojos flexibles suspendidos en el plasma, que hacen que se comporte como un fluido no newtoniano debido a la heterogeneidad de su composición. Por tanto, cualquier modelo constitutivo que se proponga ha de reflejar como mínimo estas dos características, viscosidad e incomprensibilidad. No obstante, para el desarrollo de este trabajo, se toma la sangre como fluido newtoniano con una viscosidad propuesta de valor constante.
2.4.4. Ondas de presión y flujo
La presión sanguínea es el elemento que se ejecutara durante este trabajo. El parámetro de presión es la fuerza por unidad de superficie que ejerce la sangre contra las paredes vasculares, que viene determinada por el volumen de sangre que contiene el SA y por las propiedades de las paredes, midiéndose normalmente en mmHg, dina/cm2 o Pascales. Por otro lado, el flujo o caudal es el volumen de sangre por unidad de tiempo que atraviesa el vaso, que se puede expresar en ml/s o l/min.
El corazón envía sangre de un modo pulsátil a las arterias. En cada sístole entra un volumen de sangre en la aorta provocando un incremento de presión, dando lugar a su punto máximo, conocido como presión sistólica. Del mismo modo, durante cada diástole, la presión disminuye representando su punto mínimo, presión diastólica. Estos cambios cíclicos generan una onda de presión también llamada pulso arterial.
En esta onda, hay una sección ascendente que se desarrolla durante la sístole ventricular, y una fase descendente, que se inicia con una breve disminución de presión, volviendo a aumentar y generando una muesca que presenta el nombre de incisura dicrota, producto del cierre de la válvula aortica. –la válvula aórtica se cierra cuando la presión en la aorta supera a la ventricular-. La presión arterial media es un parámetro cardiovascular importante ya que proporciona el valor de presión con que la sangre llega a los tejidos.
La diferencia entre la presión arterial sistólica y la diastólica se denomina presión diferencial o presión de pulso.
| Figura 8. Curva de presión durante la sístole y la diástole |
Las formas de la onda de presión y su velocidad dependen tanto del rendimiento del corazón como de las características de la red vascular. La Figura 9 muestra cómo la presión disminuye a medida que se aumenta la distancia respecto al corazón.
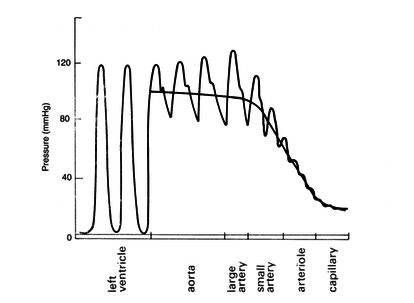
|
| Figura 9. Presión pulsátil en el árbol vascular Fuente: D.Corridini. A numerical tool for the simulation of the blood flow, 2014 |
Durante el período de diástole, la presión en el ventrículo izquierdo es cercana a cero y la válvula aórtica se mantiene cerrada a causa de la diferencia de presión de aproximadamente unos 80 mmHg. En la aorta, la presión arterial media es aproximadamente de unos 100 mmHg con una presión sistólica de 120 mmHg y una presión diastólica de 80 mmHg. En las arteriolas la presión disminuye considerablemente y tanto la presión diastólica como la sistólica convergen gradualmente. Cuando llega el flujo sanguíneo al sistema de capilares, el flujo es aproximadamente constante y más lento, lo que facilidad el intercambio mediante difusión, de nutrientes y productos de desecho entre la sangre y el tejido enervado.
Observación: Para un adulto joven y sano los valores aceptables de presión sistólica y diastólica oscilan entre 120 mmHg y 80 mmHg respectivamente. No obstante, factores constitucionales (sexo, raza, peso) y del estilo de vida (dieta, hábitos como el consumo de tabaco o alcohol, etc.) influyen de forma muy importante en la presión arterial haciendo variar los valores y la forma de la onda.
3. Modelo matemático
En el capítulo anterior se proporcionó un conocimiento básico preliminar sobre el sistema cardiovascular. A lo largo de este capítulo veremos los modelos y las ecuaciones matemáticas utilizadas que describen el flujo y la presión sanguínea mediante un modelo elástico lineal y otro visco elástico [12]. Los modelos matemáticos permiten, no solo estudiar la propagación de las ondas en un segmento arterial aislado, sino también el sistema de circulación global, o al menos, aproximar su comportamiento.
3.1. Modelos de orden reducido 0-D
El modelado en 3D del flujo sanguíneo en el sistema cardiovascular puede proporcionar simulaciones muy detalladas, pero las derivaciones e implementaciones y la complejidad de dicho sistema lo hacen computacionalmente muy costoso y complejo.
Sin embargo, es posible derivarlo a modelos más simples, sencillos y menos costosos utilizando modelos de orden reducido, 0-D.
Estos modelos describen la física del sistema muy simple y el cambio de parámetros da una idea del comportamiento del sistema implementado. Se pueden encontrar diferentes modelos según los parámetros utilizados y si trabajan en un solo bloque –modelo unicompartimentado- o que se trabajan en varios bloques – modelo policompartimentado-.
3.1.1. Modelo unicompartimentado
En un modelo unicompartimentado, la red arterial o venosa de todo el sistema se representa con un solo circuito, compuesto de una resistencia, una inductancia y/o un condensador. Este tipo de modelo se empezó a utilizar para modelar la circulación del cuerpo entero, –un bloque para la circulación arterial, otro bloque para la circulación pulmonar, etc.- pero estaba limitado puesto que no puede describir los cambios de presión y de caudal en ubicaciones específicas de la red arterial (Figura 10).
| Figura 10. Modelo esquemático tipo unicompartimentado simulando la circulación en cada sistema. Cada mini-modelo equivale a un sistema específico |
3.1.2. Modelo policompartimentado
En los modelos policompartimentados, por el contrario, la red arterial se divide en múltiples segmentos; cada arteria, como en el caso de este trabajo, está representada por un circuito eléctrico RLC (Figura 11).
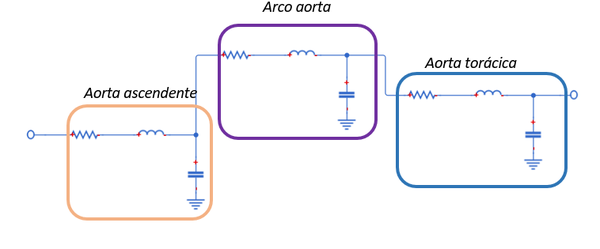
|
| Figura 11. Modelo esquemático tipo policompartimentado. Cada mini-modelo equivale a un vaso |
Los valores de estos parámetros se calculan a partir de las propiedades de los vasos sanguíneos –módulo de Young, diámetro del vaso, longitud del vaso, grosor, viscosidad del fluido, entre otros.
Con el fin de construir una red de vasos llenos, los circuitos eléctricos de cada segmento se conectan entre sí utilizando las condiciones adecuadas de salida y de bifurcación. Las condiciones de bifurcación se derivan de leyes de conservación de masa y del momento. Por eso, antes de construir la red, es fundamental conocer y considerar las características de cada segmento, es decir, su comportamiento mecánico, condiciones de bifurcación de flujo, etc.
Por lo tanto, los modelos que contienen parámetros agrupados en bloques poli-compartimentados, se consideran más adecuados para simular, estudiar y analizar el comportamiento general del sistema cardiovascular. Este tipo de modelo será el que se empleará en este trabajo.
3.2. Modelo matemático en 0-D
El modelado matemático es una herramienta útil y eficiente para la predicción e investigación de enfermedades cardiovasculares. El objetivo básico de estos modelos es una mejor compresión del comportamiento sistema cardiovascular de una manera rápida y no invasiva.
Las variables de estado hemodinámico están representadas por un numero finito de variables, definidas por segmentos vasculares específicos. Aunque dicho modelo tiene baja resolución espacial, es útil para evaluar el rendimiento general del sistema o subsistemas cardiovasculares, como las arterias del brazo, la bifurcación de la carótida, entre otros.
Por lo tanto, un segmente del vaso sanguíneo se puede representar por un circuito eléctrico, combinando una resistencia, un inductor y un condensador. Existe una analogía entre el flujo en un tubo y el flujo de corriente en un circuito eléctrico. El potencial eléctrico o voltaje (V) corresponde a la diferencia de presión de conducción (Δp) en el segmento determinado del vaso, la corriente (A) es análoga al flujo sanguíneo (q), la resistencia (R) es la representación de la resistencia del flujo viscoso, el capacitor es análogo a la complianza del tubo (C), el inductor es la inercia de la sangre (L) y la impedancia corresponde a la resistencia terminal de los vasos terminales (Rb). (Véase tabla 2)
Dichos parámetros se pueden calcular usando ecuaciones matemáticas-sistema de ecuaciones diferenciales ordinarias acopladas que describen la variación en el tiempo- que dependen de las propiedades físicas y dimensiones de dichos vasos arteriales para la determinación de parámetros como presión y flujo.
| SISTEMA VASCULAR | SISTEMA ELÉCTRICO |
| Presión (p) (mmHg) | Voltage (V) |
| Flujo (q) (m3/s) | Corriente (A) |
| Resistencia de la sangre (R) (Pa·s·m-3) | Resistencia (R) (Ω=V/A) |
| Inercia de la sangre (L) (Kg·m-4) | Inductancia (L) (H= V·s/A) |
| Complianza (C) (m3·Pa-1) | Capacitor (C) (F=A·s/V) |
En este apartado, se presenta la formulación matemática de los modelos con sus parámetros correspondientes, pues el trabajo se centrará en la representación de varios segmentos específicos del sistema arterial del cuerpo humano, diferenciándolos en su comportamiento visco elástico y elástico y comparándolos entre ellos (m3·Pa-1).
3.2.1. Modelo equivalente 0-D al segmento vascular
3.2.1.1. Modelo elástico
Los modelos elásticos en estas mismas dimensiones se basan en la idea de que el flujo atraviesa un tubo cilíndrico rígido y recto de longitud establecida l, espesor h y diámetro Ø. Teniendo en cuenta que los parámetros que lo componen simulan el comportamiento elástico de éste, su representación se adhiere a la Figura 12.
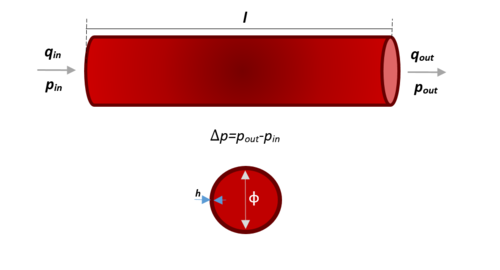
|
| Figura 12. Dimensiones y características de un vaso sanguíneo representado |
El circuito que modula un solo vaso arterial se ve representado por una resistencia, un condensador y una bobina, en el que se podrá calcular la presión que equivale al voltaje que lo atraviesa y el flujo, que equivale al amperaje. El modelo elástico se puede representar en un circuito L-invertido tal que así,
| Figura 13. Circuito equivalente (RLC) de un vaso. Qin y pin representa la corriente y el voltaje del fluido en la entrada del vaso respectivamente. Qout y pout es la corriente y el voltaje de salida del vaso |
Los parámetros a determinar en el circuito se describirán a continuación.
3.2.1.1.1 Parámetros de flujo y presión
- a) Ecuaciones de presión y flujo en segmentos no terminales
Como se ha precisado con anterioridad, mediante la analogía electrica se determinaran los parámetros fisiologicos de presión y flujo. Para ello, se definiran, dentro de cada segmento, dos únicas incognitas que, tras aplicar las leyes de corriente y voltage de Kirchhoff se obtendrá un sistema de dos ecuaciones diferenciales para presión , y flujo .
De esto modo, serán las incógnitas en cada vaso a determinar, y , que se definirán como:
|
(3) | |
|
(4) |
No obstante, en el presente trabajo, la presión de entrada se calcula a partir de un flujo de entrada teórico definido por una senoide, entonces se hace un pequeño cambio en las ecuaciones para que puedan aplicarse en todas las situaciones.
Por un lado, sabiendo que, la ecuación diferencial del cálculo del flujo en la arteria i, donde , se tiene que:
|
|
(5) |
siendo la presión de salida del segmento anterior, la presión, la resistencia, la inductancia y el flujo que se quiere determinar en un segmento indicado.
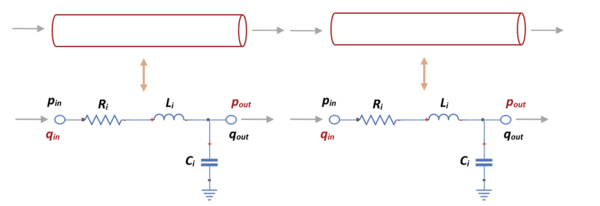
|
| Figura 14. Analogía eléctrica entre dos vasos arteriales y el circuito eléctrico en segmentos no terminales |
Por otro, la ecuación diferencial del cálculo de la presión en la arteria i, donde , se saca:
|
|
(6) |
siendo el flujo calculado en el segmento indicado, el flujo calculado en el segmento siguiente y la complianza en ese segmento.
- b) Ecuaciones de presión y flujo en segmentos terminales
El segmento de red arterial que se utiliza en este trabajo se divide en un número finito de vasos que incluyen arteriolas y capilares.
Debido al gran gasto informático y a la complejidad que esto presenta, se cierra la red arterial mediante una conexión en cascada de dos circuitos elásticos L y L-invertidos.
Como en el caso anterior, aplicando las leyes de Kirchhoff, se obtiene un sistema de primer orden de 3 ecuaciones diferenciales:
|
(7) | |
|
(8) | |
|
(9) |
donde , y son las variables a determinar. En cada segmento terminal, es la presión obtenida en el segmento anterior y mantiene un valor constante de 15 mmHg que representa la presión venosa media que se usa para calcular el flujo de salida en el límite, es la resistencia terminal fija obtenida de la literatura [4].
| Figura 15. Representación esquemática de la analogía eléctrica en un vaso terminal que fluye hacia capilares |
3.2.1.2. Modelo viscoelástico
3.2.1.2.1 Parámetros de flujo y presión
- a) Ecuaciones de presión y flujo en segmentos no terminales
El sistema visco elástico presenta las mismas características que la anterior en segmentos no terminales, es decir, las incógnitas son igualmente, y y se podrán obtener partiendo de las mismas características anatómicas de las arterias, como su longitud, diámetro, espesor, etc. Así pues, el flujo que atraviesa el vaso significativo se podrá calcular con:
|
|
(10) |
siendo igualmente, la presión de salida del segmento anterior, la presión, la resistencia, la inductancia y el flujo requerido.
No obstante, antes de definir la ecuación de la presión, es importante conocer la mecánica del comportamiento del vaso, puesto que al contrario que antes, no es solamente elástico, sino que presenta un comportamiento visco elástico en su naturaleza dentro del S.C. Esta característica de la pared puede ser representada mediante el modelo de Voigt [12].
La representación mecánica de este modelo se interpreta mediante un amortiguador (η) y un muelle ( ) que sigue la ley de Hooke6 conectado en paralelo al amortiguador, que representa un sólido que sufre una deformación viscoplástica reversible. Bajo la aplicación de una tensión constante, el material se deforma a un ritmo progresivamente lento. Una vez se le retira esa tensión exterior, el material se relaja hasta su estado no deformado original.
Se define matemáticamente por una ecuación que relaciona el comportamiento elástico y viscoso del material:
|
|
(11) |
donde es la tensión a la que está sometido el material, E es el módulo de Young, la deformación que se le aplica, la viscosidad del material, y es la derivada en función del tiempo de la tensión.
Con esto, la analogía eléctrica del modelo de Voigt se puede obtener considerando la resistencia R y la capacitancia C en serie [12]. Aplicando la ley de Kirchhoff sobre voltaje y corriente, se tiene:
|
|
(12) |
donde es voltaje, C la capacitancia, la carga, R la resistencia y la corriente eléctrica I.
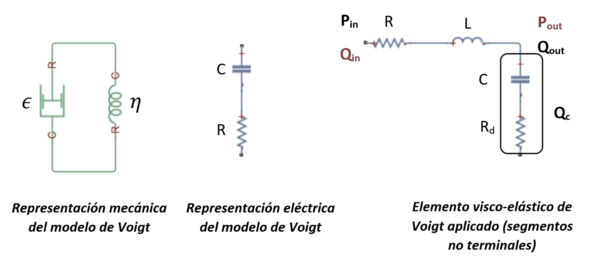
|
| Figura 16. Representación esquemática mecánica y eléctrica equivalente del modelo de Voigt |
En el caso de los vasos arteriales, la relación tensión-deformación o carga-voltaje se puede simplificar en términos de presión-volumen. La ecuación correspondiente explica la naturaleza visco elástica de la pared de los vasos siendo:
|
|
(13) |
donde es la presión, es la complianza del vaso, indica el volumen de sangre, es la resistencia que mide viscosidad del vaso y = es el flujo de sangre que atraviesa el vaso. Sabiendo que la incógnita equivale a out , tomando la derivada de (ec.13) se obtiene,
|
|
(14) |
donde se debe cumplir que,
|
|
(15) | |
|
|
(16) |
y substituyendo en (ec.10), (ec.15) y (ec.16) en la (ec.14) para el cálculo de la presión en segmentos no terminales, finalmente obtenemos que,
|
|
(17) |
que queda para la formula general,
|
|
(18) |
Hay que tener en cuenta que es la resistencia que determina la viscosidad en particular que cada vaso específico, no es fija. Por lo tanto, cada segmento tendrá la suya propia, establecida por [12].
Así pues, la analogía eléctrica que representa el vaso no terminal y el sistema viscoelástico presenta la siguiente forma (Figura 17).
| Figura 17. Analogía eléctrica simplificada entre un vaso sanguíneo y su sistema viscoelástico |
- b) Ecuaciones de presión y flujo en segmentos terminales
En el caso visco elástico, en los segmentos terminales también se cierra la red arterial mediante una conexión en cascada de dos circuitos L y L invertidos.
Aplicando pues, las leyes de Kirchhoff, se obtienen un total de 3 ecuaciones diferenciales de primer orden,
|
(19a) |
|
(19b) |
|
|
(20) |
como ecuación de presión.
| Figura 18. Representación esquemática de la analogía eléctrica en un vaso terminal viscoelástico que fluye hacia capilares |
La analogía eléctrica que representa el vaso no terminal y el sistema visco elástico presenta la siguiente forma.
Una vez habiendo tenido claro la estructura del circuito, se definen los parámetros eléctricos que lo componen, tales como el resistor R, la inductancia L, y el condensador C.
3.2.1.3. Parámetros eléctricos
3.2.1.3.1 Resistencia del flujo sanguíneo (R)
El parámetro R representa la fuerza de resistencia a la que el fluido está sometido a medida que avanza por el vaso de determinadas características, tales como el diámetro interno del vaso (d), su longitud (l), entre otros. Un parámetro importante a tener en cuenta en la R es la viscosidad del fluido, puesto que está presente cuando el fluido es estable u oscilatorio, disipando la energía de éste, aunque el flujo este acelerando o desacelerando. La viscosidad sanguínea que en este caso toma un valor constante de µ=0.004 Pa·s.
La resistencia total del flujo en un segmento concreto se modela mediante resistores y puede calcularse a partir de la ecuación de Poiseuille (ec.2), que como vimos en apartados anteriores, describe la relación entre la caída de presión, Δp y el flujo sanguíneo constante y q a través de un vaso sanguíneo uniforme y rígido.
Presenta la siguiente ecuación:
|
|
donde aislamos R
|
|
(21) |
donde es la longitud del vaso, la viscosidad sanguínea y , el radio interno del vaso. La ecuación presente también es conocida como la ley hidrodinámica de Ohm. Generalmente, R se obtiene de la ley de Poiseuille, pero en la práctica esta expresión se denomina ley hidrodinámica de Ohm. Las unidades que se usará con el resistor será en Pa·s·m-3.
3.2.1.3.2 Complianza del vaso sanguíneo (C)
Cuando el flujo atraviesa un vaso elástico, el volumen del vaso puede variar. La clave del efecto de capacitancia sobre el flujo en un vaso elástico es que afecta al volumen total del vaso, por lo tanto, la velocidad de flujo en la entrada puede no ser la misma que en la salida debido a la variación de presión. Así pues, la capacidad de la pared de un vaso sanguíneo para expandirse y contraerse con los cambios de presión se conoce como capacitancia o complianza del vaso, C. La relación entre presión-volumen se puede cuantificar de dos modos. Por una parte, con la capacitancia C y por otra, con la elasticidad, es decir, el módulo de la elasticidad, .
La capacitancia se calcula usando la siguiente ecuación, donde es el cambio de volumen de sangre, y la variación de presión en el segmento, quedando como:
|
|
(22) |
donde añadimos las propiedades de los vasos sanguíneos siendo el módulo de Young y el grosor de la pared del vaso, tal que:
|
|
(23) |
Las unidades que se usarán con el condensador serán en m3·Pa-1.
3.2.1.3.3 Inercia de la sangre (L)
En cada latido del corazón, el fluido se acelera y se desacelera en el tiempo de un modo no inmediato debido a su inercia, L.
Dicho parámetro relaciona la caída de presión : con el cambio de caudal en un segmento, que se expresa mediante: .
Del mismo modo, el valor numérico de L, se puede obtener utilizando las propiedades de los vasos sanguíneos, aplicando la ley de Newton relativa al movimiento que implica, fuerza (F), masa (m) y aceleración donde = y siendo =m .
Partiendo de ahí, se aplica a un vaso de longitud, :
|
(24) |
donde es el área de sección transversal del vaso cilíndrico, kg/m3 es la densidad de la sangre y V es el volumen del fluido que atraviesa ese segmento. Aplicando la definición de flujo volumétrico , donde es la velocidad en ese tramo, se deriva y se obtiene:
|
|
(25) |
aislamos el diferencial
|
|
(26) |
Así, substituyendo y en la ecuación tal que,
|
|
(27) |
que como se ha mencionado, L es la relación entre y el caudal, quedando finalmente como:
|
|
(28) |
Las unidades utilizadas con el inductor serán en Kg·m-4.
3.2.1.4. Condiciones del modelo
3.2.1.4.1 Condiciones de bifurcación
La descomposición de segmentos vasculares requiere tener en cuenta la relación entre varios de ellos dentro de una misma red arterial, es decir, la bifurcación de vasos. Por ello, se definen también condiciones de bifurcación tanto para las presiones como para los flujos, quedando la estructura y las ecuaciones algebraicas tal que:
|
(29) | |
|
(30) | |
|
|
(31) |
en presiones tanto de fusión como divergencia del vaso.
| Figura 19. Representación esquemática de bifurcación de la red arterial |
Estas ecuaciones se obtienen de la conservación de la masa y del momento, que se traduce en que, la presión siempre será constante y el caudal del flujo debe conservarse en una bifurcación.
Los flujos divergentes se dan a cabo durante la bifurcación de los vasos sanguíneos. De acuerdo a la conservación de masa mencionada, el flujo del nodo 1 sería igual a la suma del flujo del nodo 2 y el nodo 3 (), siendo la presión constante en todo el segmento, es decir, la presión de salida en el nodo 1 ha de ser igual a la de entrada del nodo 2 y 3. Del mismo modo ocurre con la conservación de masa en zonas donde el flujo se fusiona, el flujo del nodo 3 ha de ser la suma del flujo del nodo 1 y 2 () y, de acuerdo con la ley de conservación del momento, para este caso la presión total también permanece continua en todos los nodos.
3.2.1.4.2 Condiciones de salida
La longitud total de los vasos sanguíneos en el sistema cardiovascular humano de una persona adulta es aproximadamente de unos 95.000 kilómetros. Con estas cifras, es prácticamente imposible modelar decenas de miles de capilares de arteriolas y capilares del sistema circulatorio.
Por eso, una solución viable existente es la de agrupar todos los nodos posteriores que componen el sistema arterial, en segmentos terminales. Los capilares son considerados vasos de resistencia, de modo que se usa una resistencia terminal Rb para presentar el efecto acumulativo de la microcirculación más allá de los segmentos terminales. Este resistor será constante y presentará un valor de 1.89E+09 Pa·s·m-3[4].
Además, se aplica una condición de contorno de presión constante, pout, conocida como condición de frontera de Dirichlet7, para la resolución de las ecuaciones diferenciales. Entonces, el valor de pout –que se trata de la presión venosa media para calcular el flujo de salida en el límite pout -será de 15 mmHg (2000 Pa) [12]. Este valor, junto con el circuito terminal, se usó igualmente para los cálculos de las ecuaciones diferenciales, aunque el segmento no fuese realmente terminal en el cuerpo humano.
3.2.1.5. Resolución numérica
Para que se pueda resolver el modelo matemático hay que tener en cuenta que el número total de ecuaciones ha de corresponder al número total de variables desconocidas puesto que ha de ser un sistema determinado. Tanto el modelo elástico como el visco elástico, hay dos ecuaciones diferenciales por cada segmento arterial representado no terminal: aorta torácica, lágrima proximal, lágrima distal, el FL y el TL, haciendo un total de 8 ecuaciones diferenciales. Juntamente con el segmento terminal, que añade otra ecuación diferencial más referente a la aorta torácica.
Además, como para cada bifurcación se deben cumplir las leyes de cantidad y momento y conservación de masa, se añaden al sistema 4 ecuaciones algebraicas más, haciendo un total de 13 ecuaciones.
Debido a que este sistema contiene tanto ecuaciones diferenciales como ordinarias, se obtiene un sistema de ecuaciones algebraicas diferenciales (DAE). Hay que remarcar que, tanto el modelo elástico como el visco elástico, tienen el mismo número de ecuaciones diferenciales y algebraicas, pero con la diferencia, que como se mencionó en el Apartado 3.2.1.2, la presión arterial en la salida de cada segmento para el modelo elástico, solo depende de la resistencia terminal, pero para el modelo viscoso, depende de la complianza del vaso (C) y de la resistencia de la arteria.
El número total de incógnitas será de 13 (presión y caudal de entrada y de salida en cada segmento no terminal, y caudal de entrada, de salida y presión para el segmento terminal), pero debido a que se conoce el caudal en la entrada del sistema en la aorta ascendente –se explicará en apartados siguientes-se obtiene un sistema de 12 ecuaciones con 12 incógnitas.
Para poder resolver este sistema de ecuaciones algebraicas diferenciales se necesita definir una matriz de masa. Esta matriz de masa tiene que ser diagonal constante con 1 para las variables diferenciales y 0 para las variables algebraicas, representándose: , con definida.
Por ejemplo, un sistema DAE con 2 ecuaciones diferenciales y una variable algebraica se expresaría como:
Por lo tanto, para el modelo desarrollado, la matriz de masa será de [12x8], de los cuales 1 son los primeros 8 elementos de la diagonal que serán igual a 1 y el resto igual a 0 correspondiendo a las ecuaciones algebraicas. Una vez definido la matriz de masa y las ecuaciones diferenciales y algebraicas, se utiliza el método de diferenciación numérica – ode15s – implementado en Matlab [21].
Destacar que este método es muy eficiente para sistemas en los que existen variación en la solución, como el presente. Es decir, el caudal de entrada posee zonas en las que el flujo varía lentamente(diástole) y zonas donde el flujo varía rápidamente (sístole). El modelo también se implementó mediante el lenguaje de programación Matlab.
(6) La ley de Hooke establece que el alargamiento unitario que experimenta un material elástico es directamente proporcional a la fuerza que se le aplica. La forma más común de representarla es mediante un muelle, donde se relaciona la fuerza F ejercida por el muelle con la elongación δ provocada por la fuerza aplicada, quedando F=-k δ, donde k es la constante elástica del muelle.
(7) La condición de frontera de Dirichlet se emplea cuando en una ecuación diferencial ordinaria o en una derivada parcial, se le especifican los valores de la solución que necesita la frontera del dominio
4. Resolución de los modelos
En esta sección se aplica la herramienta numérica explicada en apartados anteriores, a un modelo experimental. Primeramente, se modificará levemente la elasticidad del modelo visco elástico para ver el comportamiento de la presión, se relacionará cualitativamente este modelo con una versión experimental, y finalmente se compararán cualitativamente y cuantitativamente los modelos visco elástico y elástico.
Los datos que se utilizan en este caso son clínicamente relevantes, pues las resistencias periféricas, los condensadores y las inductancias y las propiedades geométricas son calculadas a partir de datos reales [9] y, por lo tanto, tienen valores fisiológicos realistas. Se han considerado los siguientes casos significativos:
- Sección aorta en sistema elástico
- Disección aórtica en sistema elástico
- Disección aórtica en sistema visco elástico
4.1. Modelo elástico de la arteria aorta
4.1.1. Parámetros de entrada
Se exponen a continuación, las condiciones de entrada al sistema para poder llevar a cabo la simulación, como será la recreación del primer flujo y presión de entrada.
Como primera validación del modelo utilizado se ha de asumir que:
- El ciclo cardiaco empieza en sístole.
- El período de sístole es 2/5 respecto al periodo total del ciclo cardíaco.
- La complianza arterial, la resistencia periférica y la inercia son representadas por un condensador, una resistencia y una bobina respectivamente.
- El flujo inicial que se obtendrá será el calculado en la aorta ascendente.
Con ello, se establecen los datos fisiológicos generales obtenidos en que la densidad de la sangre, ρ, será ρ=1050 y la viscosidad de la sangre µ, será µ=4 mPa·s.
Para la entrada de flujo del primer latido (qi), se impone una función de caudal periódico. Cada período consiste en una onda sinusoidal, para reproducir la fase de la sístole y la fase de la diástole [20].
El flujo de sangre que emite el ventrículo hacia la aorta será representado durante el ciclo cardiaco completo-siendo este de 0.8 s- como I(t) con amplitud durante la sístole, pues durante la diástole, los ventrículos están relajados y no hay flujo emergente, por lo tanto, I(t)=0. Sin embargo, la contracción ventricular durante el primer periodo, la sangre sí que fluye hacia la aorta definiendo la siguiente ecuación:
|
|
(32) |
donde t es tiempo en segundos, es el periodo de ciclo completo en segundos, es el período de sístole en segundos, y representa el vector divido entre . El parámetro se ha determina como 2/5 de acuerdo a los parámetros dinámicos del ciclo cardiaco. Se establece también, un flujo entrante en el primer latido de 70 cm3.
Usando ésta información obtenemos la constante en:
|
|
(33) | |
|
|
(34) |
| Gráfica 1. Primer latido simulado del flujo en la entrada de la arteria aorta |
Usando el software MATLAB y el código desarrollado, se obtiene que en el bombeo de inyección durante la sístole. Ese será el vector inicial utilizado, qi.
Una vez se obtiene el vector de entrada, se debe obtener la presión primera para poner iniciar. Se representa a continuación una pequeña simulación de la presión inicial con la que se emprende el circuito obtenida a partir del flujo de entrada. Se obtienen un total de 20 ciclos cardiacos, de 0,8 segundos cada uno.
| Gráfica 2. Primer parámetro de presión simulado en la entrada de la arteria aorta |
Los valores obtenidos en pin se consideran aceptables pues como se aprecia en la Figura 12, se obtienen valores máximos de ± 120 mmHg como presión sistólica, y valores mínimos de ± 80 mmHg como presión diastólica. Los valores fisiológicos reales utilizados de la aorta ascendente obtenidos de para esta iniciación son:
| Nombre | Longitud (m) | Radio (m) | Espesor (m) | Módulo de Young (Pa) | Pout(Pa) |
| Aorta ascendente | 0.06 | 0.01477 | 0.00143 | 587000 | 2000 |
A partir de estos datos obtenemos los valores eléctricos con las formulas mencionadas en el capítulo tres:
| R, Resistencia (Pa·s·m-3) | L, Inductancia (kg·m-4) | C, Condensador (m3·Pa-1) |
| 1.3088E+04 | 9.1476E+04 | 1.4266E-09 |
4.1.2. Inicio de la aorta
Partiendo del primer latido del apartado anterior, se procederá a la simulación del comportamiento de presión y flujo en el primer segmento aórtico mediante el modelo elástico. Dicha sección, está compuesta por la aorta ascendente, el arco aórtico y la parte superior de la aorta descendente, la aorta torácica, respectivamente. Esto significa que se empleará un mini modelo para cada parte descrita, es decir, uno para la aorta ascendente con sus datos fisiológicos, otro para el arco aórtico, y otro para la aorta torácica.
Aunque anatómicamente sea un segmento curvado, al hacerlo sobre un modelo 0-D, se tomarán como varios cilindros rectos unidos entre sí, sin tener en cuenta los factores geométricos.
Los datos fisiológicos del modelo serán los siguientes:
| Arteria | Longitud (m) | Radio (m) | Espesor (m) | Módulo de Young (Pa) |
| Aorta ascendente | 0.06 | 0.01477 | 0.00143 | 587000 |
| Arco aorta | 0.02 | 0.0144 | 0.00143 | 819000 |
| Arteria torácica | 0.03 | 0.01355 | 0.00144 | 994000 |
| Arteria | Resistencia (Pa·s·m-3) | Inductancia (kg·m-4) | Condensador (m3·Pa-1) |
| Aorta ascendente | 1.3088E+04 | 9.1476E+04 | 1.4266E-09 |
| Arco aorta | 4.7378E+03 | 3.1775E+04 | 3.2039E-10 |
| Arteria torácica | 9.0649E+03 | 5.3831E+04 | 3.2752E-09 |
La analogía eléctrica del primer segmento queda tal como muestra la Figura 20.
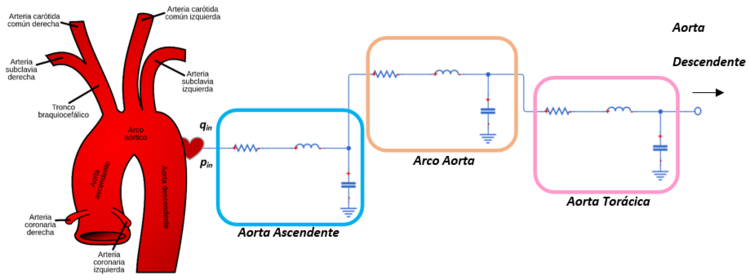
|
| Figura 20. Analogía eléctrica simplificada de la aorta |
Se determina en cada segmento, la presión y el flujo del vaso con los datos fisiológicos expuestos en la página anterior. Cabe destacar que, qin y pin, son los vectores calculados al inicio de la sección y que la presión y el flujo que se calculará en el tercer segmento de la aorta torácica, es el que se empleará para la siguiente sección sobre la disección aórtica.
No obstante, hay que tener en cuenta que, en una persona, esta arteria, solo en los inicios presenta varias bifurcaciones, en la aorta ascendente hay dos, la coronaria derecha y coronaria izquierda, y en arco hay 4, subclavia derecha e izquierda y carótida derecha e izquierda.
Aún y así, para representar este segmento, se ha tomado como un único tubo a representar, el conductor principal, despreciando las bifurcaciones, teniendo en cuenta que la presión sanguínea será la misma.
Lo que se pretende establecer con este modelo, es que, a parte de la funcionalidad del primer latido, la simulación de sección anatómica arterial siguiente sea igual de funcional y recree con la mayor veracidad posible–dentro de lo que los modelos 0-D permiten hacer y representar- las características hemodinámicas de este segmento arterial tan fundamental, como es la aorta.
A continuación, se muestra una gráfica esquemática (Figura 21) [23] de cómo se propaga el flujo (m3/s) a través de la aorta durante la primera sístole, en un período de 0.3 segundos aproximadamente–período de eyección-. Siendo un flujo ínfimo al inicio –unos 4.753E-05 m3/s-, y va aumentando a medida que avanza la primera fase, alcanzando casi los 0.000258 m3/s.
| Figura 21. Representación del flujo aórtico durante la sístole [30] | |||
Tras graficar, se observa como el flujo a través de esta primera sección no varía prácticamente, puesto que el caudal de entrada ha de igual siempre al de salida, es decir, la cantidad de flujo que sale y entra y atraviesa las arterias ha de mantenerse constante, para asegurar un buen funcionamiento de las funciones corporales y asegurar que el riego sanguíneo –en situaciones sin patologías- llegue a todos los extremos sin excepciones.
El pequeño desfase se podría deber a la propagación de onda a través de los tubos. El flujo máximo que se aprecia en la Figura 21, se ve representado en su punto máximo –presión sistólica- en la Gráfica 3.
| Gráfica 3. Curvas de flujo del primer segmento de la aorta, indicando el punto máximo |
Con la presión sanguínea ocurre el mismo fenómeno, debe mantenerse aproximadamente constante a lo largo de todos los vasos arteriales, desde que sale del ventrículo izquierdo, hacia la aorta ascendente, pasando por todo el tronco aórtico y sus ramificaciones hasta los órganos, hasta llegar a las extremidades y los capilares. La propagación de presión sobre todo el sistema arterial durante un latido entero (0.8 segundos aproximadamente) incluyendo sístole y diástole, asumiendo que el latido empieza en sístole, se puede observar simplificado en la Figura 22.
| Figura 22. Propagación de la presión sanguínea durante la sístole [30] | |||
Se puede apreciar como en ambas fases la presión de la sangre se muestra prácticamente constante a través de todo el sistema arterial. En la fase de sístole, el flujo es mayor, con comportamiento creciente, llegando a casi 16500 Pascales (120 mmHg) en los puntos más altos, puesto que es el período de eyección sanguínea y de contracción de los ventrículos (Figura 22). Durante la fase de diástole, donde se produce la dilatación ventricular, la presión sanguínea baja hasta estar entre los 12000 y 10000 Pascales (90-75 mmHg, respectivamente) en los puntos más bajos como las extremidades (Figura 23).
| Figura 23. Propagación sanguínea durante la diástole [30] | |||
En la Gráfica 4, que se anexa a continuación perteneciente a la primera sección de la aorta, se comprueba que la presión de sangre no varía prácticamente en ninguno de los tres puntos. El desfase presente puede deber a la propagación de la onda de presión a lo largo del tubo.
| Gráfica 4. Presión en los primeros segmentos de la aorta |
(8) Hay que añadir que los valores representados en esta figura, son representativos. Son valores medios obtenidos con datos fisiológicos específicos. La cantidad de caudal de una persona puede variar en función de sus características y su actividad física en algún momento determinado. Lo mismo se aplica a los valores de presión.
4.2. Disección aórtica
4.2.1. Patología
Hoy en día, las patologías aorticas representa un subgrupo muy importante dentro de las enfermedades cardiovasculares y, aunque su prevalencia es limitada, se asocian con una mortalidad muy alta (>50%) [12]. A pesar de las técnicas de diagnóstico actuales y las terapias mejoradas, el manejo y el seguimiento de las disecciones aorticas continúan siendo un desafío en la práctica clínica. La disección aórtica clásica empieza con la formación de una pequeña incisión llamada lágrima –tear- en la capa íntima de la arteria, que expone a la capa media siguiente a la presión pulsátil del flujo sanguíneo (Figura 24). Esto conlleva a una escisión en dirección longitudinal de ésta capa media a lo largo de la pared aórtica causando la disección. Este proceso de disección se extiende impulsado por la fuerza hacia delante del flujo sanguíneo aórtico.
Por ello, el lumen quedará dividido en dos partes, el canal principal con el verdadero lumen, TL, y el canal falso, fruto de esta patología, FL. En la mayoría de los casos, el TL y el FL se comunican a través del sitio de entrada y de salida. –véase anatomía de una artería en el Apartado 2.4.2.
| Figura 24. Disección de la aorta ascendente (izquierda). Imagen de la aorta descendente en una resonancia magnética (centro) y en tomografía (derecha). TL: verdadero lumen. FL: Falso lumen Fuente: Validation of numerical flow simulations against in vitro phantom measurements in different type B aortic dissection scenarios, 2013 |
Los pacientes que lo padecen presentan una alta mortalidad a medio/largo plazo, debido a la dilatación progresiva del tejido de la aorta y su posterior ruptura. En la práctica actual, la predicción del resultado se basa principalmente en la determinación del diámetro aórtico máximo.
Sin embargo, se ha visto que este parámetro no es un determinante confiable en la progresión y en la ruptura de la aorta, pues variables hemodinámicas como la presión, las condiciones de flujo, la elasticidad de la pared y factores geométricos como la forma de curvatura de la aorta, la sección de comunicación entre falso lumen y verdadero lumen y el tamaño de las lágrimas juegan un papel importante e influyen directamente en el progreso de dilatación del tejido [17].
Dentro de esta patología podemos encontrar dos clasificaciones en función de la extensión en la aorta ascendente:
- Tipo A: Se origina en la aorta ascendente y se puede extender hacia todo el tronco de la aorta o se detiene en el arco aórtico.
- Tipo B: Se origina en la aorta descendente y rara vez se extiende. No involucra la sección ascendente.
| Figura 25. Tipos de disección aórtica Fuente:https://es.wikipedia.org/wiki/Disecci%C3%B3n_a%C3%B3rtica |
Así pues, el objetivo será la elaboración de un circuito eléctrico en dimensión 0-D análogo a la estructura arterial para simular el comportamiento del flujo sanguíneo dentro de una disección aórtica. Los datos utilizados para recrear las dimensiones de la arteria y sus extremos son propuestos por Alastruey [4].
Se recreará un escenario de tres secciones principalmente, donde se hará hincapié en la sección central perteneciente a la disección aórtica. La simulación se iniciará en la aorta torácica, seguida de una parte aorta descendente donde se hará la disección aórtica, y se finalizará con la aorta abdominal.
Dentro de la disección aórtica, se distinguirá el verdadero lumen (TL) y el falso lumen (FL) alternando diferentes tamaños de las lágrimas simulando hipotéticas situaciones. En cada escenario se determinará la presión en el TL y el FL en la sección proximal y distal tanto en el modelo elástico como en el visco elástico para ver la diferencia del comportamiento de la onda entre ambas y se contrastará desde un punto de vista fisiológico con otros modelos consultados en la literatura [9].
Cada lágrima se representará mediante un resistor con un valor particular. La sección de la aorta abdominal, al ser nuestro segmento terminal se recreará con el modelo de ecuaciones de flujo y presión para segmentos terminales explicados en el capítulo tres.
Los datos fisiológicos de la arteria abdominal y torácica serán los mismos para los tres escenarios y los dos modelos. Presentan los siguientes valores:
| Arteria | Longitud (m) | Radio (m) | Espesor (m) | Módulo de Young(Pa) |
| Arteria torácica | 0.03 | 0.01355 | 0.00144 | 994000 |
| Arteria abdominal | 0.06 | 0.00102 | 0.00127 | 1823000 |
| Arteria | Resistencia (Pa·s·m-3) | Inductancia (Kg·m-4) | Complianza (m3·Pa-1) | Rd (Pa·s·m-3) |
| Arteria torácica | 9.0649E+03 | 5.3831E+04 | 3.2752E-09 | 4.44E+07 |
| Arteria abdominal | 5.64611E+04 | 1.8999E+05 | 1.7279E-10 | 4.17E+06 |
El modelo a representar se localiza y se presenta de la siguiente manera (Figura 26).
| Figura 26. Analogía virtual en 3D de la disección aórtica del modelo representado |
Así pues, los escenarios trabajados serán,
- 1. Escenario primero

|
| Figura 27. Representación de la arteria. Primer escenario |
Las condiciones de la segunda situación serán las siguientes: se determinará la presión en el falso y verdadero lumen en la sección proximal y lo mismo para la sección distal. Los diámetros de las lágrimas en este caso serán del mismo tamaño, siendo de 10 mm la primera lágrima y 10 mm la segunda.
Los datos fisiológicos con los que se simula el modelo tanto elástico como visco elástico del primer escenario y de los demás escenarios de [9] presentan los siguientes valores (Tabla 9).
| Segmento | Longitud (m) | Radio (m) | Espesor (m) | Módulo de Young (Pa) | Rd (Pa·s·m-3) |
| Verdadero Lumen | 0.16 | 0.008 | 0.002 | 1070 | 1.69E+07 |
| Falso Lumen | 0.16 | 0.01615 | 0.002 | 2490 | 1.69E+07 |
| Segmento | Resistencia (Pa·s·m-3) | Inductancia (Kg·m-4) | Complianza (m3·Pa-1) |
| Verdadero Lumen | 8.8532E+04 | 7.9345E+05 | 1.2000E-09 |
| Falso Lumen | 5.33056E+03 | 8.3258E-05 | 1.2761E-09 |
| Ø proximal 10 mm | 1.9118E+07 | ||
| Ø distal 10 mm | 1.9118E+07 |
- 2. Escenario segundo
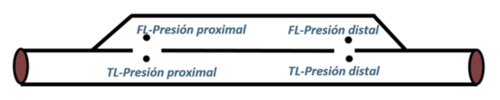
|
| Figura 28. Representación de la arteria. Segundo escenario |
Las condiciones de la segunda situación serán las siguientes; se determinará la presión en el falso y verdadero lumen en la sección proximal y lo mismo para la sección distal. Los diámetros de las lágrimas en este caso serán de 10 mm la primera lágrima y 4 mm la segunda.
Los datos fisiológicos con los que se simula el modelo tanto elástico como visco elástico del escenario segundo presentan los siguientes valores:
| Segmento | Longitud (m) | Radio (m) | Espesor (m) | Módulo de Young (Pa) | Rd (Pa·s·m-3) |
| Verdadero Lumen | 0.16 | 0.008 | 0.002 | 1070 | 1.69E+07 |
| Falso Lumen | 0.16 | 0.01615 | 0.002 | 1510 | 1.69E+07 |
| Segmento | Resistencia (Pa·s·m-3) | Inductancia (Kg·m-4) | Complianza (m3·Pa-1) |
| Verdadero Lumen | 8.8532E+04 | 7.9345E+05 | '1.2000E-09 |
| Falso Lumen | 5.33056E+03 | 8.3258E-05 | 2.1099E-09 |
| Ø proximal 10 mm | 1.9118E+07 | ||
| Ø distal 4 mm | 2.9597E+08 |
- 3. Escenario tercero

|
| Figura 29. Esquema sobre la arteria en el tercer escenario |
Las condiciones de la tercera situación serán las siguientes; se determinará la presión en el falso y verdadero lumen en la sección proximal y lo mismo para la sección distal. Los diámetros de las lágrimas en este caso serán de 4 mm la primera lágrima y 0 mm la segunda, es decir, no habrá segunda lágrima.
Los datos fisiológicos con los que se simula el modelo tanto elástico como visco elástico del escenario primero presentan los siguientes valores:
| Segmento | Longitud (m) | Radio (m) | Espesor (m) | Módulo de Young (Pa) | Rd (Pa·s·m-3) |
| Verdadero Lumen | 0.16 | 0.008 | 0.002 | 1070 | 1.69E+07 |
| Falso Lumen | 0.16 | 0.01615 | 0.002 | 3820 | 1.69E+07 |
| Segmento | Resistencia (Pa·s·m-3) | Inductancia (Kg·m-4) | Complianza (m3·Pa-1) |
| Verdadero Lumen | 8.8532E+04 | 7.93451E+05 | 1.20001E-08 |
| Falso Lumen | 5.33056E+03' | 8.32583E-05 | 1.94695E+08 |
| Ø proximal 4mm | 2.9597E+08 | ||
| Ø distal 0 mm | infinita |
4.2.2. Disección aórtica con modelo elástico
El modelo eléctrico que representará el segmento aórtico patológico se presenta en la Figura 30.
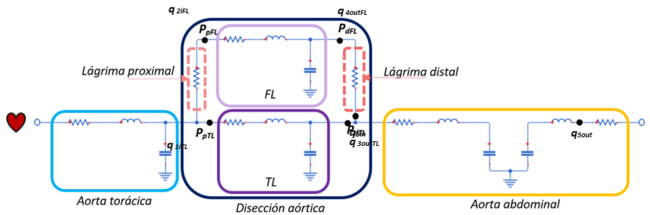
|
| Figura 30. Modelo elástico de la disección aórtica con los parámetros principales a determinar |
Donde las incógnitas principales serán las presiones en las sección proximal y distal tales como PpTL que equivale a la presión proximal del verdadero lumen (TL), PpFL que es la presión proximal a través del falso lumen (FL), PdTL como presión del TL en la sección distal y finalmente, PdFL que representa la presión distal en el FL.
El modelo elástico recrea el comportamiento de los vasos como cilindros, rectos y rígidos. Se divide en cuatro segmentos compuestos por circuitos RLC que pretenden simular una disección aórtica en una sección de la aorta descendente. El primer segmento viene con los valores de qin y pin preestablecidos que se explica en el Apartado 4.1.1.
El modelo que pertenece a esta patología se le añaden dos resistencias en paralelo para imitar el comportamiento de las lágrimas. El cambio de diámetro de las lágrimas se verá reflejado en un cambio en el valor de las resistencias que lo definen –véase apartado anterior-.
La resolución numérica empleada es la mencionada en el Apartado 3.2.1.5, que trata de definir un sistema de ecuaciones diferenciales de primer orden para obtener las variables requeridas. Las ecuaciones que las determinan se presentan de la siguiente manera,
|
|
(35) | |
|
|
(36) | |
|
|
(37) |
La presión restante se calculará mediante la ecuación algebraica,
|
|
(38) |
El parámetro es la resistencia específica para la lágrima en la sección distal. En estas ecuaciones, cada presión viene determinada indirectamente por los valores de flujo calculados en cada segmento (Figura 29).
4.2.3. Disección aórtica con modelo visco elástico
A diferencia del modelo elástico, el modelo visco elástico añade una resistencia extra (Rd) en serie con el condensador para cuantificar la viscoelasticidad del vaso. El modelo eléctrico se representa en el siguiente esquema.
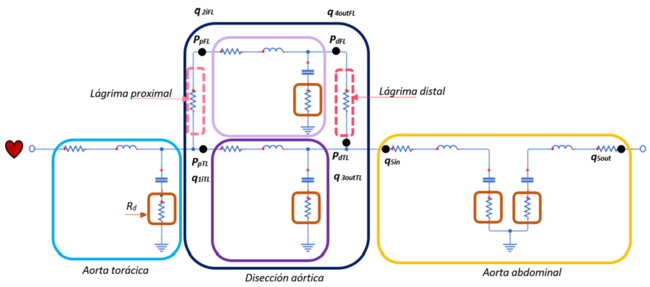
|
| Figura 31. Modelo viscoelástico de la disección aórtica con los parámetros principales a determinar |
De igual modo que en la Figura 30, las incógnitas principales serán las presiones en las sección proximal y distal, PpTL, PpFL que son las presiones proximales a través del verdadero (TL) y falso lumen (FL) respectivamente, PdTL como presión del TL en la sección distal y, PdFL que representa la presión distal en el FL.
El primer segmento también viene con los valores de qin y pin preestablecidos obtenidos del Apartado 4.1.1.
A parte de las dos resistencias que simulan las lágrimas, presenta la resistencia Rd, añadida en serie al condensador, para recrear un modelo de orden reducido con propiedades visco elásticas. La importancia de añadir este resistor extra se encuentra en el hecho de que el comportamiento de la onda de presión que se obtiene, sea más real y que capture algunos comportamientos fisiológicos, como, por ejemplo, la muesca dicrota.
También, al suponer que la pared será más distensible, el pico máximo de la onda será más tardío respecto al elástico. El valor de esta resistencia se obtiene de [12] y varía según la sección, es decir, la aorta torácica tiene una, la abdominal otra, y la parte de aorta descendente en la que se aplica el modelo de la disección aórtica, tanto para el FL como el TL tendrán otra –en este caso se llama Rd as la perteneciente a la de la disección aórtica, y Rd ab, la que se emplea para la aorta abdominal -.
Las ecuaciones, también resultas mediante el método mencionado en el Apartado 3.2.1.5, que rigen la presión especificada en este modelo, se expresan como,
|
|
(39) | |
|
|
(40) | |
|
|
(41) |
y como ecuación algebraica restante aplicando las leyes de Kirchhoff,
|
|
(42) |
El parámetro es la resistencia específica para la lágrima en la sección distal. En estas ecuaciones, cada presión viene determinada indirectamente por los valores de flujo calculados en cada segmento (Figura 30).
4.3. Resultados
Con los modelos mencionados anteriormente, se exponen los resultados obtenidos tras su evaluación en distintas circunstancias. Primeramente, se representa el modelo visco elástico con varias modificaciones del módulo de Young, para ver cómo evoluciona la onda de presión en función del valor de su rigidez. Por otro lado, se someterá a este mismo modelo a una comparación cualitativa con el modelo experimental [9] y finalmente se mostrarán los modelos elástico y visco elástico conjuntamente, para resaltar las diferentes y similitudes, y remarcar la importancia de la variación de la forma de onda que presenta cada modelo. A esta sección se le añadirá una pequeña comparación cualitativa, mediante el cálculo del coeficiente de variación entre ambas ondas.
4.3.1. Variación del módulo de Young del modelo visco elástico
- I. Escenario primero mm, mm)
El valor E de referenia es de 1070 Pascales en el TL. Se ha expuesto el sistema al doble, con 2140 Pascales y a la mitad, 530 Pascales. Para el falso lumen, la E de referencia es de 2490 Pascales, el máximo de 4980 Pascales, y el mínimo de 1250 Pascales, tanto para la sección proximal y distal.
- a. Sección proximal
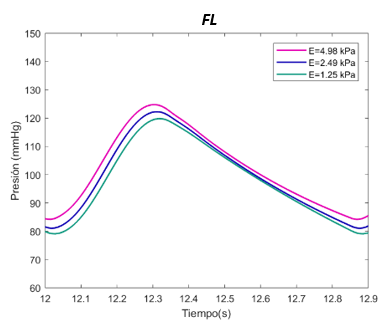
|
| Gráfica 5. Presión en el FL variando el módulo de Young. Sección proximal |
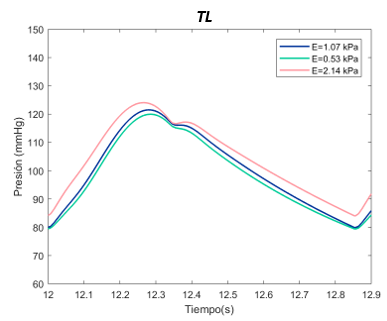
|
| Gráfica 6. Presión en el TL variando el módulo de Young. Sección proximal |
- b. Sección distal
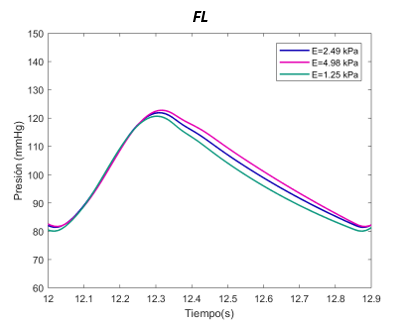
|
| Gráfica 7. Presión en el FL variando el módulo de Young. Sección distal |
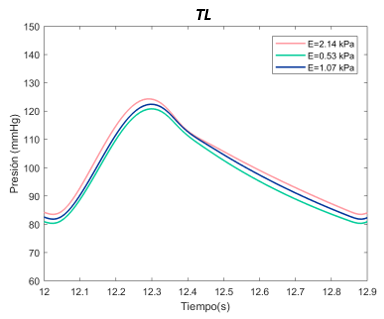
|
| Gráfica 8. Presión en el TL variando el módulo de Young. Sección distal |
- II. Escenario segundo mm, mm)
El valor E de referencia es de 1070 Pascales. Se ha expuesto el sistema al doble, con 2140 Pascales y a la mitad, 530 Pascales, en el caso del verdadero lumen. Para el falso lumen, la E de referencia es de 1510 Pascales, el máximo de 3020 Pascales, y el mínimo de 750 Pascales, para la sección proximal y distal.
- c. Sección proximal
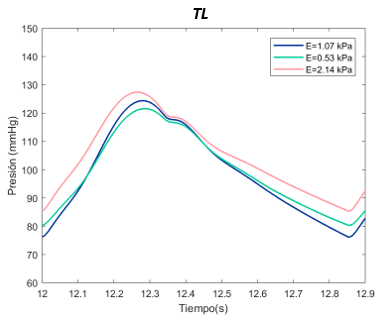
|
| Gráfica 9. Presión en el TL variando el módulo de Young. Seccion distal |
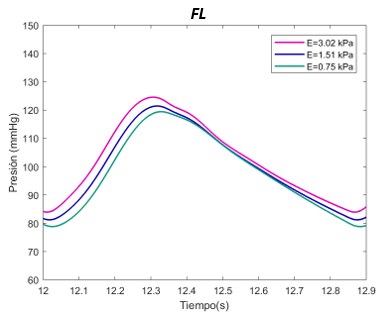
|
| Gráfica 10. Presión en el FL variando el módulo de Young. Seccion distal |
- d. Sección distal
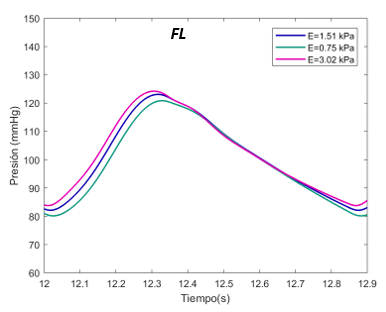
|
| Gráfica 11. Presión en el FL variando el módulo de Young. Sección distal |
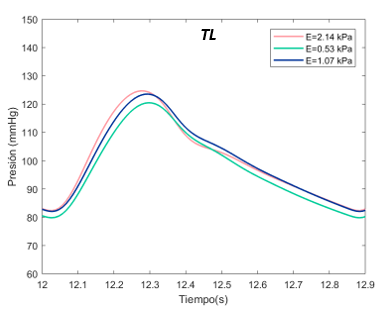
|
| Gráfica 12. Presión en el TL variando el módulo de Young. Sección distal |
- III. Escenario tercero mm, mm)
El valor E de referenia es de 1070 Pascales. Se ha expuesto el sistema al doble, con 2140 Pascales y a la mitad, 530 Pascales, en el caso del verdadero lumen. Para el falso lumen, la E de referencia es de 3910 Pascales, el máximo de 7640 Pascales, y el mínimo de 1910 Pascales, para la sección proximal y distal.
- e. Sección proximal
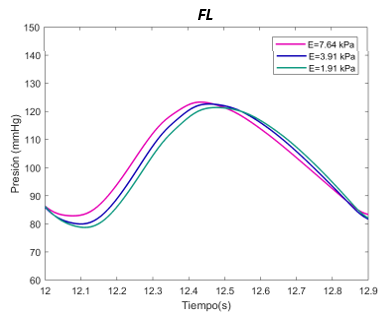
|
| Gráfica 13. Presión en el FL variando el módulo de Young. Sección proximal |
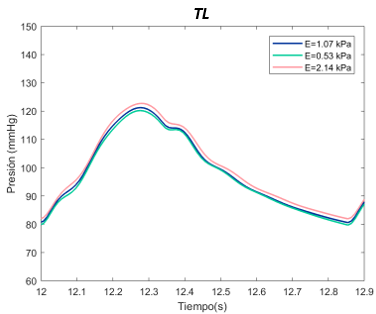
|
| Gráfica 14. Presión en el TL variando el módulo de Young. Sección distal |
- f. Sección distal
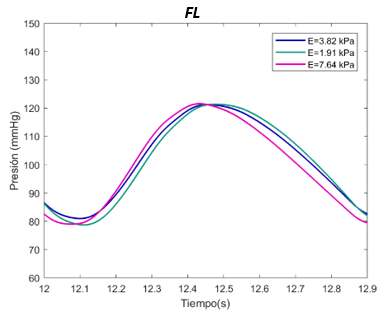
|
| Gráfica 15. Presión en el FL variando el módulo de Young. Sección distal |
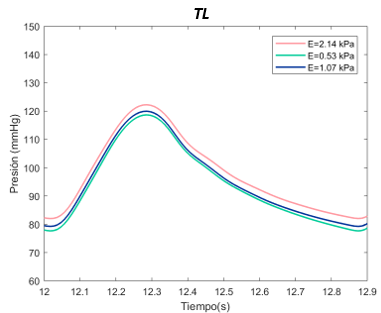
|
| Gráfica 16. Presión en el TL variando el módulo de Young. Sección distal |
El objetivo de alterar el módulo de Young (E) predefinido por otros valores, es la observación del efecto de la elasticidad en la pared arterial en el verdadero y falso lumen y ver las variaciones que se producen en las curvas. Tras observar las gráficas, se puede definir que, un aumento del valor del módulo elástico en el vaso, se traduce a un vaso con mayor rigidez. Este hecho se plasma en un pico de onda más elevado y una presión ligeramente mayor. A la inversa, si E disminuye, el vaso es más deformable y la onda tiene una presión menor.
Esto sucede porque, el comportamiento visco elástico de los vasos proporciona un mecanismo de almacenamiento de energía, que se almacena durante la eyección sanguínea. La energía se disipa por las pareces del vaso. Durante la relajación, la energía almacenada empuja la sangre hacia los vasos siguientes, hecho que provoca un flujo sanguíneo pulsátil, una onda que lo representa más extensa y una ligera disminución en el valor de la presión. La onda que se obtiene en este caso, es más progresiva y con un punto máximo inferior.
Cabe destacar que, la diferencia de la forma de onda entre el TL y el FL se debe al caudal, es decir, el TL presenta un caudal mayor respecto al segundo. Esto puede verse reflejado puesto que en las ondas del TL se aprecian mejor características hemodinámicas destacables, como la muesca dicrota. La onda del FL es más suave y redondeada porque el flujo que lo atraviesa es mucho menor y cuesta percibir alguna característica destacable.
4.3.2. Comparación del modelo visco elástico versus modelo experimental
En esta sección se hará una comparación cualitativa del modelo visco elástico cogiendo como referencia un modelo experimental [9]. El objetivo de este apartado es comparar los cambios relativos de presión que se producen entre el TL y el FL del modelo viscoso desarrollado contra dicho modelo. No se han podido comprobar directamente ambos modelos, puesto que se desconocían ciertos datos del modelo experimental.
El modelo experimental se realizó in vitro –los datos con los que trabajan también son experimentales- sobre un sistema elástico, recreando una disección aórtica con un phantom de látex. Se espera observar similitudes significativas como la propagación de onda, valores parecidos de presiones en el FL y TL y cierta similitud con el comportamiento de la onda, teniendo en cuenta que la comparación se realiza desde un modelo visco elástico y la forma de onda que éste presenta.
Algunos de los datos con los se ha recreado el sistema visco elástico, -módulo de Young para el TL y el FL en cada escenario y las resistencias que representan las lágrimas-fueron recogidas de este modelo experimental. Sin embargo, los parámetros de entrada que se usaron en cada caso eran diferentes, puesto que en el caso del modelo visco elástico del trabajo, qin y pin eran calculadas mediante una senoide, y en el modelo in vitro fueron obtenidas experimentalmente.
- I. Escenario primero ( mm, mm)
- a. Sección proximal
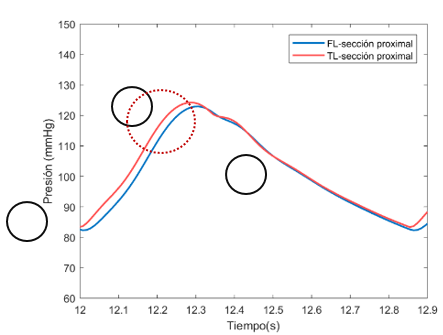
|
| Gráfica 17. Curva de presión en modelo viscoelástico. sección proximal. Primer escenario |
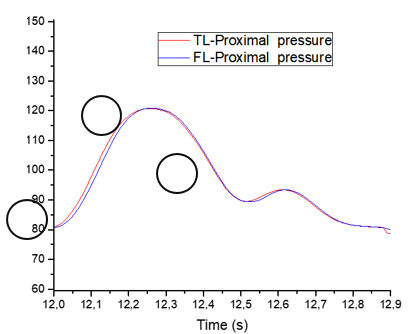
|
| Gráfica 18. Curva de presión en el modelo elástico experimental. sección proximal. Primer escenario |
La evaluación de la primera onda en la parte proximal, muestran claras similitudes. Aunque las ondas son ciertamente diferentes, se puede apreciar como ambas curvas empiezan bajo el mismo comportamiento. Empiezan alrededor de unos 80 mmHg, yendo la presión del TL en cabeza respecto al FL. En el período de crecimiento de onda, ambos casos se separan notablemente, volviéndose a unir en el punto máximo, llegando a la par a unos 120 mmHg.
En la onda visco elástica se muestra el cierre de la válvula aórtica –muesca dicrota-, mientras que, en el modelo elástico experimental, esa característica fisiológica no se representa. Al decrecer la onda, en ambos casos los valores de presión del TL y el FL son muy semejantes y se unifican en una sola línea.
- b. Sección distal
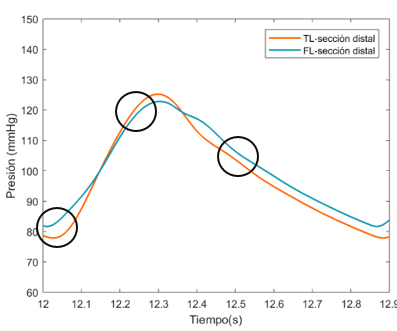
|
| Gráfica 19. Curva de presión en modelo viscoelástico. sección distal. Primer escenario |
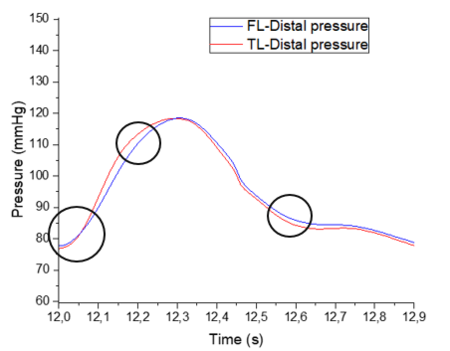
|
| Gráfica 20. Curva de presión en modelo experimental. sección distal. Primer escenario |
En esta sección distal, se aprecia primeramente como la onda de presión del FL de salida es mayor respecto al TL. Durante el crecimiento de la onda, las dos presiones se cruzan, llegando al punto máximo de presión en ambas curvas al mismo instante. –aproximadamente en el segundo 12,3-Durante el período de decrecimiento, la curva del FL se adelanta hasta llegar a su punto más bajo y muestra un área bajo la curva ligeramente más extensa que TL. Cabe decir que respecto el comportamiento general, no se observa apenas desfase de onda entre el FL y TL en ninguno de los dos modelos.
- II. Escenario segundo ( mm, mm)
- c. Sección proximal
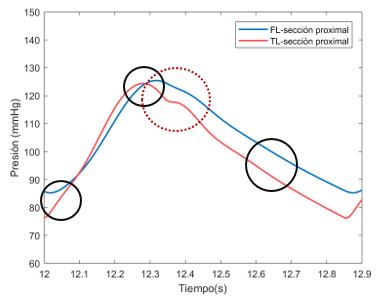
|
| Gráfica 21. Curva de presión en modelo viscoelástico. sección proximal. Segundo escenario |
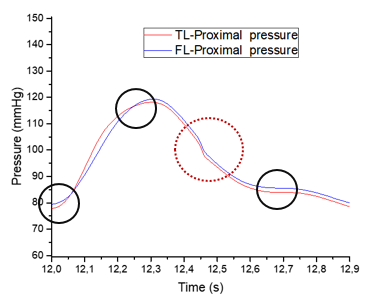
|
| Gráfica 22. Curva de presión en modelo experimental. sección proximal. Segundo escenario |
En el segundo escenario la curva del falso lumen inicia en un valor mayor respecto al verdadero lumen. Inmediatamente se cruzan, siendo el verdadero lumen el que aumenta más rápidamente. Al llegar casi al punto máximo de presión, se vuelven a cruzar intercambiando papeles. El falso lumen alcanza una presión mayor en ambos casos. Se aprecia suavemente un leve salto durante el decrecimiento de las ondas, que pertenece a la incisura dicrota. Se atisba un pequeño desfase de onda en ambos casos, con el falso lumen por delante respecto al verdadero lumen. Durante el decrecimiento perteneciente a la fase de sístole, el TL disminuye más rápidamente.
La variación entre los valores de presión entre el FL y el TL puede deberse simplemente a una cuestión numérica durante la resolución de las ecuaciones diferenciales que componen el sistema. Como se ha especificado en otros apartados, se representan las lágrimas con resistencias. Según el tamaño de la lágrima el valor de dicha resistencia varia. En este caso, como ambas lágrimas poseen diámetros diferentes, la resistencia con la que se trabajará también será diferente, y en este caso, el resistor que representa la lágrima de 10 mm es menor que la de 4 mm, quedando R10 < R4. Por ese motivo, como el cálculo de la presión del falso lumen depende de estas variables indirectamente, puede haber sido un factor que haya hecho que aumente la presión en esa sección.
- d. Sección distal
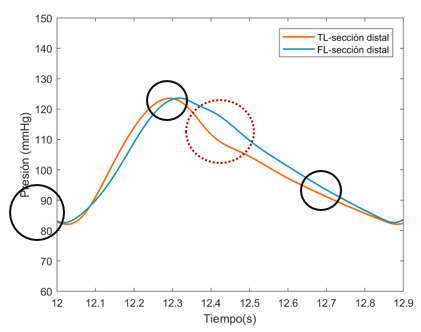
|
| Gráfica 23. Curva de presión en modelo viscoelástico. sección distal. Segundo escenario |
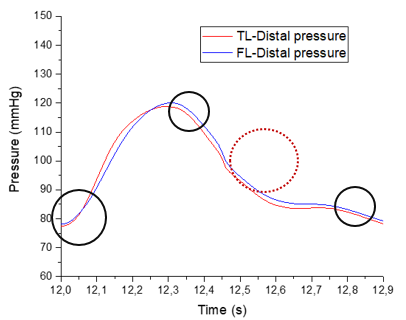
|
| Gráfica 24. Curva de presión en modelo experimental. sección distal. Segundo escenario |
En este caso, las ondas tanto del FL como el TL de cada modelo, salen desde el mismo valor prácticamente, y enseguida cada una toma su camino. La onda del TL crece a mayor velocidad llegando a su punto máximo apenas un poco antes que el FL. Antes de llegar a la presión sistólica, se cruzan y la onda del FL crece brevemente por encima del TL. En el caso viscoso, el FL sigue un comportamiento lineal decreciente, mientras que el TL muestra de un modo muy leve una pequeña protuberancia, indicando la presencia del inciso dicroto. Durante este decrecimiento las curvas se acercan bastante hasta su presión mínima.
La variación entre los valores de presión entre el FL y el VL puede deberse a una cuestión numérica durante la resolución de las ecuaciones diferenciales que componen el sistema, como se ha explicado en el apartado anterior dedicado a la sección proximal.
- III. Escenario tercero mm, mm
- e. Sección proximal
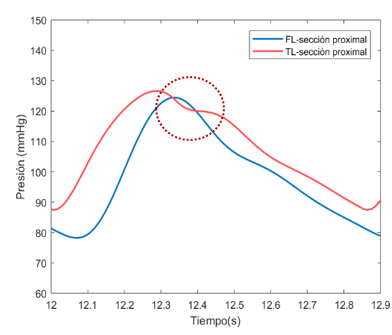
|
| Gráfica 25. Curva de presión en modelo viscoelástico. sección proximal. Tercer escenario |
| Gráfica 26. Curva de presión en modelo experimental. sección proximal. Tercer escenario |
En este último escenario, cabe destacar que la curva del FL no se puede comparar debido a un error en la medida por parte del modelo experimental. Se podría mencionar que el TL del modelo viscoso empieza con una presión superior respecto al falso lumen. También, que en el modelo del trabajo se capta a la perfección la mencionada incisura dicrota, mientras que en el otro no se aprecia apenas, hecho que podría ser una ventaja del modelo viscoso puesto que es capaz de simular con más exactitud características fisiológicas.
No obstante, la curva del modelo viscoelástico muestra unos valores de presión sistólica relativamente altos-superando los 120 mmHg, y de igual modo la presión diastólica -90 mmHg-, en comparación con el otro modelo. Este aumento de los valores, podría deberse a que, la representación de la segunda lágrima de Ø= 0 mm se hizo con una resistencia que tendía a infinito, es decir, una resistencia con un valor tan alto cuya intensidad no pasase a su través.
Se empleó una R de un valor a la orden de E+38. Al emplear un número tan elevado, posiblemente incrementó los valores de las variables en ecuaciones para calcular la presión en el TL.
- f. Sección distal
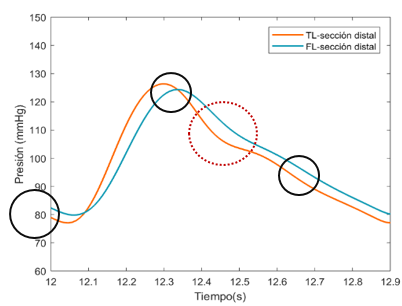
|
| Gráfica 27. Curva de presión en modelo viscoelástico. sección distal. Tercer escenario |
| Gráfica 28. Curva de presión en modelo experimental. sección distal. Tercer escenario |
En la sección distal, las ondas obtenidas en ambos modelos presentan un comportamiento semejante. Se observa al principio como la onda del FL es mayor respecto a la otra. Justo después, se cruzan ambas, siendo la del TL que crece más rápidamente. Ambas muestran una separación considerable, debido al desfase de onda de pulso –FL desfasada hacia delante respecto a TL-.
Tras alcanzar su punto más alto, sobre unos 120 mmHg, donde se vuelven a cruzar, ambas decrecen sin tocarse hasta su presión mínima de unos 80 mmHg. Durante el decrecimiento se puede observar como en los dos modelos se refleja una pequeña ondulación de la onda de presión perteneciente a una leve representación del cierre de la válvula aórtica –justo entre los 12,4 y 12,5 segundos-. Se observa de un modo más pronunciado en el modelo visco elástico.
Cabe destacar que, en todos los casos, los modelos presentaban rangos de presión razonable, siendo aproximadamente 120 mmHg de presión sistólica, y 80-85 mmHg de presión diastólica. El comportamiento genérico se comparte entre ambos, la onda crece, llegando a su máximo de presión, y decrece, llegando a su mínimo.
4.3.3. Comparación modelo del elástico versus visco elástico obtenidos
En este apartado se procederá a realizar un análisis cuantitativo de los modelos visco elástico y elásticos, elaborados en este trabajo, para comparar como afecta la viscoelasticidad del vaso a la forma de onda de presión, equiparando el comportamiento de ambos modelos. Se representarán las presiones pertenecientes del verdadero y falso lumen, tanto de la sección distal, como de la proximal. Los datos fisiológicos de ambos modelos se han recogido de [4,9,12].
Hay recordar que, el modelo elástico utilizado en dimensiones 0-D representa la arteria como un vaso cilíndrico, recto y uniformes, sin tener en cuenta ningún parámetro que registre la distensibilidad del vaso, por lo que se espera que las curvas que se obtengan presenten un comportamiento lineal, sin saltos ni variaciones significativas a lo largo de la curva.
Con diferencia, el modelo visco elástico, incorpora esa resistencia extra en serie con el condensador –explicada en el Apartado 4.2.3- que pretende representar la acumulación de energía de la pared del vaso durante el paso del flujo sanguíneo, intentando mostrar un comportamiento lo más real posible al comportamiento natural del vaso. Con esto, se espera que las ecuaciones que rigen el modelo visco elástico, muestren una curva un poco menos lineal, con algunas variaciones hemodinámicas significativas como la incisura dicrota, la propagación de onda y/o el rebote de la onda, entre otros.
A parte, se realiza también una comparativa cuantitativa, calculando el coeficiente de variación (). Este parámetro estadístico, hace referencia a la relación entre el tamaño de la media y la variabilidad de la variable. El coeficiente de variación se calcula mediante la expresión,
|
(43) |
Esta fórmula presenta la relación entre la desviación estándar de una muestra , y su media , permitiendo así comparar dispersiones de diferentes distribuciones. Generalmente, no dispone de unidades, pero se puede representar en tanto por cien, para tener una idea más clara de lo que se está comparando. Así pues, como más grande sea el valor obtenido por el coeficiente de variación, más dispersión presenta la distribución, que se traduce a una mayor diferencia entre los valores, y a su vez, las ondas. Esta dispersión y la media se calculan,
|
(44) | |
|
(45) |
siendo el número total de muestras.
- I. Escenario primero mm, mm)
4.3.3.1. Presión. Primer escenario
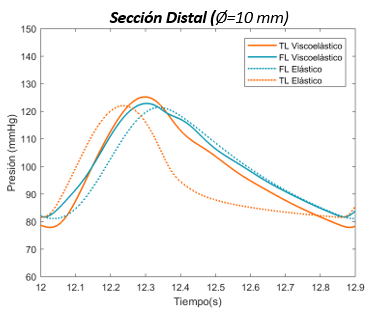
|
| Gráfica 29. Comparativa de presión entre modelo visco elástico y elástico. sección distal. Primer escenario |
| Gráfica 30. Comparativa de presión entre modelo visco elástico y elástico. sección proximal. Primer escenario |
| Sección | Coeficiente de Variación (Cv) entre el modelo elástico y viscoelàstico |
| Sección proximal TL | 12.9% |
| Sección proximal FL | 2.2% |
| Sección distal TL | 14.1% |
| Sección distal FL | 4.9% |
Las diferencias apreciables a primera vista del modelo visco elástico y elástico, es el comportamiento de la onda de cada uno. El primero, la onda refleja más expansión, el área bajo su curva es considerablemente mayor respecto al otro. (Tanto para el TL como para el FL) Se diferencia claramente la incisura dicrota en la sección proximal. Este modelo llega a su presión sistólica máxima de un modo más tardío respecto al modelo contrario, e incluso el pico máximo es menor. Esto hecho es un comportamiento razonable y esperado, que se explicó en el Apartado 4.3.1.
En el caso del elástico, la curva evoluciona de un modo lineal, llegando a su punto máximo y decreciendo sin nada apreciable. Ocurre lo mismo para la sección distal. El comportamiento lineal del modelo elástico está vigente, pues la onda crece y decrece más rápidamente que el modelo viscoso.
Respecto a los coeficientes de variación calculados, observamos que las ondas del TL son las que más presentan diferencia, alcanzando un valor de casi un 14%. Por el contrario, el FL presenta unas variaciones muy pequeñas, apenas llegando al 5%. Con esto, se podría valorar que las curvas se asemejan ciertamente, pues al tener una variación de aproximadamente 14%, significa que en un 86% si se muestran parecidas. No obstante, el comportamiento de la curva si es diferente, pues capta de un modo más claro, parámetros fisiológicos destacables.
- II. Escenario segundo mm, mm)
4.3.3.2. Presión. Segundo escenario
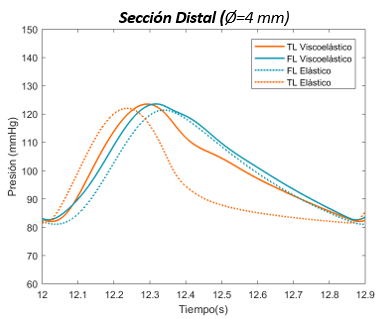
|
| Gráfica 31. Comparativa de presión entre modelo visco elástico y elástico. Sección distal. Segundo escenario |
| Gráfica 32. Comparativa de presión entre modelo visco elástico y elástico. Sección proximal. Segundo escenario |
| Sección | Coeficiente de Variación (Cv) entre el modelo elástico y viscoelàstico |
| Sección proximal TL | 20.1% |
| Sección proximal FL | 1.8% |
| Sección distal TL | 10.5% |
| Sección distal FL | 1.7% |
En el segundo escenario, ocurre igual que en el primero. Destaca el modelo visco elástico delante del elástico por el comportamiento de la onda. En este caso, la muesca dicrota se aprecia incluso más que en el caso anterior. Este modelo sigue presentando un área bajo la curva mayor respecto al otro, un punto máximo de presión que se alcanza más tarde (Gráfica 31), como el modelo elástico alcanza su presión sistólica máxima en los 12,23 segundos aproximadamente, y el modelo viscoso la alcanza en el punto 12,3 segundos. El comportamiento del modelo elástico se mantiene lineal en ambas secciones. Se captan en ambos modelos la propagación de la onda de pulso, siendo un poco menor, en el caso del modelo viscoso.
Tanto en la sección proximal como distal, la curva del FL del primer modelo es muy parecida a la del segundo modelo. Se observa por eso, que el coeficiente de variación entre ambas no llega al 2%. El verdadero lumen en cambio, presenta una variación un poco mayor, puesto que la forma de la onda es bastante diferente.
- III. Escenario tercero mm, mm)
4.3.3.3. Presión. Tercer escenario
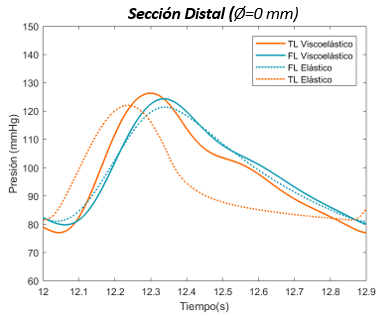
|
| Figura 33. Comparativa de presión entre modelo visco elástico y elástico. sección distal. Tercer escenario |
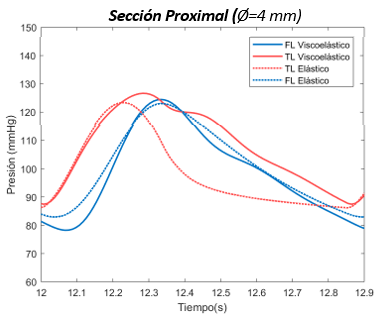
|
| Figura 34. Comparativa de presión entre modelo visco elástico y elástico. sección proximal. Tercer escenario |
| Sección | Coeficiente de Variación (Cv) entre el modelo elástico y viscoelàstico |
| Sección proximal TL | 25.7% |
| Sección proximal FL | 6.3% |
| Sección distal TL | 15.7% |
| Sección distal FL | 10.7% |
Las curvas de presión obtenidas en la sección proximal en el modelo elástico muestran un comportamiento lineal, una curva bien definida, sin apenas alteraciones. Se aprecia por un lado, el punto de presión sistólica –punto máximo- y el de presión diastólica –punto mínimo- tanto en el TL como en el FL, y por otro, hay un desfase pronunciado entre la onda del TL y el FL representando la propagación de onda del fluido.
En las curvas del modelo viscoelástico en dicha sección, se ven las características hemodinámicas de las que se hablava anteriormente, la aparición breve de la onda dicrótica. El comportamiento de las curvas en este modelo son más irregulares respecto a las elásticas, tanto en el FL como en el TL.
Los valores de presión que presentan se consideran normales, pues oscilan entre 125 mmHg de máximo y unos 80 mmHg de mínimo.
Al observar los valores obtenidos por el Cv vemos que hay cierta simulitud entre la sección distal y proximal del FL en ambos modelos (±entre 6% y 11%) , y que esta disminuye al tratarse del TL, pues el valor es mucho mayor (± entre 26% y 16%). Con esto, podría valorar que las curvas se asemejan ciertamente, pues al tener una variación de aproximadamente el 20%, significa que en un 80% si se muestran se parecen.
Tras la comparación de ambos modelos en los diferentes escenarios se observa un comportamiento similar dentro de cada modelo específico. En cada caso, la presión oscilaba entre los 120 mmHg como máximo y unos 80 como mínimo. En el caso del tercer escenario que la presión máxima y mínima se ve ligeramente alterada, se menciona la posible causa. (véase Apartado 4.3.2., Sección e) Finiquitando esta sección y la parte de resultados, cabe resaltar que se han obstenidos los resultados esperados en cuanto al comportamiento del sistema siendo este elástico o viscoso.
Conclusiones
Se ha presentado una herramienta numérica capaz de describir las principales características de la propagación del flujo sanguíneo a través del sistema cardiovascular. Esta herramienta es fácil de usar puesto que se puede acoplar con otros modelos computacionales, según la patología o la situación que se pretenda analizar.
A través de los diferentes capítulos de los que consta este trabajo, se ha expuesto el cómo representar el flujo sanguíneo y la presión en modelos de orden reducido. La principal ventaja de la formulación de estos modelos es que son computacionalmente barato y rápido, los parámetros del modelo se pueden modificar fácilmente y ofrece un bien equilibrio entre la precisión y el coste computacional cuando se requiere una evaluación global de la propagación de las ondas de presión y flujo dentro del sistema cardiovascular.
Sin embargo, el inconveniente que ofrecen estos modelos de orden reducido es que no permiten calcular características del flujo demasiado detalladas, o características hemodinámicas más significativas, como el esfuerzo cortante de la pared arterial y su deformación, entre otros. No obstante, ofrecen la información de un modo sencillo y veloz, y es relativamente fácil obtener y crear un modelo para cada situación. Se afirma esto, puesto que a lo largo del trabajo se ha visto que para elaborar el modelo se requieren parámetros como, la eyección cardíaca, la longitud y el radio de las arterias, el cumplimiento periférico, la resistencia periférica, la presión de salida, etc., que se pueden estimar a partir de mediciones in vivo o a partir de otros cálculos (como en este caso la eyección cardíaca que se aproximó con una sinusoide). Estos modelos, además, son muy útiles para realizar análisis de sensibilidades de parámetros o características fisiológicas, como, por ejemplo, la importancia de la rigidez arterial ante diferentes patologías.
Tras los resultados se demuestra, que el método numérico elaborado captura las principales características del comportamiento hemodinámico de la sangre, así como la propagación de las ondas de presión y flujo.
En el caso del modelo visco elástico, cuando se han utilizado los datos adecuados de cumplimiento de la pared, resistencia, inercia y condiciones de contorno, se ha podido capturar la muesca dicrota. Esto nos dice que este modelo es el que captura mejor el comportamiento real de los vasos sanguíneos.
Aunque, una de las dificultades del trabajo, y donde se ha invertido más tiempo, ha sido en el ajuste de los parámetros fisiológicos de los modelos.
Finalmente, añadir que estos modelos pueden ser usados como herramienta clínica ya que puede proporcionar información hemodinámica relativamente rápida, para una predicción vascular, hecho que ayudará en situaciones como la planificación de cirugías, mejora del diagnóstico para pacientes y simulación de otras patologías si fuese necesario. Se exponen más detalladamente a continuación.
Aplicaciones clínicas
Los avances en mejorar los modelos para la simulación del flujo sanguíneo tienen su aplicación más inmediata en los entornos clínicos en tres terrenos principales:
- 1. Prevención de enfermedades vasculares. En este caso, si una persona es sometida a revisión y se simula su flujo sanguíneo, será posible detectar anomalías en este y así poder actuar de forma temprana para corregirlas a tiempo.
- 2. Diagnóstico de enfermedades vasculares. Mediante la simulación de flujo sanguíneo de un paciente se puede obtener información sobre éste y así poder descubrir las posibles patologías relacionadas con sus variables mecánicas.
- 3. Facilidades durante la intervención quirúrgica del sistema cardiovascular. Como por ejemplo bypass, implantación de stents, etc. En general, el hecho de conocer el comportamiento del flujo sanguíneo es de ayuda para el diseño y la introducción de dispositivos en los vasos, ya que se conocería a priori al comportamiento hemodinámico.
Cabe destacar que, estos modelos pretenden facilitarle el trabajo dándole al médico herramientas que le ayuden a su toma de decisiones, nunca substituirlo.
Trabajo futuro
Como se ha comentado anteriormente una de las dificultades del trabajo fue el ajuste de los variables del modelo, para ello como trabajo futuro, se podría realizar un ajuste/análisis paramétrico de las mismas utilizando medidas reales de los pacientes. Se podría implementar un método de optimización para minimizar una función objetivo entre los datos reales (flujo o presión del paciente) y el simulado (modelo 0D), de manera de obtener las características fisiológicas del paciente más aproximadas.
Bibliografía
[1] A. Quarteroni and L. Formaggia. Mathematical modelling and numerical simulation of the cardiovascular system. 2002.
[2] C.G. Caro, T.J. Pedley, R.C. Schroter and W.A. Seed. The mechanics of the circulation. Oxford University Press, 1978.
[3] I. Kokalari, T. Karaja, and M. Guerrisi. Review on lumped parameter method for modeling the blood flow in systemic arteries. J. Biomedical Science and Engineering, 2013.
[4] J. Alastruey. Numerical modelling of pulse wave propagation in the cardiovascular system development, validation and clinical application. PhD thesis, Imperial College London, 2006.
[5] Williams & Warwick. Gray’s anatomy. 36th edition edition, 1980.
[6] L. Formaggia, A. Quarteroni, and A. Veneziani. Cardiovascular mathematics: Modeling and simulation of the circulatory system. 2009.
[7] J.D. Humphrey. The cardiovascular system. Biomechanics of Soft Tissue in Cardiovascular Systems, CISM(441), 2001.
[8] P. Segers, A. Qasem, T. De Backer, S. Carlier, P. Verdonck and A. Avolio. Peripheral ‘oscillatory’ compliance is associated with aortic augmentation index. Hypertension, 2001.
[9] P. Rudenick, B. Bijnens, P. Segers, A. Evangelista. Assesment of Wall Elasticity Variation on Intraluminal Haemodynamics in Descending Aortic Dissections Using a Lumped-Parameter Model. 2015.
[10] J. Wan, B. Steele, S.A. Spicer, S. Strohband, T.J.R. Hughes and C.A. Taylor. A one-dimensional finite element method for simulation-based medical planning for cardiovascular disease. Comp. Meths. Biomech. Biomed. Eng., 5(3), 195-206, 2002.
[11] P.A. Rudenick, M. Bordone, B.H. Bijnens, E. Soudah, E. Oñate, D. Garcia-Dorado and A. Evangelista. Influence of tear configuration on false and true lumen haemodynamics in type B aortic dissection, 2015.
[12] R. Gul. Mathematical Modeling and Sensitivity Analysis of Lumped-Parameter Model of the Human Cardiovascular System. PhD thesis, 2016.
[13] Noordergraaf A., Verdouw P.D. and Boom H.B.K. The use of an analog computer in a circulation model. Progress in Cardiovascular Diseases, 1963.
[14] C.D. Prevel, MD, Hani S. The extrinsic blood supply of the ulnar nerve at the elbow: An anatomic study. Journal of Hand Surgery Am., 18(3), 433-8, 1993.
[15] Phillips C., A simple lumped parameter model of the cardiovascular system. PhD thesis, Colorado State University Fort Collins, Colorado, 2011.
[16] Soudah E., Rudenick P., Bordone M., Bijnens B., García-Dorado D., Evangelista A. and Oñate, E. Validation of numerical flow simulations against in vitro phantom measurements in different type B aortic dissection scenarios. Computer methods in biomechanics and biomedical engineering, 8(8), 805-815, 2015.
[17] Rudenick P.A., Bordone M., Bijnens B.H., Soudah E. et al. A multi-method approach towards understanding the pathophysiology of aortic dissections—the complementary role of in-silico, in-vitro and in-vivo information. In: Statistical atlases and computational models of the heart. Berlin, pp 114–123, 2010.
[18] Thomas T. Tsai, M.D., Marty S. Schicht, M.S., Khalil Khanafer, PhD, Joseph L. Bull, PhD, Ramon Berguer, MD, PhD and Kim A. Eagle, MD. Tear size and location impacts false lumen pressure in an ex vivo model of chronic type B aòrtic dissection, 2007.
[19] Y.C. Fung. Mechanical properties of living tissues. Biomechanics, Springer, 1993.
[20] M. Catanho, M. Sinha, V. Vijayan. Model of Aortic Blood Flow Using the Windkessel Effect. 2012.
[21] L.F. Shampine and M.W. Reichelt. The Matlab ODE Suite, SIAM J. Sci. Comput., 18, 1–22, 1997.
[22] E. Soudah, E.Y.K. Ng, T.H. Loong, et al. CFD Modelling of Abdominal Aortic Aneurysm on Hemodynamic Loads using a Realistic Geometry with CT. Computational Mathematical Methods in Medicine, 2013:472564, 2013.
[23] Soudah E., Rossi R., Idelsohn S. and Oñate E. A reduced-order model based on the coupled 1D-3D finite element simulations for an efficient analysis of hemodynamics problems. Computational Mechanics, 54(4), 1013-1022, 2014.
[24] Keynes G. The Life of William Harvey. Oxford, Clarendon Press, 1978.
[25] Shim E.B., Sah J.Y. and Youn, C.H. Mathematical modeling of cardiovascular system dynamics using a lumped parameter method. Japanese Journal of Physiology, 54, 545-553, 2004.
[26] J. Calvo Plaza. Simulación del flujo sanguíneo y su interacción con la pared arterial mediante modelos de elementos finitos. Tesis Doctoral, 2006.
[27] Burattini R. and Natalucci S. Complex and frequency-dependent compliance of viscoelastic windkes sel resolves contradictions in elastic windkessel. Medical Engineering and Physics, 20, 502-514, 1998.
[28] Baumann E.D. Praxagoras de Kos. Janus 41, 167-185, 1937.
[29] O. Lewis. Praxagoras on Cos on arteries, pulse and pneuma: fragments and interpretation. 2017.
[30] Soudah E. Computational fluid dynamics indicators to improve cardiovascular pathologies. Thesis Doctoral, UPC, 2016.
Document information
Published on 18/03/20
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?