AbdulRahman (talk | contribs) m (AbdulRahman moved page Draft Shakir 302366137 to Review 223450771672) |
AbdulRahman (talk | contribs) (Tag: Visual edit) |
||
| Line 21: | Line 21: | ||
==1. Introduction== | ==1. Introduction== | ||
| − | <span style="text-align: center; font-size: 75%;">The undesired vibration can be eliminated by using active control methods. Over the last decade, considerable attention has been paid to the piezoelectric smart structures using for active vibration control. There are some previous studies reported in this piece of work. The simple cantilever beam’s active vibration control is investigated in [1-5] . Piezoelectric patches are mounted on the beams as actuators. With the purpose of sensing the vibration level, a strain-gage or another piezoelectric patch can be used. The identification system and placement control technique | + | <span style="text-align: center; font-size: 75%;">The undesired vibration can be eliminated by using active control methods. Over the last decade, considerable attention has been paid to the piezoelectric smart structures using for active vibration control. There are some previous studies reported in this piece of work. The simple cantilever beam’s active vibration control is investigated in [1-5] . Piezoelectric patches are mounted on the beams as actuators. With the purpose of sensing the vibration level, a strain-gage or another piezoelectric patch can be used. The identification system and placement control technique was utilized in [1]. The piezo patches and beam structure’s finite element model is constructed and the closed-loop control is applied in [2,3] . Also, Singh et al. [4] utilized the model of the beam and piezo-patches finite element, however, conducted modal control techniques. Xu and Koko [5] used the commercial finite element package ANSYS to state the findings. The control design was conducted in the space state that was set in the analysis of the finite element model. For the control design, the MATLAB as a system toolbox was utilized in their experiment. The sensor’s/actuator’s influence site was investigated. It was noticed that the site near the fixed end for the vibration control was better. Lim [6] investigated several modes for vibration control of a fixed square plate by using devices of location discrete sensor/actuator at maximum strain points. Quek et al. [7] introduced a typical placement method of pairs of piezoelectric sensor /actuator for the vibration control sealed compound plates. Xiamin et al. [8] used four bar linkage to investigate the active vibration control. The model of the finite element is applied and the reduced mode, robust </span> <math display="inline">{H}_{\infty }</math><span style="text-align: center; font-size: 75%;"> , and standard H∞ control methods are analyzed.Halim and Moheimani [9] investigated on a set of proposals to a criterion for ideal placement of a collected piezoelectric sensor-actuator pair on their supported plate by using modal and locative controllability. Vashist and Chhabra [10] found the optimal piezoelectric actuator’s locations by using an integer coded genetic algorithm GA on their plate where the singular value decomposition’s control matrix was used as a fitness function. It is observed nearly results of the frequency responses between experimental and Finite Element Method results. Yavuz et al.[11] analyzed a system of active vibration control’s closed loop with the purpose of suppressing the vibrations of the end-point. They established the system’s mathematical model by using the Lagrange equations. The digital solution is achieved through mixing the New-mark technique with the control action. They applied PID control action with the purpose of finding the value of the actuator signal at the appropriate time. Liu X. et al.[12] studied the piezoelectric actuators’ placement optimization and the membrane structure’s active vibration control. They designed the classical linear quadratic regulator controllers with the aim of suppressing the undesired vibration. Simulations findings indicated that the piezoelectric actuators’ optimal locations are influenced by the actuator’s additional mass and stiffness. Van et al.[13] developed a finite element model according to the theory of first–order shear deformation for active vibration control and optimal placement of laminated composite plates with linked pairs of distributed piezoelectric sensor/actuator. Baghaee et al. [14] developed the aero elastic panel flutter of the laminate composite plate includes two piezoelectric (MFC-type). They determined MFC actuator’s input voltage through the velocity or proportional feedback control algorithms according to the sensor output. Usman et al. [15] used piezoelectric MFC energy harvesting on the cantilever beam were joined with a downstream cylinder and placed stationary upstream cylinder before applied wind flow on both cylinders. Optimum spacing between two cylinders was identified three times the circular cylinder diameter. </span> |
| − | This work deals with the active vibration control analysis in smart composite beam structures by using ANSYS APDL codes. All nodes in the composite structure beam subjected to the boundary condition (exactly 1260 boundary condition), and by using different proportional control gain to control vibration suppression to two sets of the composite beams, (0/90) sets and (0/45) sets to reach the steady-state.From the obtained reslts | + | This work deals with the active vibration control analysis in smart composite beam structures by using ANSYS APDL codes. All nodes in the composite structure beam subjected to the boundary condition (exactly 1260 boundary condition), and by using different proportional control gain to control vibration suppression to two sets of the composite beams, (0/90) sets and (0/45) sets to reach the steady-state. From the obtained reslts t can be concluded that the technique is able to dump the vibration of the beam composite structure. |
==2. Simulation Method== | ==2. Simulation Method== | ||
Revision as of 14:57, 22 February 2020
Abstract
Piezoelectric Macro-Fiber Composite (MFC) utilization is increasing in engineering fields due to its strong actuation forces and high flexibility. In this paper, piezoelectric ( ) type (M8528-P1) patches are applied for active control on a cantilever composite beam. A linear coupled finite element model for piezoelectric MFC actuation with the composite beam was developed based on the APDL-ANSYS codes by using linear piezoelectric constitutive equations to studies smart composite beam behavior in open and closed loop cases. The results thus obtained are compared with different ply laminate by macro codes.In this the proportional type (kp) of control algorithms is utilized, and in the summary of work refined two sets of finite element models, The first set their laminates to have orientation (0 with 90) and others have orientation (0 with 45), when the control signal was applied with the gain (kp) to a system increases, the rise time generally decreases, that the actuator voltages for different control gain for all cases are observed with the increase in the proportional constant. The findings of this study indicate that the composite beams composed from (0/90)sets had reached to stability state faster than the composite beams composed from (0/45) sets.
Keywords:
MFC piezoelectric, smart composite beam, FEM (APDL Codes), Active vibration.
1. Introduction
The undesired vibration can be eliminated by using active control methods. Over the last decade, considerable attention has been paid to the piezoelectric smart structures using for active vibration control. There are some previous studies reported in this piece of work. The simple cantilever beam’s active vibration control is investigated in [1-5] . Piezoelectric patches are mounted on the beams as actuators. With the purpose of sensing the vibration level, a strain-gage or another piezoelectric patch can be used. The identification system and placement control technique was utilized in [1]. The piezo patches and beam structure’s finite element model is constructed and the closed-loop control is applied in [2,3] . Also, Singh et al. [4] utilized the model of the beam and piezo-patches finite element, however, conducted modal control techniques. Xu and Koko [5] used the commercial finite element package ANSYS to state the findings. The control design was conducted in the space state that was set in the analysis of the finite element model. For the control design, the MATLAB as a system toolbox was utilized in their experiment. The sensor’s/actuator’s influence site was investigated. It was noticed that the site near the fixed end for the vibration control was better. Lim [6] investigated several modes for vibration control of a fixed square plate by using devices of location discrete sensor/actuator at maximum strain points. Quek et al. [7] introduced a typical placement method of pairs of piezoelectric sensor /actuator for the vibration control sealed compound plates. Xiamin et al. [8] used four bar linkage to investigate the active vibration control. The model of the finite element is applied and the reduced mode, robust , and standard H∞ control methods are analyzed.Halim and Moheimani [9] investigated on a set of proposals to a criterion for ideal placement of a collected piezoelectric sensor-actuator pair on their supported plate by using modal and locative controllability. Vashist and Chhabra [10] found the optimal piezoelectric actuator’s locations by using an integer coded genetic algorithm GA on their plate where the singular value decomposition’s control matrix was used as a fitness function. It is observed nearly results of the frequency responses between experimental and Finite Element Method results. Yavuz et al.[11] analyzed a system of active vibration control’s closed loop with the purpose of suppressing the vibrations of the end-point. They established the system’s mathematical model by using the Lagrange equations. The digital solution is achieved through mixing the New-mark technique with the control action. They applied PID control action with the purpose of finding the value of the actuator signal at the appropriate time. Liu X. et al.[12] studied the piezoelectric actuators’ placement optimization and the membrane structure’s active vibration control. They designed the classical linear quadratic regulator controllers with the aim of suppressing the undesired vibration. Simulations findings indicated that the piezoelectric actuators’ optimal locations are influenced by the actuator’s additional mass and stiffness. Van et al.[13] developed a finite element model according to the theory of first–order shear deformation for active vibration control and optimal placement of laminated composite plates with linked pairs of distributed piezoelectric sensor/actuator. Baghaee et al. [14] developed the aero elastic panel flutter of the laminate composite plate includes two piezoelectric (MFC-type). They determined MFC actuator’s input voltage through the velocity or proportional feedback control algorithms according to the sensor output. Usman et al. [15] used piezoelectric MFC energy harvesting on the cantilever beam were joined with a downstream cylinder and placed stationary upstream cylinder before applied wind flow on both cylinders. Optimum spacing between two cylinders was identified three times the circular cylinder diameter.
This work deals with the active vibration control analysis in smart composite beam structures by using ANSYS APDL codes. All nodes in the composite structure beam subjected to the boundary condition (exactly 1260 boundary condition), and by using different proportional control gain to control vibration suppression to two sets of the composite beams, (0/90) sets and (0/45) sets to reach the steady-state. From the obtained reslts t can be concluded that the technique is able to dump the vibration of the beam composite structure.
2. Simulation Method
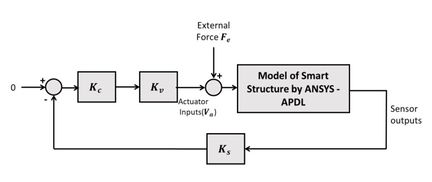
In this section, ANSYS software simulates active vibration control in the smart composite. Fig. 1 shows the block diagram of the obtained analysis. ANSYS/Multiphysics and ANSYS/Mechanical programs can be used for modelling structural fields with piezoelectric smart patches. Whereas is the force of vibration generated. The instant value of vibration producing force can be described at each time step. In the analysis below, it is taken as at and zero for other time steps. At a piezoelectric sensor location, the strain ( ε ) is calculated. Reference input for vibration cancellation is zero. , , and are respectively the variables the control, power and sensor amplification factors. and are taken as 250 and 30 by inspection, and is changed in the analyses below. Only the proportional control is applied. The proportional constant for the actuator voltage was obtained from the multiplication of . Therefore, the results are not affected by changing the values of , and and keeping their multiplication the same. To evaluate the performance the vibration control, the calculated deflection at a location, , is observed.
|
| Fig. 1: Block diagram of the analysis |
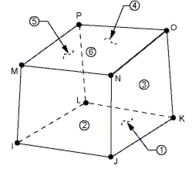
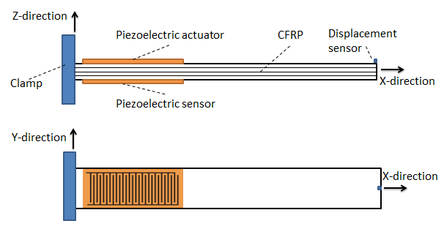
First, the structures of the beam type are considered. The configuration of the beam composite structure is shown in Fig. 2.
|
| Fig. 2: onfiguration for the structure of the beam type |
2.1 Material Properties
The Finite Element Analysis is used as the numerical modelling tool to simulate the dynamic characteristics of the composite structures by ANSYS macro codes, the macro file has been written by using APDL. The first step in the coding process defined model geometry by using direct mesh generation of smart structure. In first our system, a composite smart beam of size (400 mm x 28 mm ) and various thickness (1.59 mm, 2.12mm and 3.18mm) according to number of laminates, with ( ) piezoelectric patch actuator type (M8528-P1), these typically consist of an active area (85mm x 28 mm) with (0.3 mm) thickness, and it's embedded on the beam from (10 mm) on the fixed point, as shown in Table 1 for all cases.
2.2 Simulation procedures
In the First step,The beam structures type is taken and considered. Fig. 2 displays the configuration of the structure with sensor locations. The displacement value is taken from the displacement sensor and similarly, the strain value is taken from the strain sensor as the feedback.In here , the product of ANSYS /Multiphysics (version 18) was used to the structures of the smart compsoites model. The combination of the ANSYS modelling and solution into the control actions codes were achieved by ANSYS [16].
The composite smart structure beam is studied as indicated in Table 1.
| Table 1 Dimensions and distances of Composite beam structure | ||
| Case No. | Composite layers | Dimensions of the structure (mm) |
| 1 | (0/90/0) | 400x28x1.59 |
| 2 | (0/90/0/90) | 400x28x2.12 |
| 3 | (0/90/90/0) | 400x28x2.12 |
| 4 | (0/90/0/0/90/0) | 400x28x3.18 |
| 5 | (0/45/0) | 400x28x1.59 |
| 6 | (0/45/0/45) | 400x28x2.12 |
| 7 | (0/45/45/0) | 400x28x2.12 |
| 8 | (0/45/0/0/45/0) | 400x28x3.18 |
The macro file creates nodes and finite elements to the structure. In the first part, composite materials have been used element type SOLID185 layered structural elements for composite beam or plate part as shown in Fig. 3a, and element type (SOLID5) elements with (MASS21) were used in the second structure part for the piezoelectric part in the structure as shown in Fig. 3b [17]. Overall, these macro codes as shown in Table 2 indicate that defined element type of various materials.

|
|
| (a) | (b) |
| Fig. 3: (a) SOLID185 layered structural elements (b) SOLID5 elements | |
| Table 2 Element definition codes | |
| /PREP7 | ! start the preprocessing |
| ! Define Element type #1 | |
| ET,1,185 | ! chooses SOLID185 element for analysis composite material |
| KEYOPT,1,3,1 | ! Key option #3 = 1 LAYERED SOLID ELEMENTS |
| KEYOPT,1,2,2 | ! Key option #2 = 2 ENHANCED STRAIN FORMULATION |
| KEYOPT,1,8,1 | ! Key option #8 = 1 STORE DATA FOR ALL LAYERS |
| ! Define Element type #2 | |
| ET,2,solid5,3 | ! chooses SOLID5 element for analysis piezoelectric material |
| ET,3,mass21 | |
Therefore, an essential next step to confirming in three-dimensional composite material properties is assigned. As shown in Fig. 2. The structure is divided into two parts. The first part deals with composite material and the other part is actuator and all properties as shown in Table 3 ,and all that has been gained from [18][19]&[20].
| Table 3 Material properties of MFC and CFRP | ||||
| Material Properties | CFRP | MFC | ||
| Young’s modulus | 30.34 GPa | |||
| Young’s modulus | 15.86 GPa | |||
| Young’s modulus | 9.03 GPa | |||
| Shear modulus | 5.52 GPa | |||
| Poisson’s ratio | 0.31 | |||
| Poisson’s ratio | 0.30 | |||
| Density ρ | 5020 | |||
| Piezoelectric Stress constant ( ) | -3.47 | |||
| Piezoelectric Stress constant ( ) | 12.36 | |||
The ANSYS macro of the material properties is given in Table 4. First Material is represented by composite material (Carbon fiber reinforced polymer), and the second material is represented by the piezoelectric (MFC) actuator material.
| Table 4 Composite material properties codes | |||
| /PREP7
MP,EX,1,140E9 |
! Define Material 1# : E1= | ||
| MP,EY,1,8.75E9 | ! Define Material 1# : E2= | ||
| MP,EZ,1,8.75E9 | ! Define Material 1# : EZ=EY ; E3= | ||
| MP,GXY,1,7.2E9 | ! Define Material 1# : shear modulus xy-plane | ||
| MP,GYZ,1,6.21E9 | ! Define Material 1# : shear modulus xz-plane | ||
| MP,GXZ,1,7.2E9 | ! Define Material 1# : shear modulus yz-plane | ||
| MP,PRXY,1,0.3 | ! Define Material 1# : Poisson coefficient | ||
| MP,PRYZ,1,0.3 | ! Define Material 1# : Poisson coefficient | ||
| MP,PRXZ,1,0.3 | ! Define Material 1# : Poisson coefficient | ||
| MP,DENS,1,1550 | ! Define Material 1# : Density for composite material |
The number of composite layers, the thickness of layers, and orientation angles of fibers are assigned as macro APDL ANSYS codes for first material as given below in Table 5.
| Table 5 Orientation angles’ Composite layers codes | |
| SECTYPE,1,SHELL | set #1, [0/90/0] |
| SECDATA,0.53e-3,1,0 | ! 1st LAYER 1: Thk=0.53e-3m, THETA = 0 |
| SECDATA,0.53e-3,1,90 | ! 2nd LAYER 2: Thk=0.53e-3m, THETA = 90 |
| SECDATA,0.53e-3,1,0 | ! 3rd LAYER 4: Thk=0.53e-3m, THETA = 0 |
The second material piezoelectric actuator properties are given in Table 6 as macro ANSYS.
| Table 6 MFC properties codes | |
| ! Define dielectric constant | |
| MP,DENS,3,5020 | ! Density for MFC piezoelectric material |
| MP,PERX,3,15.586E-9 | ! Permittivity in X direction |
| MP,PERY,3,15.586E-9 | ! Permittivity in Y direction |
| MP,PERZ,3,11.79E-9 | ! Permittivity in Z direction |
| TB,PIEZ,3 | ! Define piezoelectric table |
| TBDATA,16,0 | ! e16 piezoelectric constant |
| TBDATA,14,0 | ! e25 piezoelectric constant |
| TBDATA,6,-3.47 | ! e32 piezoelectric constant |
| TBDATA,9,12.36 | ! e33 piezoelectric constant |
| TB,ANEL,3 | ! Define structural table |
After all dimensions and properties of both composite and piezoelectric properties are defined, the type of element is assigned for each type of material. SOLID185 layered structural elements are assigned for the composite part and SOLID5 elements are used for the piezoelectric part of the structure. Then, the static solution is analyzed to evaluate the initial deflections of each node and element. The model is discretized into finite elements model as shown in Fig. 4 .
The first three mode shapes and natural frequencies of the composite plates were obtained using APDL ANSYS macro codes. The obtained results were shown in the Fig. 5 .The first three natural frequencies are evaluated by the modal shape analysis method using ANSYS are (15.665 Hz), (94.17Hz) and (161.63Hz) respectively for the first case considered in the present study are shown in Fig. 5.
Fixed boundary conditions are described for the nodes are given in Table 7 as macro ANSYS.
| Table 7 Boundary conditions of composite beam codes | |
| CP,1,volt,all | ! set #1 of coupled degrees of freedom. |
The degrees of freedom of the top and bottom surfaces for piezo actuator and sensor are coupled simultaneously with volt by APDL ANSYS “CP” command. Modal analysis was performed to determine parameters from vibration data measures like the inherent dynamic characteristics of the system in forms of natural frequencies, mode shapes and damping factor, and so to determine time step [21].
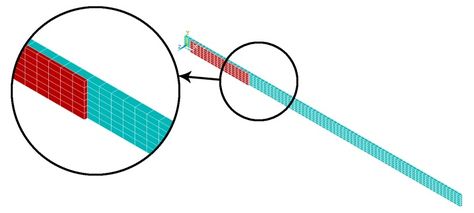
|
| Fig. 4: Finite element model |
Householder method (reduced method) can be used for the beam structures which have the solid coupled field in ANSYS. The time step is the incremental change in time and the time step is chosen by equation formula , where is the highest natural frequency to be considered. Table 8 shows the three natural frequencies for the undamped system. The first mode is considered to calculate the time step and is 0.0032, 0.0034, 0.0025, 0.00183, 0.00318, 0.0032, 0.0025, and 0.0018, for cases 1, 2, 3, 4, 5, 6, 7, and 8, respectively.

|
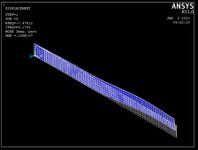
|

|
| 1st mode shape | 2nd mode shape | 3rd mode shape |
| Fig. 5: Mode shapes of first case | ||
In this study especially in the transient analysis part, Rayleigh damping coefficients (α and β) are defined as (β=2 α/3). The strain feedback is calculated at the selected sensor location, multiplied by to convert the strain feedback to voltage and then subtracted from zero to calculate the error signal.
The displacement feedback is also calculated at the selected sensor location, multiplied by in order to convert the displacement feedback to voltage, and also subtracted from zero to evaluate the error signal between the input and output.
| Table 8 Natural frequencies of system | ||||
| Case No. | Composite layers | First
(Hz) |
Second
(Hz) |
Third
(Hz) |
| 1 | (0/90/0) | 15.665 | 94.17 | 161.63 |
| 2 | (0/90/0/90) | 14.888 | 87.674 | 193.47 |
| 3 | (0/90/90/0) | 19.795 | 120.39 | 196.81 |
| 4 | (0/90/0/0/90/0) | 27.265 | 165.45 | 217.71 |
| 5 | (0/45/0) | 15.701 | 94.379 | 170.62 |
| 6 | (0/45/0/45) | 15.589 | 92.137 | 200.82 |
| 7 | (0/45/45/0) | 19.945 | 121.29 | 204.18 |
| 8 | (0/45/0/0/45/0) | 27.697 | 168.02 | 222.82 |
The difference between the input reference and the sensor signal is defined as the error signal. The error value is multiplied by for strain feedback and for displacement feedback and then both results are multiplied by the amplifier factor to determine at a given time step.
The macro part that enables the calculations for the analysis of the closed loop for t > ∆t is given in table 9.
| Table 9 Sensor feedback codes | |
| *do,tt,2*dt,ts,dt | !time loops |
| *get,uz-tip,node,nldm,u,z | !sensor feedback |
| err=ref-ks*uz-tip | !error signal |
| Vact=kp*kv*err | !actuator voltage |
| d,nv,volt,Vact | !Appling actuator volt |
| time,tt | |
| solve | |
| *enddo | |
3. Results and Discussion
There are two methods to deal with active vibration control. The first method is displacement feedback signals by using the displacement sensor, and the other method is strain feedback signals by using a piezoelectric strain sensor. Displacement feedback signals have been used for the displacement to suppression of vibration.
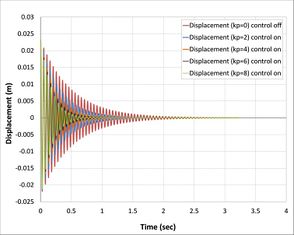
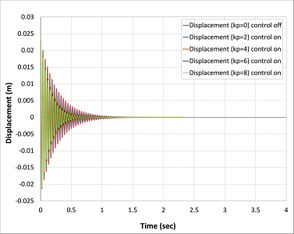
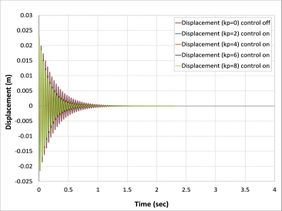
For classical controller (P) is the proportional control and gain (kp) is only the variable be changed. The present study has been used for (2,4,6, and 8) kp value. The open-loop and closed-loop responses of the tip displacement are shown in Fig.s 6(a), 6(b),6(c), and (6)d, respectively, by using APDL ANSYS. From the graph, it is found that the open-loop response vibrates a lot at a time of more than 5 sec in first Fig. 6(a), 4 sec in second Fig. 6(b), 3.8 in third Fig. 6(c), and 1.25 sec in the last Fig. 6(d) [22] . While in the first case, composite laminates consist of three-ply (0/90/0) the closed-loop responses by using classical controller when we took into consideration only proportional part effects in PID control shows settles at a time 1.4 sec, 0.85 sec, 0.75 sec and 0.7 sec, respectively, proportional gain (kp) is 2, 3, 6, 8, which demonstrate that three recent responses of the system will be near each other. This reduction in the time compare with the first case is due to the increase in the number of composite layers and, at the same time, increase in the strength properties of the beam is observed.

|
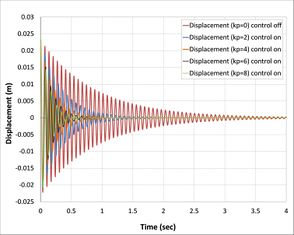
| |
| (a) CFRP (0/90/0) | (b) CFRP (0/90/0/90) | |
|
| |
| (c) CFRP (0/90/90/0) | (d) CFRP (0/90/0/90/0/90) | |
| Fig. 6: Open loop and closed loop responses of composite beam of tip displacement.
| ||
However, the evidence for this relationship is conclusive have been retrived from PID rules, with increasing the Proportional range, the vibration converges slowly and settling time increases. On the other side, the controlling signal has been decreasing by increasing value of the proportional constant that takes part in PID and neglected integral and derivative part. Whereas in the second case, composite laminates consist of four plies (0/90/0/90), the closed-loop responses or all proportional gain (kp) shown as in Fig. 6(b) is near results with first case because effect of fourth ply is smaller (90 degree) composite ply with beam, in the fourth case which demonstrate that control responses of the system will be near each other and this reduction in the time compare with others is due to the increase in the number of composite layers and in the same time increase in the strength properties of the beam. Based on the results it has been noted that an increase in laminates of composite plate decreases the vibration and time stability of the system.
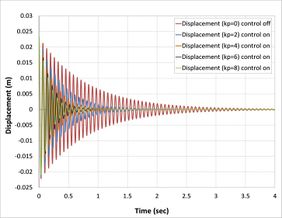
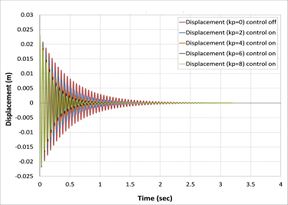
For Amplitude comparison between two sets of composite materials beam structures, first set consist of (0-90) degrees of laminates and another set consist of (0-45) degrees of laminates. Based on the responses that were simulated with high accuracy using the proportional gain formulation. As shown in Fig.s 6 and 7, all curves nearly have the same shape, but speed to reach the stable case in the second set is smaller than the first set. The reason is attributed due to the greater flexural strength for the second compared to the former.
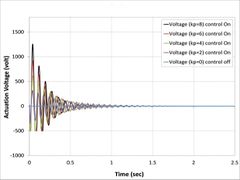
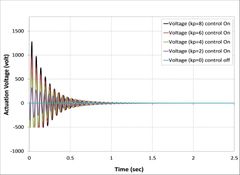
Piezoelectric MFC have a maximum voltage so it is peak to peak voltage, while peak voltage is the voltage from the zero horizontal axis line to the top of the waveform, the peak to peak voltage is the voltage of the one cycle of a wave, all the way from the peak of the negative side to the peak of the positive side [23]. Maximum voltage for MFC to be applied is (2000 volt) for the piezoelectric actuator. The uncontrolled and controlled responses obtained by actuation voltage can be seen in Figs. 8a, 8b, 8c, 8d, 8e, 8f, 8g, and 8h. From the graph, It has been observed that in the open-loop response was nil because in the open-loop there is not a link between vibrate response and actuator.

|
|
| (a) CFRP (0/45/0) | (b) CFRP (0/45/0/45) |
|
|
| (c) CFRP (0/45/45/0) | (d) CFRP (0/45/0/45/0/45) |
| Fig. 7: Open loop and closed loop responses of composite beam of tip displacement | |
On the other hand, in all cases when the control signal was applied with the gain to a system increases, the rise time generally decreases present in Fig. 8, that the actuator voltages for different control gain for all cases are observed increase with a proportional constant. While kp=8 has the highest value of actuator voltage is observed in all cases [24].
As can be seen from the Fig.s 8(b), 8(c), 8(d), 8(f), 8(g), and 8(h) the minimum value of actuator voltage is (-500V) and smaller than this volt by APDL-ANSYS macro file has been changed to (-500 Volt) because sinusoidal voltage of piezoelectric MFC-P1 is worked between (-500 volt) to (+1500 Volt) voltage cycle at 0.1 Hz was output by a voltage amplifier [25].
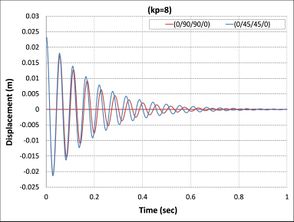
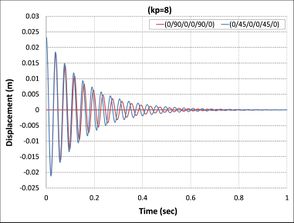
Another important finding was that Effect of fiber orientations of composite laminate layers on active vibrations, as shown in Fig. 9 the composite beams composed of laminates (0/90/0) , (0/90/0/90) , (0/90/90/0) , and (0/90/0/0/90/0) reach to stability faster than the composite beams composed of laminates (0/45/0) , (0/45/0/45) , (0/45/45/0) , and (0/45/0/0/45/0) because the first set has higher relaxation modulus than second sets [26] .

|

|
| (a) | (b) |
|
|
| (c) | (d) |
| Fig. 9: compared between two set similar composite beam | |
4. Conclusions
A FEM for piezoelectric with composite beam structure was proposed to simulate model dynamic, and the electrical model of piezoelectric which permitted the simulations of type ( ) effects. The performance of the composite beam structure is improved when piezoelectric type M8528(P1) is used. It is shown that the classic controller provides in increasing control gain (kp) better active damping than low control gain, especially at kp=8.
The active control capability of such composite beam is analyzed using a simple control strategy. Overall, these controlled responses show that, although all different composite laminate plates are subjected to the same intensity of mechanical load. The observed decrease in the vibration of the composite plate might be explained by the increase in the proportional gain in PID control on all cases composite laminate plate, while at the same time decreasing the voltage actuator of piezoelectric, the model can be used for more investigations with general composition, applied loads, and another control method. The final Objectives of analysis and modelling are the minimisation of weight (or mass) of the beam structure under behaviour constraints, increasing the performance of the piezoelectric actuator and maximisation natural frequencies of the vibration modes. However, given the immersed short time for each case, but caution must be taken the difference between two similar different in orientation laminate, two refined finite element models based 0/90 laminate set and 0/45 laminate set, for the analysis of laminated beam with embedded surface bonded piezoelectric laminae have been presented. The evidence from this study suggests the composite beams composed from (0/90) sets had reached stability state faster than the composite beams composed from (0/45) sets.
References
[1] Manning, W.J., Plummer, A.R. and Levesley, M.C. Vibration control of a flexible beam with integrated actuators and sensors . Smart Materials and Structures, 9(6), p.932, 2000.
[2] Gaudenzi, P., Carbonaro, R. and Benzi, E. Control of beam vibrations by means of piezoelectric devices: theory and experiments . Composite structures, 50(4), pp.373-379, 2000.
[3] Bruant, I., Coffignal, G., Lene, F. and Verge, M. Active control of beam structures with piezoelectric actuators and sensors: modeling and simulation . Smart materials and structures, 10(2), p.404, 2001.
[4] Singh, S.P., Pruthi, H.S. and Agarwal, V.P. Efficient modal control strategies for active control of vibrations . Journal of Sound and Vibration, 262(3), pp.563-575,2003.
[5] Xu, S.X. and Koko, T.S. Finite element analysis and design of actively controlled piezoelectric smart structures . Finite elements in analysis and design, 40(3), pp.241-262 , 2004.
[6] Lim, Y.H. Finite-element simulation of closed loop vibration control of a smart plate under transient loading . Smart Materials and Structures, 12(2), p.272, 2003.
[7] Quek, S.T., Wang, S.Y. and Ang, K.K. Vibration control of composite plates via optimal placement of piezoelectric patches . Journal of intelligent material systems and structures, 14(4-5), pp.229-245, 2003.
[8] Xianmin, Z., Changjian, S. and Erdman, A.G. Active vibration controller design and comparison study of flexible linkage mechanism systems . Mechanism and Machine Theory, 37(9), pp.985-997, 2002.
[9] Halim, D. and Moheimani, S.R. An optimization approach to optimal placement of collocated piezoelectric actuators and sensors on a thin plate . Mechatronics, 13(1), pp.27-47, 2003.
[10] Vashist, S.K. & Chhabra, D. Optimal placement of piezoelectric actuators on plate structures for active vibration control using genetic algorithm , In Active and Passive Smart Structures and Integrated Systems , International Society for Optics and Photonics, , 9057, p. 9, 2014.
[11] Yavuz, Ş., Malgaca, L. and Karagülle, H. Analysis of active vibration control of multi-degree-of-freedom flexible systems by Newmark method . Simulation Modelling Practice and Theory, 69, pp.136-148 , 2016.
[12] Liu, X., Cai, G., Peng, F. and Zhang, H. Piezoelectric actuator placement optimization and active vibration control of a membrane structure . Acta Mechanica Solida Sinica, 31(1), pp.66-79. https://doi.org/ 10.1007/s10338-018-0005-y, 2018.
[13] Van Tham, V., Quoc, T.H. and Tu, T.M. Optimal placement and active vibration control of composite plates integrated piezoelectric sensor/actuator pairs . Vietnam Journal of Science and Technology, 56(1), p.113, 2018.
[14] Baghaee, M., Farrokhabadi, A. and Jafari-Talookolaei, R.A. Modeling, analysis, and control of MFC sandwiched laminate panel flutter with general layups and arbitrary boundary conditions . Composite Structures, 223, p.110940, 2019.
[15] Usman, M., Hanif, A., Kim, I.H. and Jung, H.J. Experimental validation of a novel piezoelectric energy harvesting system employing wake galloping phenomenon for a broad wind spectrum . Energy, 153, pp.882-889,2018.
[16] ANSYS, ANSYS Mechanical APDL Basic Analysis Guide/ANSYS help, release 15.0 2013, Inc., Canonsburg, PA, 2017.
[17] Kamel, M.A., Ibrahim, K. and Ahmed, A.E.M. Vibration control of smart cantilever beam using finite element method. Alexandria Engineering Journal, 58(2), pp.591-601,2019.
[18] Trindade, M.A. and Benjeddou, A. Finite element characterisation of multilayer d31 piezoelectric macro-fibre composites . Composite Structures, 151, pp.47-57,2016.
[19] Vijay Kumar, G., Raja, S., Prasanna, K.B. and Sudha, V. Finite element analysis and vibration control of a deep composite cylindrical shell using MFC actuators . Smart Materials Research, 2012.
[20] Smart Materials Corporation. (Accessed Nov 2019). Actuator and sensor ,Available online: https://www.smart-material.com/MFC-product-P1.html
[21] Jimin He and Zhi-Fang Fu , Modal Analysis, Linacre House, Jorden Hill, Oxford , 2001.
[22] Huang, B., Kim, H.S. and Youn, B.D. Active vibration control of smart composite laminates with partial debonding of actuator . International Journal of Precision Engineering and Manufacturing, 16(4), pp.831-840, 2015.
[23] Ian Sinclair . Passive Components for Circuit Design, Linacre House, Jordan Hill, Oxford OX2 8DP, 2004.
[24] Garcia-Segura, T., Yepes, V., Marti, J.V. and Alcala, J. Optimization of concrete I-beams using a new hybrid glowworm swarm algorithm . Latin American Journal of Solids and Structures, 11(7), pp.1190-1205, 2014.
[25] Wu, M., Yuan, X., Luo, H., Chen, H., Chen, C., Zhou, K. and Zhang, D. Enhanced actuation performance of piezoelectric fiber composites induced by incorporated BaTiO3 nanoparticles in epoxy resin . Physics Letters A, 381(19), pp.1641-1647, 2017.
[26] Rony Das. Stress relaxation of ehermostting prepreg composites during cure ,MSc. thesis , Bangladesh University of Engineering and Technology, 2008
Document information
Published on 22/04/20
Accepted on 13/04/20
Submitted on 21/02/20
Volume 36, Issue 2, 2020
DOI: 10.23967/j.rimni.2020.04.001
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?