| Line 1,427: | Line 1,427: | ||
<div id="cite-16"></div> | <div id="cite-16"></div> | ||
| − | '''[[#citeF-16|[16]]]''' | + | '''[[#citeF-16|[16]]]''' Villota, A., Codina, R. (2018) "Approximation of the shallow water equations with higher order finite elements and variational multiscale methods", Volume 34 (1). Revista International de Métodos Numéricos para Cálculo y Diseño en Ing. 1–25 |
<div id="cite-17"></div> | <div id="cite-17"></div> | ||
| − | '''[[#citeF-17|[17]]]''' | + | '''[[#citeF-17|[17]]]''' Hirsch, J. J. (2007) "Water Waves: The Mathematical Theory with Applications", Volume. Interscience Publishers, Edition |
<div id="cite-18"></div> | <div id="cite-18"></div> | ||
| − | '''[[#citeF-18|[18]]]''' | + | '''[[#citeF-18|[18]]]''' Blazek, J. (2001) "Computational fluid dynamics: principles and applications.". Elsevier Science Ltd, 1 th Edition |
<div id="cite-19"></div> | <div id="cite-19"></div> | ||
| − | '''[[#citeF-19|[19]]]''' | + | '''[[#citeF-19|[19]]]''' Versteeg, H.K. and Malalasekera, W. (2007) "An Introduction to Computational Fluid Dynamics. The finite volume method". Pearson Education Limited, 2 th Edition |
<div id="cite-20"></div> | <div id="cite-20"></div> | ||
| − | '''[[#citeF-20|[20]]]''' | + | '''[[#citeF-20|[20]]]''' Maliska, C. R. (2013) "Transferência de Calor e Mecânica dos Fluidos Computacional". LTC, 2 th Edition |
<div id="cite-21"></div> | <div id="cite-21"></div> | ||
| − | '''[[#citeF-21|[21]]]''' | + | '''[[#citeF-21|[21]]]''' Patankar, S. (1980) "Numerical heat transfer and fluid flow". Hemisphere Publishing Corporation, Edition |
| + | |||
<div id="cite-22"></div> | <div id="cite-22"></div> | ||
| − | '''[[#citeF-22|[22]]]''' | + | '''[[#citeF-22|[22]]]''' MacCormack, R. W. (1969) "The effect of viscosity in hypervelocity impact cratering", Volume. American Institutue Aeronautics Astronautics 69–354 |
<div id="cite-23"></div> | <div id="cite-23"></div> | ||
| − | '''[[#citeF-23|[23]]]''' | + | '''[[#citeF-23|[23]]]''' Gabutti, B. (1983) "On two upwind finite-difference schemes for hyperbolic equations in non-conservative form", Volume 11. Comput. Fluids 3 207–230 |
<div id="cite-24"></div> | <div id="cite-24"></div> | ||
| − | '''[[#citeF-24|[24 | + | '''[[#citeF-24|[24]]]''' Porto, R. M. (2006) "Hidráulica Básica". EESC-USP, 4 th Edition |
| − | + | ||
| − | + | ||
| − | + | ||
Revision as of 19:43, 21 August 2019
Abstract
Este trabalho apresenta a simulação hidráulica do escoamento em um reservatório, utilizando o método dos volumes finitos para resolver o sistema de equações que modelam o fluxo bidimensional em águas rasas, negligenciando as tensões tangenciais. Para resolver as equações, utilizou-se um esquema híbrido de volumes finitos. A solução do sistema de equações linearizadas foi obtida por implementação computacional do método iterativo de Gauss-Seidel. Para ilustrar a aplicação do esquema numérico em engenharia hidráulica, apresenta-se o estudo do escoamento em um reservatório subterrâneo com pilares internos, cujo fluxo é gerado pela abertura de dois portões de saída. O código desenvolvido permite a análise temporal do volume e do fluxo no reservatório, a interpretação gráfica do fenômeno físico investigado bem como o cálculo da precisão do modelo. Os resultados obtidos mostram a interpretação física esperada, boa concordância com os dados da literatura, boa precisão, estabilidade e baixo custo computacional.
keywords
Equações de águas rasas, Volumes Finitos, Interpolação híbrida, Estabilidade numérica, Simulação de leito seco, Reservatório de contenção.
HYBRID NUMERICAL SCHEME FOR SIMULATION OF TRANSIENT FLOW IN A PLUVIAL WATER RESERVOIR
Abstract
This work presents the numeric simulation of flow in a reservoir, using the finite volume method for solver the system of equations that model the two-dimensional flow in shallow water, neglecting the tangential tensions. The solution of the system of linearized equations was obtained by computational implementation of the Gauss-Seidel iterative method. To illustrate the application of the numerical scheme in hydraulic engineering, it was considered the study of flow in an underground reservoir with internal pillars, whose flow is generated by the opening of two outlet gates. The employed code allowed the temporal analysis of the volume and the flow in the reservoir, the graphical interpretation of the investigated physical phenomenon as well as, the calculation of the precision of the model. The results obtained show the expected physical interpretation, good agreement with literature data, good precision,stability and low computational cost.
Keywords: Shallow water equations, Finite volumes, Hybrid interpolation, Numerical stability, Dry bed simulation, Containment reservoir.
1 Introdução
A ocorrência ou agravamento de inundações nas grandes cidades, bem como a quebra de barragens, tornaram-se problemas cada vez mais recorrentes, causando mortes e fortes impactos ambientais. Nesse cenário, fica evidente a necessidade de conhecimento prévio do comportamento dos fluxos de superfície livre e simulações de abertura de comportas de barragens para manejo de recursos hídricos, avaliação de riscos e usos para obtenção de melhor disponibilidade visando a preservação ambiental. Para tanto, é necessário utilizar metodologias que possam descrever as variáveis hidrodinâmicas envolvidas, como campo de velocidade do fluxo, turbulência e mudanças temporais na altura da superfície da água [1,2]. Em [3] sugere-se o uso de modelos matemáticos para entender os padrões de fluxo em corpos de água. Modelos matemáticos adequados são ferramentas úteis no gerenciamento de recursos hídricos, pois reduzem o tempo de análise, custos e riscos envolvidos em levar dados experimentais em fluxos reais auxiliando na tomada de decisões e na definição de ações corretivas diante de vazamentos iminentes. Matematicamente, os fluxos de superfície livre podem ser descritos de várias maneiras. Uma abordagem mais simples e muito aplicada é dada pelas Equações de Águas Rasas, que representam uma simplificação das Equações de Navier-Stokes e é aplicável aos fluxos nos quais as tensões e acelerações verticais podem ser negligenciadas sem prejuízo do resultado. Essas equações são derivadas por meio da integração das equações governantes (Navier-Stokes e Continuidade) na direção vertical. Sua derivação está fora do escopo deste trabalho, mas pode ser vista em detalhes em [4] . Esse sistema de equações, embora definido em um domínio bidimensional, fornece a altura da coluna de água e as componentes de velocidade em um fluxo instável. No entanto, a obtenção de uma solução analítica para o sistema de equações de águas rasas é, na maioria dos casos, uma tarefa difícil, pois trata-se de um conjunto de equações diferenciais parciais hiperbólicas não lineares com termos fontes. O que requer um tratamento numérico robusto para evitar instabilidades numéricas. Ao longo das últimas três décadas, muitos avanços foram realizados na solução numérica das equações de águas rasas para simulação de escoamentos unidimensionais aplicados a hidráulica fluvial em rios, canais e tubulações [5,6,7,8,9], e modelos bidimensionais aplicados à análise de escoamentos causados pela abertura instantânea de comportas e ruptura de barragens [10,11,12,13,14]. Em [10] utilizaram esquemas explícitos de diferenças finitas, na discretização das equações de águas rasas bidimensionais, adicionando condições de estabilidade e viscosidade artificial para suavizar as oscilações de alta frequência. Para validar, os esquemas discretos foram aplicados em um problema típico de engenharia hidráulica: abertura parcial de uma barragem e passagem de uma onda de inundação através de uma contração do canal, adotando a razão entre o nível de água a jusante e à montante como sendo, . Os resultados dos diferentes esquemas foram comparados e a ocorrência de oscilações numéricas foi observada, evidenciando a necessidade de se utilizar esquemas implícitos. O estudo de caso apontado em [10] foi analisado por [15] usando um esquema de elementos finitos de alta ordem e uma melhoria na relação para foi obtida, buscando simular a condição de leito seco em uma determinada região do domínio. Em [12] usaram dados experimentais em um evento de quebra de barragem para verificar a precisão, estabilidade e confiabilidade de uma solução numérica das equações de águas rasas obtidas por um esquema de volumes finitos bidimensional. O modelo numérico permitiu uma precisão de segunda ordem, tanto no espaço como no tempo, acarretando porém um alto custo computacional, apresentando algumas discrepâncias entre os resultados reais dos medidores e os resultados numéricos nos pontos pesquisados. Os autores destacam a necessidade de simular a propagação de uma onda de inundação para um fundo seco e áspero e otimizar o algoritmo para reduzir o tempo de computação. Um esquema de volumes finitos não estruturado para malhas triangulares para simular fluxos bidimensionais instáveis em águas rasas com frentes molhadas/secas sobre topografia complexa é apresentado em [11]. Utiliza-se em [11] para o esquema temporal o método explícito de Runge-Kutta e para o espacial a malha não estruturada. Comparações satisfatórias foram obtidas com dados mensurados e numéricos. Todavia, os autores sugerem a incorporação de um procedimento de escalonamento num esquema implícito temporal, e uma implementação paralela do algoritmo, a fim de reduzir o tempo computacional. A eficiência de um esquema implícito de volumes finitos é explorada em [13] para simulação de fluidos em águas rasas bidimensionais, com frentes secas/molhadas. Adotou-se em [13] um tratamento complexo para a discretização espacial, fazendo uso de uma malha não estruturada flexível para obter um melhor ajuste à geometrias irregulares. No entanto, é feito ressalvas quanto ao tempo computacional para obtenção da solução por esquemas implícitos, pois embora um método implícito normalmente exija menos etapas da solução, cada uma exige mais tempo computacional do que as soluções obtidas por um esquema explícito. Os autores apontam a necessidade de se utilizar um solucionador de matrizes que com um número reduzido de iterações alcance a convergência. Neste contexto, o objetivo principal deste trabalho é formular um esquema híbrido e totalmente implícito de volumes finitos para discretização das equações de águas rasas, a fim de obter uma solução numérica estável com um algoritmo iterativo otimizado, com convergência rápida e baixo custo computacional, para aplicação na simulação de fluxos bidimensionais transitórios em topografias complexas (com declives e sujeitos a resistência ao fluxo). Condições iniciais descontínuas representando leitos úmidos/secos foram adotadas. Para tanto, o trabalho está organizado da seguinte forma: A seção 2 apresenta as equações hiperbólicas, que regem a natureza das águas rasas, considerando as perdas de atrito e declives da topografia do domínio computacional e detalhando a configuração numérica destas equações; na seção 3, o modelo é validado e uma comparação é feita com os resultados obtidos com o trabalho apresentado em [10]. A robustez da solução numérica é verificada com uma extrapolação na relação para , na seção 4; o esquema é aplicado na análise de um problema hidráulico real na seção 5 e; as conclusões são apresentadas na seção 6.
2 Modelo Matemático e Solução Numérica
Na análise do escoamento bidimensional transiente em um canal, cuja topografia do fundo é descrita por uma superfície , busca-se determinar o nível do fluido de superfície livre e o campo de velocidade do fluxo para cada instante de tempo , conforme Fig. 1.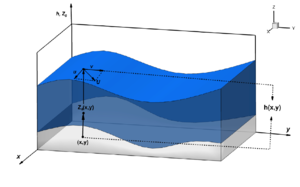
|
| Figure 1: Notação adotada na análise de fluxo em águas rasas |
2.1 Sistema de Equações Governantes
O sistema de equações diferenciais que descreve o escoamento hidrostático de um fluido incompressível em águas rasas com superfície superior livre é obtido pela integração ao longo da profundidade das equações tridimensionais que modelam a quantidade de movimento e conservação de massa num escoamento, assumindo distribuição de velocidade uniforme na direção vertical. Como em [3], adota-se as seguintes simplificações: (i) a distribuição de pressão na vertical é puramente hidrostática; (ii) não há contribuições laterais ao escoamento no reservatório analisado; (iii) a massa específica e a viscosidade do fluido no reservatório não sofrem variações significativas ao longo do tempo e do espaço; (iv) as tensões tangenciais são desprezíveis. Deste modo, as equações governantes do modelo hidrodinâmico, também ditas equações de águas rasas ou equações bidimensionais de Saint Venant, podem ser escritas na forma conservativa (com os fluxos dentro do sinal da derivada):
|
|
(1) |
|
|
(2) |
|
|
(3) |
onde e representam as componentes cartesianas nas direções longitudinal e transversal, respectivamente; é profundidade da água no reservatório; e são as componentes cartesianas da velocidade; é a aceleração da gravidade, é o tempo, e e são os declives do fundo do reservatório definidos como:
|
|
(4) |
enquanto os declives de resistência ao escoamento (perda de energia), nas direções e , respectivamente, são dadas por:
|
|
(5) |
onde é o coeficiente de rugosidade de Manning, que quantifica o atrito do fluxo com o fundo do canal. As equações de águas rasas (1) - (3) não possuem solução analítica fechada, portanto, uma abordagem numérica é empregada para resolvê-las de forma discreta e linearizada, onde o domínio é dividido em um número finito de células resultando em um sistema linear algébrico que é resolvido por um algoritmo computacional apropriado codificado em FORTRAN 90. Neste estudo, diferentes condições de contorno e topografia de fundo foram impostas para verificar a robustez e aplicabilidade do código. Na etapa inicial, o nível da água é sempre conhecido e todas as velocidades são iguais a zero para todo o domínio. Essas condições estão detalhadas nas Subseções 3.1 e 3.2.
2.2 Discretização do domínio e linearização das equações governantes
A solução numérica do modelo hidrodinâmico descrito pelas equações (1) - (3) é obtida por meio do método dos volumes finitos (MVF). Os fundamentos matemáticos e físicos do MVF são bem discutidos por [16], [17], [18] e [19]. De acordo com [20], o MVF consiste na integração espacial e temporal das equações diferenciais na forma conservativa (com todos os fluxos envolvidos pelo operador derivada) em um volume genérico de controle. O sistema de equações (1) - (3) é integrado espacialmente (sobre um volume de controle retangular) e no tempo (de a ) e é empregado para a integração temporal a seguinte aproximação numérica:
|
|
(6) |
Adota-se aqui uma notação mais compacta:
|
|
(7) |
E assim, a Eq. (6) pode ser reescrita como:
|
|
(8) |
Neste artigo, adota-se a formulação totalmente implícita, , ou seja, todas as derivadas são avaliadas no nível de tempo . Com uma implementação mais complexa, a formulação totalmente implícita é limitada apenas pela precisão e não sofre instabilidades numéricas devido à mudança de coeficientes de sinal pela variação do intervalo de tempo. E assim, permite o uso de etapas de tempo maiores com menor tempo de computação. Esse é um método incondicionalmente estável no tempo. Obviamente, esta estabilidade pode ser alterada devido às não linearidades do acoplamento e ao comportamento dos termos de fontes, como a perda de energia devido à declividade, o que pode gerar oscilações numéricas. Portanto, faz-se necessário um tratamento cuidadoso na obtenção de uma solução numérica estável e também precisa. A derivada temporal é avaliada com uma aproximação de Euler regressiva de ordem:
|
|
(9) |
onde representa uma variável. Na integração espacial é utilizado o Teorema Fundamental do Cálculo para reescrever as integrais das equações (1) - (3) como um sistema de equações constituído pelos valores das variáveis avaliadas nos pontos de integração , que por sua vez, são avaliados por funções de interpolação. Para o cálculo destes valores, adota-se uma combinação dos esquemas de diferenciação central de ordem (CDS - Central Differencing Scheme) e um esquema upwind (UDS - Upwind Differencing Scheme) de ordem. Na interpolação central, os valores das variáveis nas faces do volume de controle são dados pelo valor médio dos centróides vizinhos, isto é,
|
|
(10) |
No esquema upwind, os valores das variáveis nas faces do volume de controle são dados considerando primeiramente a direção do fluxo que transporta alguma propriedade do centróide vizinho para a face onde o fluxo é avaliado, por exemplo,
|
|
(11) |
O sistema (1) - (3) apresenta produtos de variáveis envolvendo , e . Esta característica é a natureza não-linear das equações de Saint-Venant e uma das razões pelas quais não existe uma solução analítica para problemas complexos de águas rasas, e assim, o sistema deve ser linearizado para permitir que o método numérico gere um sistema linear resolvido por qualquer solucionador linear. A linearização é feita considerando no produto de variáveis apenas uma delas como a variável ativa, e as outras são constantes ou variáveis secundárias calculadas a partir da condição inicial da iteração de looping do tempo anterior e/ou do último passo de tempo, por exemplo,
|
|
(12) |
onde neste exemplo, o índice representa os valores disponíveis do cálculo anterior e esses valores são usados para calcular o coeficiente da matriz para a variável ativa . Naturalmente, outras equações estão disponíveis para resolver e como a variável ativa (ou variável principal), e estas são empregadas para calcular cada coeficiente, assim, quando uma nova solução é alcançada, um novo cálculo é iniciado e novos coeficientes são definidos, e uma nova solução é executada até a convergência. Na combinação CDS/UDS, o esquema UDS é escolhido para a variável principal e a aproximação CDS para a variável secundária conhecida, por exemplo na integral da Eq. (1) o UDS é usado para a variável principal , e para e é aplicada a interpolação CDS usando os valores nodais vizinhos conhecidos do nó . Todos os valores nas faces são funções dos valores nodais , usando coeficientes que representam o sinal das componentes e nas faces do volume de controle, isto é, a direção do vetor de velocidade:
|
|
(13) |
|
|
(14) |
|
|
(15) |
|
|
(16) |
onde,
|
|
(17) |
|
|
(18) |
Portanto, a partir da formulação totalmente implícita e da interpolação híbrida CDS/UDS, a equação algébrica discreta para a Eq. (1) é dada por:
|
|
(19) |
onde,
|
|
(20) |
|
|
(21) |
|
|
(22) |
|
|
(23) |
|
|
(24) |
|
|
(25) |
Para integrar a Eq. (2) aplica-se o Teorema Fundamental do Cálculo considerando a formulação totalmente implícita. Deste modo, o lado esquerdo desta equação é reescrita em função das variáveis calculadas em e nas faces , conforme a expressão 26:
|
|
(26) |
Na expressão 26 o termo é escrito como onde é conhecido e é a variável ativa a ser calculada. A interpolação UDS é usada para avaliar , enquanto a interpolação CDS para avaliar nas faces. Por exemplo,
|
|
(27) |
com definido na equação (17). O termo quadrático da expressão (26) da variável secundária é calculado usando a interpolação CDS com os valores disponíveis da Eq. (19) e assim,
|
|
(28) |
A mesma abordagem é usada nos termos advectivos da expressão (26). O produto é dividido em com UDS para variável ativa e CDS para as variáveis secundárias, atualizada e . Para a integração do lado direito da Eq. (2), que representa a resistência à declividade, o valor de é calculada no centróide , pois fisicamente a fonte representa a média integral no volume discreto centrado em , isto é, o fonte não flui, é um termo volumétrico. Portanto, e a magnitude da velocidade é constante. Dessa forma, a integral do lado direito da Eq. (2) é reescrita da seguinte forma:
|
|
(29) |
onde os valores da variável principal nas faces são obtidos por UDS. Assim, a forma discreta linearizada da Eq. (2) é dada por:
|
|
(30) |
onde,
|
|
(31) |
|
|
(32) |
|
|
(33) |
|
|
(34) |
|
|
(35) |
|
|
(36) |
com
|
|
(37) |
A mesma abordagem é usada para o cálculo de , integrando a Eq. (3). Assim, são obtidos três sistemas lineares a serem resolvidos:
|
|
(38) |
onde representa a matriz de coeficientes da variável ( ou ), enquanto é o vetor que contém as condições de contorno e termos fontes.
3 O algoritmo
O código de simulação computacional foi programado em Linguagem Fortran, compilado na versão Fortran Power Station 4.0 licenciada pela Microsoft Corporation. A escolha por esse programa deve-se à sua velocidade de execução e alta capacidade de armazenamento de dados. Neste trabalho, o domínio físico retangular é dividido em e volumes de controle com comprimentos dados por nas direções e , respectivamente. Da mesma forma, o espaço temporal é dividido em passos de tempo uniformes iguais a . A malha cartesiana ordenada e estruturada é varrida de acordo com o par da esquerda para a direita aumentando o comprimento na direção , e de baixo para cima aumentando o comprimento na direção , começando no centróide que representa o ponto . Desta forma, faz-se a seguinte correspondência:,
|
|
(39) |
Após a discretização do domínio, são lidas a topografia da parte inferior, representada pela superfície , e as condições iniciais e . O sistema linear é resolvido por um método de Gauss-Seidel de acordo com a direção varrida anteriormente descrita. Ele itera até que um dos dois critérios seja atingido: o número máximo residual ou máximo de iterações . Se for atingido resíduo em um número de iterações e , então continua-se o processo iterativo até iterações. Ou seja, ao atingir a tolerância do resíduo máximo, faz-se mais iterações, isso torno o resíduo bem inferior ao residual máximo permitido. Para este trabalho, o número máximo de iterações para cada intervalo de tempo é fixado em iterações, enquanto a tolerância para o resíduo máximo global permitido é igual a , sendo o resíduo global definido como:
|
|
(40) |
onde é o número total de volume de controles, e os resíduos são a soma dos resíduos individuais de cada volume de controle,calculados incrementalmente de acordo com a Eq. (41):
|
|
(41) |
onde representa a diferença absoluta entre os dois lados da equação linearizada para a variável . O algoritmo completo é apresentado abaixo. O código também permite usar a última solução para inicializar uma nova execução com novas condições de contorno, se necessário.
|
Declare as matrizes principais e e as variáveis secundárias e Leia os dados do modelo: tamanho da malha espacial e temporal, coeficiente de atrito. Calcule o comprimento dos passos espaciais e temporal Faça a leitura da topografia Leia as condições iniciais e Calcule em cada passa de tempo as variáveis principais Se então Calcular as variáveis no contorno Se e então Interpolar e nos pontos de integração nas faces do volume de controle Calcular os coeficientes do sistema linear de Calcular o resíduo Se então Calcular Calcular a coluna de água Atualizar os valores de nas faces dos volumes de controle Calcular os coeficientes do sistema linear de Calcular o resíduo Calcular Atualizar os valores de nas faces dos volumes de controle Calcular os os coeficientes do sistema linear de Calcular o resíduo Calcular caso contrário Faça e iguais a zero (o nível da água é calculado até .) (fim da malha varrida) Teste de Convergência Atualização de e no tempo (fim do loop temporal) Faça o pós-processamento (tabelas e gráficos) |
4 Validação da solução numérica
Com o objetivo de validar a abordagem numérica apresentada na seção anterior, esta seção apresenta uma comparação com os resultados obtidos para um modelo de abertura instantânea de comportas apresentado em [10]. Este problema consiste em um domínio quadrado com de comprimento com uma barragem interna com de largura, disposta na faixa de , que divide o domínio como é mostrado na Fig. (2) . Para simulação da abertura de comportas, considera-se uma abertura não simétrica e instantânea com de largura entre e . Essa abertura causa uma liberação sutil da coluna de água a jusante, resultando em um fluxo com gradientes espaciais e temporais acentuados.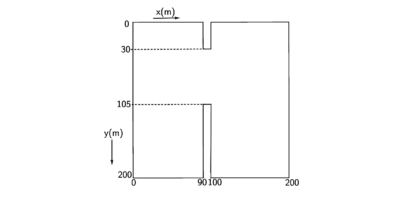
|
| Figure 2: Domínio do modelo |
Todos os parâmetros numéricos e físicos são mostrados na Tabela (1). De acordo com [10], neste problema a resistência ao escoamento é desprezada e sua parte inferior é plana.
| Tamanho da malha | Tamanho dos elementos | Passo de tempo | Coeficiente de Manning | ||
4.1 Condições Iniciais
Para o tempo inicial, o fluido é quiescente, ou seja, para todo o domínio, enquanto a coluna d'água inicial é dada por:
|
|
(42) |
com o nível da água à montante e a jusante . Consequentemente, a razão entre os níveis de água é
4.2 Condições de Contorno
Por uma questão de clareza, esta seção é apresentada aqui para mostrar de forma prática como as condições de contorno são tratadas neste trabalho usando para isso, o caso de validação como exemplo. As abordagens apresentadas aqui também são aplicadas a outros casos de maneira similar, respeitando, é claro, a configuração geométrica de cada um. Como abordagem teórica, existem pelo menos três maneiras de lidar com as condições de contorno: realizar um balanço para cada volume de controle na fronteira, chamado simplesmente de equilíbrio de contorno; considerar um meio volume na fronteira com seu centróide pertencente ao próprio limite; e, por último, considerar volumes fictícios em torno dos limites, isso significa que o valor de limite prescrito deve ser igual à interpolação (qualquer que seja) entre os centróides do volume real de controle e o novo volume de controle fictício. Esta última abordagem é preferida, pois a primeira implica um tratamento matemático distinto para cada fronteira, o que torna o código mais complexo de acordo com a geometria. O caminho de ordem, o meio volume, não é conservador porque o valor é imposto, em vez disso, como resultado de um balanço de fluxo. A abordagem de volume fictício permite que toda a malha seja constituída por volumes inteiros, o que é fácil de codificar e tem a mesma natureza conservadora para todos os volumes. Embora este artifício aumente o número de incógnitas do problema, acarretando custo computacional, é um procedimento útil com codificação fácil. Na Fig. (3) é apresentado um esboço deste conceito.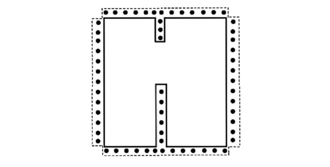
|
| Figure 3: Volumes fictícios ao redor da malha real |
Utiliza-se a Condição de Neumann nula para o nível da água nas paredes externas e nos contornos da represa. Desse modo,
|
|
(43) |
|
|
(44) |
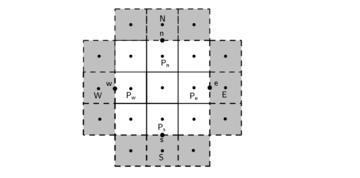
|
| Figure 4: Esquema da condição de contorno para o nível do fluido |
Todas as derivadas nas faces fronteiras ( e ) podem ser interpoladas como funções dos centróides vizinhos destacados na Fig. 4: um externo fictício ( ou ) e um interno pertencente ao domínio. Consequentemente,
|
|
(45) |
|
|
(46) |
|
|
(47) |
|
|
(48) |
o que resulta em,
|
|
(49) |
Para as variáveis de fluxo ( e ), as paredes são consideradas impermeáveis e todas as componentes de velocidade normal aos contornos são nulas. Esta condição de Dirichlet é imposta considerando o esquema de diferenciação central, ou seja,
|
|
(50) |
|
|
(51) |
|
|
(52) |
|
|
(53) |
e portanto,
|
|
(54) |
|
|
(55) |
Por outro lado, as componentes da velocidade tangencial são calculados considerando derivada nula para cada uma, ou seja, uma Condição de Neumann nula para cada componente tangencial, e então
|
|
(56) |
|
|
(57) |
|
|
(58) |
|
|
(59) |
e portanto,
|
|
(60) |
|
|
(61) |
4.3 Resultados
O algoritmo proposto e a formulação numérica devem ser validados para determinar sua precisão e robustez. Isso é feito por meio da aplicação do modelo e do código numérico a um problema representativo de águas rasas: o problema da abertura instantânea de comportas, amplamente utilizado para testar códigos numéricos ou modelos matemáticos que tratam de vazões superficiais sujeitas a mudanças abruptas, mudanças no tempo e no espaço, e a abertura instantânea de comportas tem esses detalhes físicos e é amplamente estudada na literatura [10,11,21,22,23].
4.3.1 Nível da água
A Fig. (5) mostra a superfície livre de água após segundos após a abertura da comporta. Os resultados são comparados com aqueles obtidos em [10]. Observa-se na Fig. (5) uma frente de onda após a abertura da eclusa e uma onda de depressão no lado esquerdo à barreira. Os níveis de superfície computados estão de acordo com os apresentados por [10] para o mesmo instante de tempo.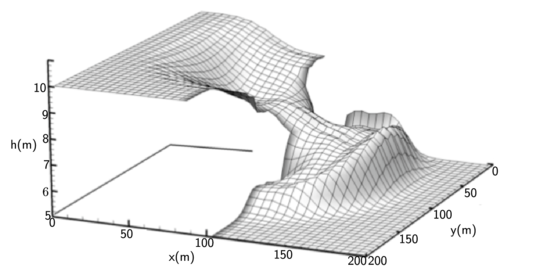
|
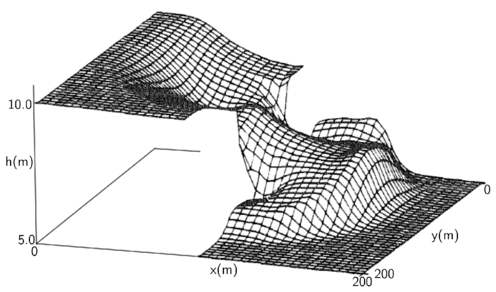 ] ]
|
| (a) Resultado obtido pelo esquema híbrido proposto | (b) Resultado obtido em [10] |
| Figure 5: Comparação do comportamento da superfície livre após após a abertura da comporta | |
A Tabela (4.3.1) mostra os valores de nível para algumas posições do domínio para fins de comparação quantitativa.
| yx | |||||||||
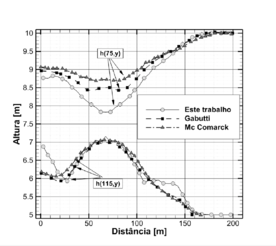
|
| Figure 6: Comparação do perfil do nível de água em duas linhas de amostra em e |
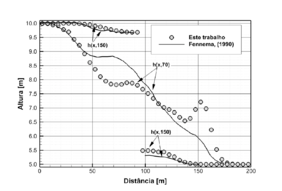
|
| Figure 7: Comparação das linhas de amostra longitudinais do nível de água em e |
|
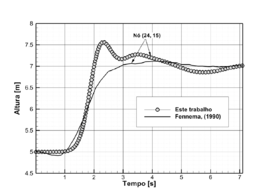
| Figure 8: Comparação do tempo de amostragem do nível da água em |
Pode ser visto em ambos os resultados que a frente de onda leva segundo após a abertura para alcançar o ponto de teste , e depois de segundos, o nível da água está próximo de em ambos os casos. Novamente, há um comportamento mais dinâmico em comparação com os resultados de [10], que é mais suave com oscilações brandas devido a utilização de termos dissipativos artificiais, enquanto os resultados obtidos pelo esquema híbrido proposto apresentam uma onda de pico que tende a ser atenuada com o tempo, de acordo com o fenômeno físico esperado.
4.3.2 Campo de Velocidade
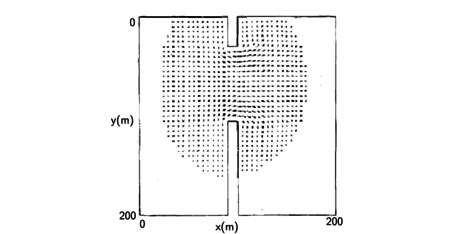
A Fig. (9) compara os resultados de [10] e deste trabalho para o campo de velocidade no instante de tempo igual a segundos. Os vetores do campo de velocidade estão em muito boa concordância apresentando as mesmas direções, magnitudes (representadas pelos tamanhos das flechas) com um espalhamento pela mesma área ao redor da abertura da comporta.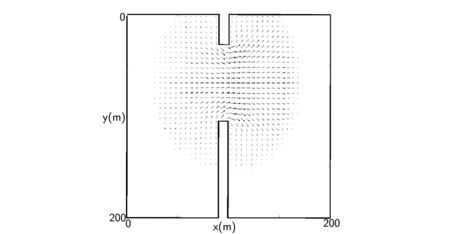
|
 ] ]
|
| (a) Campo de velocidade usando o esquema híbrido | (b) Campo de velocidade apresentado em [10] |
| Figure 9: Comparação do campo de velocidade em torno da abertura da comporta em segundos | |
4.4 Considerações
Apesar das oscilações locais ou da suavidade, os resultados estão em boa concordância geral com as frentes de onda e ondas de depressão de acordo com os dados da literatura, o que reflete a habilidade da abordagem numérica proposta em lidar e capturar o comportamento físico do fluxos de águas rasas que validam o modelo e a abordagem numérica. É importante enfatizar que, em [10] artifícios numéricos foram usados como uma viscosidade artificial para lidar com as oscilações da superfície livre, o que torna o resultado de [10] mais difusivo e quase sem flutuações locais no nível da superfície. Por outro lado, neste trabalho, nenhuma abordagem similar foi empregada para lidar com uma possível instabilidade numérica devido à aproximação de tempo de alta ordem. O esquema de tempo implícito proposto de ordem neste trabalho mostrou-se capaz de capturar o comportamento físico e os gradientes de tempo rígidos sem etapas de tempo proibitivas. E a formulação UDS em associação com a abordagem CDS foi capaz de lidar com mudanças abruptas nos campos de variáveis sem instabilidades ou oscilações não físicas. Todas as oscilações de superfície livre têm um significado físico quando as diferenças de velocidade entre as porções distintas da onda são contabilizadas porque essas diferenças compactam a onda e aumentam sua amplitude. Como apontado em [10], as oscilações numéricas puras não são amortecidas com o tempo, em vez disso, elas tendem a ser amplificadas com gradientes rígidos, o que faz com que o sistema divirja. Porém fazendo uso do esquema numérico híbrido aqui apresentado, a solução se mantêm suave com resíduos muito baixo, inferiores a tolerância máxima de . Mesmo para grandes intervalos de tempo, não há crescimento no valor destes resíduos, atingindo valores inferiores a tolerância máxima em poucas iterações.
5 Verificação Numérica
Uma validação numérica assegura que o modelo é capaz de fornecer uma resposta física correta sob certas condições iniciais e de contorno. No entanto, mais testes são feitos para descobrir se, sob outro cenário, o modelo computacional é capaz de prever o comportamento físico do sistema. Esta etapa, juntamente com a validação anterior, permite definir se o modelo computacional é útil como uma ferramenta preditiva para qualquer fluxo de água superficial sob condições diversas.
5.1 Teste da condição de leito seco
Para avaliar a robustez do código, o modelo da seção 3 é considerado, fazendo a razão tender a zero, isto é, é considerado com uma fina película líquida, como uma “wet condition”. Esta situação é geralmente uma situação física difícil de resolver devido às singularidades que podem surgir nos termos fontes de atrito, e o possível mau condicionamento da matriz de coeficientes devido a valores nulos que surgirão ao longo dos cálculos quando tende a zero. Nesta situação, as equações de águas rasas tendem a enfraquecer seu significado físico. Em vista disso, não pode ser exatamente zero, e o código deve ser capaz de lidar com essa situação. Na Fig.(10), pode-se observar o nível da água para os primeiros segundos com .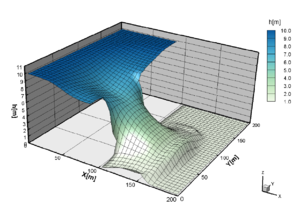
|
| Figure 10: Visão tridimensional da superfície livre em segundos após a abertura da comporta com |
Os valores dos níveis são reproduzidos na Tabela 3, com todas as unidades em metros.
| yx | |||||||||
5.2 Considerações
Em [10], [15] e [13] são apontadas as dificuldades em lidar com modelo que representam leitos quase secos, devido as possíveis singularidades. O esquema numérico híbrido CDS/UDS aqui proposto mostrou-se eficaz e com baixo custo computacional para simular escoamentos transientes em águas rasas para leitos quase secos, o que evidencia a acurácia e robustez do esquema.
6 Escoamento em um reservatório de contenção subterrâneo: uma aplicação do modelo completo
Os reservatórios subterrâneos são projetados para zonas urbanas populosas, onde não há lugar para armazenar água da chuva. Eles são construídos com uma rede de pilares de sustentação e canais de drenagem na parte inferior, como ilustrado na Fig. (11)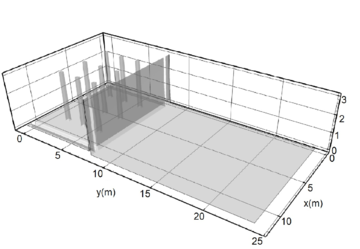
|
| Figure 11: Reservatório de águas pluviais subterrâneas |
|
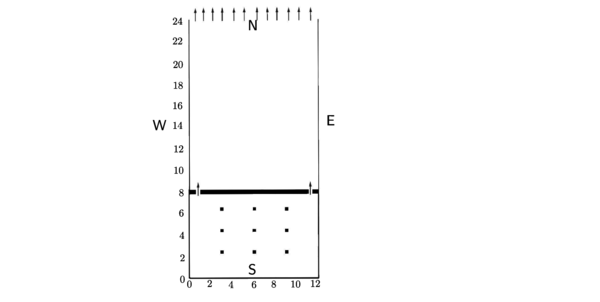
| Figure 12: Domínio físico do reservatório subterrâneo |
|
|
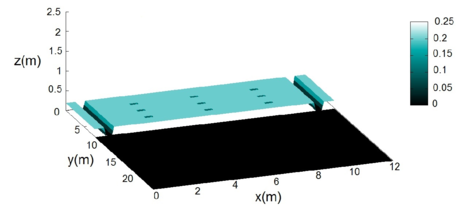
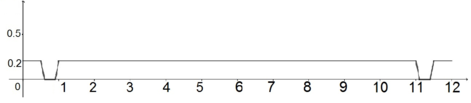
| (a) representação tridimensional do fundo | (b) Perfil frontal do fundo do reservatório |
| Figure 13: Topografia do fundo do reservatório | |
As configurações da topografia do fundo são descritas por na Eq.(62).
|
|
(62) |

|
| Figure 14: Condições iniciais para o nível da água |
Com relação aos componentes de velocidade, é necessário dizer que: como as paredes do reservatório, os pilares e paredes laterais do domínio externo são considerados impermeáveis; o fluxo da água que é armazenada no reservatório ocorre apenas nas saídas da parede norte do reservatório e na extremidade norte do domínio externo, como indicado na Fig. (12). Mais precisamente, a componente de velocidade nas paredes internas leste-oeste e nos contornos internos é nula, enquanto a componente de velocidade é considerada nula no limite sul e nos limites internos norte-sul. Por outro lado, nos contornos norte-sul para a componente e nos contornos leste-oeste para o componente respectivamente, é adotada a condição de Neumann nula, como na Seção 4. Para o domínio externo, uma vez que existem apenas paredes laterais, o fluxo é livre para todos os pontos da extremidade norte. Essa condição de contorno é descrita pelas expressões:
|
|
(63) |
|
|
(64) |
sendo um coeficiente arbitrário, o nível da água e a aceleração da gravidade. Para a simulação computacional do modelo proposto utilizamos uma malha estruturada, de espaçamento no espaço bidimensional, com intervalo de tempo de . Como há uma topografia especificada na parte inferior do reservatório, é necessário estabelecer uma condição compatível com a física do modelo: se o nível da água atingir o fundo do reservatório, o fluxo será considerado nulo neste ponto. Mais precisamente se, os cálculos para são feitos para o próximo passo de tempo, caso contrário faz-se: e as componentes de velocidade são anuladas neste ponto. O volume de fluido armazenado no interior do reservatório foi calculado em cada ponto de tempo. E foi estabelecido como critério de parada no código, o volume mínimo
6.1 Resultados
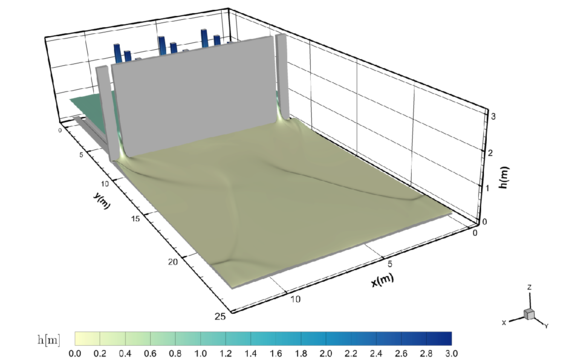
Devido às aberturas na parede norte do reservatório, há um declínio no nível da água dentro do reservatório e ondas de elevação no domínio externo, especialmente nas proximidades das aberturas. A Fig. (15) é uma representação em perspectiva da superfície da água em todo o domínio para e após a abertura das saídas.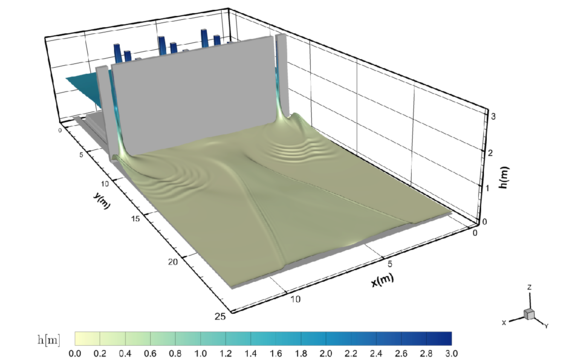
|
|
| (a) | (b) |
| Figure 15: Visão tridimensional do nível da água após o início do despejo | |
|
|
| (a) | (b) |

|
|
| (c) | (d) |
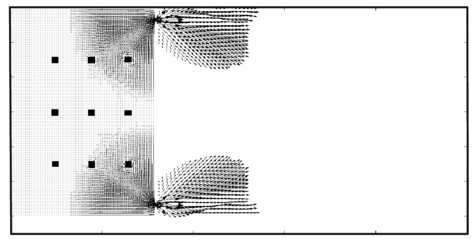
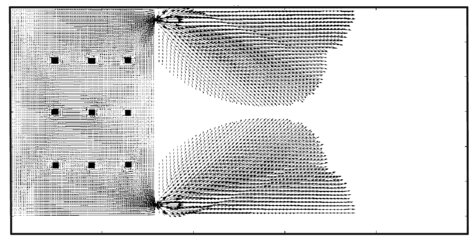
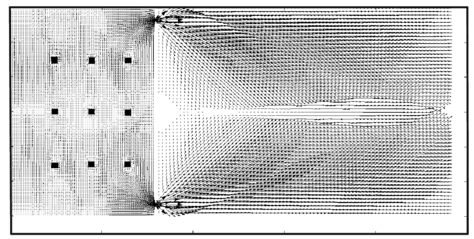
| Figure 16: Campo de velocidade nos primeiros segundos | |

|
|
| (a) | (b) |
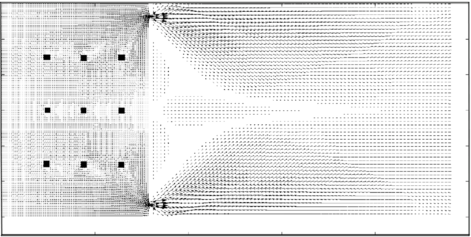
| Figure 17: Campo de velocidade após o início do despejo | |
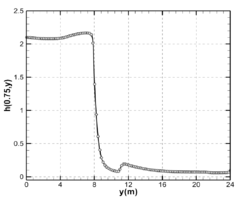
|
| Figure 18: Perfil do nível de água em uma linha de amostra em para |
O código implementado foi utilizado para análises como: variação de volume no reservatório em função do tempo, o comportamento do fluxo ao redor dos pilares e na vizinhança das paredes. Em todas essas análises, os resultados obtidos são satisfatórios e consistentes com a física do problema.
7 Conclusões
Foi proposto um método de volume finito implícito de ordem com uma discretização híbrida CDS/UDS para resolver as equações completas de águas rasas. O algoritmo mostrou-se capaz de lidar com fortes problemas instáveis como a abertura instantânea de comportas, vazão em topografias não uniformes com condição dry/wet, com e sem condições de saídas. Os resultados mostram boa concordância com a literatura com dinâmica de frente de onda mais complexa. Essas diferenças locais são explicadas devido à ausência de artifício numérico, como a viscosidade artificial, que amortece o comportamento da superfície livre e suaviza as ondas. A formulação numérica proposta tem a vantagem de ser mais fácil de codificar em comparação com aquelas disponíveis na literatura e, além disso, o apelo físico para a conservação de fluxo que é característica do método de volumes finitos, torna-se uma opção com a mesma precisão física, porém simples e rápida para ser implementada. A convergência do método iterativo de Gauss-Seidel, mesmo impondo máximo residual muito pequeno, é obtida com poucas iterações, o que garante baixo custo computacional. Como ferramenta preditiva, o modelo computacional tem mostrado bons resultados desde a configuração simples até a mais complexa, com precisão e robustez. A solução numérica obtida pode ser usada para simular fluxos sobre topografias reais encontradas na natureza.
8 Declaração de disponibilidade de dados
Todos os dados, modelos ou códigos gerados ou utilizados durante o estudo estão disponíveis pelo autor correspondente por solicitação. Lista de itens:
- o algoritmo utilizado para obtenção da solução numérica híbrida proposta;
- o arquivo de dados da Tabela 2;
- o arquivo de dados da Tabela 3;
- os dados usados para gerar as figuras.
Agradecimentos
Este estudo foi financiado em parte pela Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001. Os autores agradecem também ao Departamento de Matemática da Universidade Tecnológica Federal do Paraná (UTFPR), Campus Campo Mourão e ao Programa de Pós-Graduação em Métodos Numéricos (PPGMNE) da Universidade Federal do Paraná (UFPR).
9 Referências
[1] Imbonden, D. M. (2004) "The Lakes Handbook, Limmnology and Limnectic Ecology". Blackwell Scienc Ltd
[2] Reynolds, C. (1984) "The ecology of freshwater phytoplankton". Cambridge University Press
[3] Mahmood, K. and Yevjevich, V. (1975) "Unsteady flow in open channels". Water Resources Publications, 1 th Edition
[4] Vreugdenhil, C. B. (1994) "Numerical Methods for Shallow-Water flow". Springer Science+Business Media Dordrecht
[5] García-Navarro, P. and Alcrudo, F. and Priestley, A. (1994) "An implicit method for water flow modelling in channels and pipes", Volume 32. J. Hydraul. Eng. 721–742
[6] Burguete, J. and García-Navarro, P. (2004) "Implicit schemes with large time step for non-linear equations: Application to river flow hydraulic", Volume 46. Internat. J. Numer. Methods Fluids 607–636
[7] Cantero-Chinchilla, F. N. and Castro-Orgaz, O. and Dey, S. and Ayuso, J. L. (2016) "Nonhydrostatic Dam Break Flows. I: Physical Equations and Numerical Schemes", Volume 142. J. Hydraul. Eng. 12 1–19
[8] Soler, J., Bladé, E., Sánchez-Juny, M. (2012) "Ensayo comparativo entre modelos unidimensionales y bidimensionales en la modelización de la rotura de una balsa de materiales sueltos erosionables", Volume 28 (2). Revista International de Métodos Numéricos para Cálculo y Diseño en Ing. 103–105
[9] Brufau, P., García-Navarro, P., (2000) "Esquemas de alta resolución para resolver las ecuaciones de "shallow water"", Volume 16 (4). Revista International de Métodos Numéricos para Cálculo y Diseño en Ing. 493–512
[10] Fennema, R. J. and Chaudhry, M.H. (1990) "Explicit Methods for 2-D transient free surface flows", Volume 116. J. Hydraul. Eng. 8 1013–1034
[11] Nikolos, I.K. and Delis, A.I. (2009) "An unstructured node-centered finite volume scheme for shallow water flows with wet/dry fronts over complex topography", Volume 198. Comput. Methods. Appl. Mech. Engrg 3723–3750
[12] Valiani, A. and Caleffi, V. and Zanni, A. (2002) "Case Study: Malpasset Dam-Break Simulation using a Two-Dimensional Finite Volume Method", Volume 128. J. Hydraul. Eng. 5 460–472
[13] Fernández-Pato, J. and Morales-Hernández, M. and García-Navarro, P. (2018) "Implicit finite volume simulation of 2D shallow water flows in flexible meshes", Volume 328. Comput. Methods. Appl. Mech. Engrg 1–25
[14] Melo, A. R., Gramani, L. M., Kaviski, E. (2018) "High-order CE/SE scheme for dam-break flow simulation", Volume 34 (1). Revista International de Métodos Numéricos para Cálculo y Diseño en Ing. 1–12
[15] Sheu, T. W. H. and Fang, C. C. (2001) "High resolution finite-element analysis of shallow water equations in two dimensions", Volume 190. Comput. Methods. Appl. Mech. Engrg 2581–2601
[16] Villota, A., Codina, R. (2018) "Approximation of the shallow water equations with higher order finite elements and variational multiscale methods", Volume 34 (1). Revista International de Métodos Numéricos para Cálculo y Diseño en Ing. 1–25
[17] Hirsch, J. J. (2007) "Water Waves: The Mathematical Theory with Applications", Volume. Interscience Publishers, Edition
[18] Blazek, J. (2001) "Computational fluid dynamics: principles and applications.". Elsevier Science Ltd, 1 th Edition
[19] Versteeg, H.K. and Malalasekera, W. (2007) "An Introduction to Computational Fluid Dynamics. The finite volume method". Pearson Education Limited, 2 th Edition
[20] Maliska, C. R. (2013) "Transferência de Calor e Mecânica dos Fluidos Computacional". LTC, 2 th Edition
[21] Patankar, S. (1980) "Numerical heat transfer and fluid flow". Hemisphere Publishing Corporation, Edition
[22] MacCormack, R. W. (1969) "The effect of viscosity in hypervelocity impact cratering", Volume. American Institutue Aeronautics Astronautics 69–354
[23] Gabutti, B. (1983) "On two upwind finite-difference schemes for hyperbolic equations in non-conservative form", Volume 11. Comput. Fluids 3 207–230
[24] Porto, R. M. (2006) "Hidráulica Básica". EESC-USP, 4 th Edition
Document information
Published on 02/04/20
Accepted on 30/03/20
Submitted on 20/08/19
Volume 36, Issue 2, 2020
DOI: 10.23967/j.rimni.2020.03.007
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?