| (22 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | Published in ''Computational Mechanics'' (2015). Vol. 55, pp. 1091–1104 <br /> | ||
| + | doi: 10.1007/s00466-014-1107-0 | ||
==Abstract== | ==Abstract== | ||
| Line 87: | Line 89: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\displaystyle \rho \frac{D ( {\mathbf{V}} )}{D t} = \nabla \sigma + \rho \mathbf{g} \qquad \hbox{in} \Omega </math> | + | | style="text-align: center;" | <math>\displaystyle \rho \frac{D ( {\mathbf{V}} )}{D t} = \nabla \sigma + \rho \mathbf{g} \qquad \hbox{in } \Omega </math> |
| style="width: 5px;text-align: right;white-space: nowrap;" | (2.a) | | style="width: 5px;text-align: right;white-space: nowrap;" | (2.a) | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> \displaystyle \frac{D p}{D t} + \kappa \nabla . {\mathbf{V}} = 0 \qquad \quad \hbox{in} \Omega </math> | + | | style="text-align: center;" | <math> \displaystyle \frac{D p}{D t} + \kappa \nabla . {\mathbf{V}} = 0 \qquad \quad \hbox{in } \Omega </math> |
| style="width: 5px;text-align: right;white-space: nowrap;" | (2.b) | | style="width: 5px;text-align: right;white-space: nowrap;" | (2.b) | ||
|} | |} | ||
| Line 367: | Line 369: | ||
| style="text-align: center;" | <math>\begin{bmatrix}{\mathbf{K}}(\mu )+ \frac{{\mathbf{M}}(\rho )}{\Delta t} & {\mathbf{G}}\\ {\mathbf{G}}^T & 0 \end{bmatrix} \begin{bmatrix}{\mathbf{\bar V}}^{n+1} \\ \bar p^{n+1} \end{bmatrix} = \begin{bmatrix}\frac{1}{\Delta t}{\mathbf{M \bar V}}^n + \mathbf{Mg} \\ 0 \end{bmatrix} </math> | | style="text-align: center;" | <math>\begin{bmatrix}{\mathbf{K}}(\mu )+ \frac{{\mathbf{M}}(\rho )}{\Delta t} & {\mathbf{G}}\\ {\mathbf{G}}^T & 0 \end{bmatrix} \begin{bmatrix}{\mathbf{\bar V}}^{n+1} \\ \bar p^{n+1} \end{bmatrix} = \begin{bmatrix}\frac{1}{\Delta t}{\mathbf{M \bar V}}^n + \mathbf{Mg} \\ 0 \end{bmatrix} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (19) |
|} | |} | ||
| − | In | + | In Eq. [[#eq-19|(19)]], first order finite differences are used in the acceleration term to advance in time and <math display="inline"> {\bar{(\cdot )}} </math> denotes nodal variables. The sub-matrices of the system are the standard ones obtained after using the Galerkin FEM for fluid problems <span id='citeF-8'></span>[[#cite-8|[8]]]. |
===3.2 Stabilized matrix form for the fluid phase=== | ===3.2 Stabilized matrix form for the fluid phase=== | ||
| Line 378: | Line 380: | ||
In order to overcome this limitation, stabilization terms can be added to the set of equations [[#eq-19|(19)]]. As stated before, it is necessary to stabilize the pressure equation for the fluid problem only. While there are several methods to do so, only two will be mentioned in this work: the Pressure-Stabilizing/Petrov-Galerkin (PSPG) method <span id='citeF-10'></span>[[#cite-10|[10]]] and the Orthogonal Subgrid Scale (OSS) stabilization <span id='citeF-11'></span>[[#cite-11|[11]]]. The reason behind this is that both methods add a Laplacian to the LHS of the system of equations [[#eq-19|(19)]], thus preserving the symmetry of the system. | In order to overcome this limitation, stabilization terms can be added to the set of equations [[#eq-19|(19)]]. As stated before, it is necessary to stabilize the pressure equation for the fluid problem only. While there are several methods to do so, only two will be mentioned in this work: the Pressure-Stabilizing/Petrov-Galerkin (PSPG) method <span id='citeF-10'></span>[[#cite-10|[10]]] and the Orthogonal Subgrid Scale (OSS) stabilization <span id='citeF-11'></span>[[#cite-11|[11]]]. The reason behind this is that both methods add a Laplacian to the LHS of the system of equations [[#eq-19|(19)]], thus preserving the symmetry of the system. | ||
| − | In | + | In Eq. [[#eq-20|(20)]] the final matrix system is presented for the PSPG method. Using the OSS method with an explicit projection stage would lead to a similar expression but with the explicit projection of the pressure in the RHS. |
| − | <span id="eq- | + | <span id="eq-20"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 388: | Line 390: | ||
| style="text-align: center;" | <math>\begin{bmatrix}{\mathbf{K}}(\mu )+ \frac{1}{\Delta t} {\mathbf{M}}(\rho ) & {\mathbf{G}}\\ {\mathbf{G}}^T & \tau L(\frac{1}{\rho }) \end{bmatrix} \begin{bmatrix}{\mathbf{\bar V}}^{n+1} \\ \bar p^{n+1} \end{bmatrix} = \begin{bmatrix}\frac{1}{\Delta t}{\mathbf{M \bar V}}^n + \mathbf{Mg} \\ \tau {\mathbf{G}}^T \mathbf{g} \end{bmatrix} </math> | | style="text-align: center;" | <math>\begin{bmatrix}{\mathbf{K}}(\mu )+ \frac{1}{\Delta t} {\mathbf{M}}(\rho ) & {\mathbf{G}}\\ {\mathbf{G}}^T & \tau L(\frac{1}{\rho }) \end{bmatrix} \begin{bmatrix}{\mathbf{\bar V}}^{n+1} \\ \bar p^{n+1} \end{bmatrix} = \begin{bmatrix}\frac{1}{\Delta t}{\mathbf{M \bar V}}^n + \mathbf{Mg} \\ \tau {\mathbf{G}}^T \mathbf{g} \end{bmatrix} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (20) |
|} | |} | ||
In Equations [[#eq-23|(23)]], <math display="inline">\mathbf{L}(\frac{1}{\rho })</math> is the Laplacian of the pressure. Another alternative to stabilize the equations is the Finite Increment Calculus (FIC) procedure <span id='citeF-6'></span>[[#cite-6|[6]]].The FIC method avoids the need to prescribe the pressure in free surface solvers using staggered schemes. A mixed FEM Lagrangian formulation for treating both quasi and fully incompressible fluids as well as FSI problems using the FIC method is presented in <span id='citeF-6'></span>[[#cite-6|[6]]]. | In Equations [[#eq-23|(23)]], <math display="inline">\mathbf{L}(\frac{1}{\rho })</math> is the Laplacian of the pressure. Another alternative to stabilize the equations is the Finite Increment Calculus (FIC) procedure <span id='citeF-6'></span>[[#cite-6|[6]]].The FIC method avoids the need to prescribe the pressure in free surface solvers using staggered schemes. A mixed FEM Lagrangian formulation for treating both quasi and fully incompressible fluids as well as FSI problems using the FIC method is presented in <span id='citeF-6'></span>[[#cite-6|[6]]]. | ||
| − | The system [[#eq- | + | The system [[#eq-20|(20)]] can be solved by choosing an appropriate stabilization parameter <math display="inline">\tau </math>. In this work <math display="inline">\tau ={\left(1/ \Delta t + 4 \mu / h^2 + 2 V^n / h \right)} ^{-1} </math> following the work in <span id='citeF-12'></span>[[#cite-12|[12]]]<span id='citeF-10'></span>[[#cite-10|[10]]]. The dependency on <math display="inline">\Delta t</math> was added to avoid <math display="inline">\tau \rightarrow \infty </math> when the velocity and the viscosity are zero <span id='citeF-10'></span>[[#cite-10|[10]]]. |
===3.3 Matrix form for the solid phase=== | ===3.3 Matrix form for the solid phase=== | ||
| Line 399: | Line 401: | ||
Unlike fluids, solids will not be considered incompressible. The spatial discretization and variables will be the same as for the fluids formulation: linear elements for both the pressure and the velocity. As for the deviatoric stress, it will not be an independent variable, but a state variable depending on the velocity unknowns. | Unlike fluids, solids will not be considered incompressible. The spatial discretization and variables will be the same as for the fluids formulation: linear elements for both the pressure and the velocity. As for the deviatoric stress, it will not be an independent variable, but a state variable depending on the velocity unknowns. | ||
| − | Recalling the general system of | + | Recalling the general system of Eqs. [[#2.2 Continuum equations|(2)]] and splitting the stresses into its deviatoric and volumetric components, the system of governing equations reads: |
| − | <span id="eq- | + | <span id="eq-21"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 407: | Line 409: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\rho \frac{D ( {\mathbf{V}} )}{D t} = \nabla \left(\sigma ' - p \mathbf{I} \right)+ \rho \mathbf{g} \qquad \hbox{in} \Omega </math> | + | | style="text-align: center;" | <math>\rho \frac{D ( {\mathbf{V}} )}{D t} = \nabla \left(\sigma ' - p \mathbf{I} \right)+ \rho \mathbf{g} \qquad \hbox{in } \Omega </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (21) |
|- | |- | ||
| − | | style="text-align: center;" | <math> \frac{D p}{D t} + \kappa \nabla . {\mathbf{V}} = 0 \qquad \hbox{in} \Omega </math> | + | | style="text-align: center;" | <math> \frac{D p}{D t} + \kappa \nabla . {\mathbf{V}} = 0 \qquad \hbox{in } \Omega </math> |
|} | |} | ||
|} | |} | ||
| Line 416: | Line 418: | ||
The weak form of the problem is | The weak form of the problem is | ||
| − | <span id="eq- | + | <span id="eq-22"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 422: | Line 424: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\left(\mathbf{w} , \rho \frac{D ( {\mathbf{V}} )}{D t} \right)_ \Omega = - \left(\nabla \mathbf{w} , \sigma ' - p \mathbf{I} \right)_ \Omega | + | | style="text-align: center;" | <math>\left(\mathbf{w} , \rho \frac{D ( {\mathbf{V}} )}{D t} \right)_ \Omega = - \left(\nabla \mathbf{w} , \sigma ' - p \mathbf{I} \right)_ \Omega + \left(\mathbf{w} , \rho \mathbf{g} \right)_ \Omega + \left(\mathbf{w} , \mathbf{t}^p \right)_ {\Gamma _t} </math> |
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| style="text-align: center;" | <math> \left(q , \frac{D p}{D t} + \kappa \nabla . {\mathbf{V}} \right)_ \Omega = 0 </math> | | style="text-align: center;" | <math> \left(q , \frac{D p}{D t} + \kappa \nabla . {\mathbf{V}} \right)_ \Omega = 0 </math> | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (22) | ||
|} | |} | ||
|} | |} | ||
| Line 444: | Line 444: | ||
Using finite differences in time for the pressure, dividing the second equation by the compressibility modulus <math display="inline">\kappa </math> and recalling the definition of the stresses [[#eq-15|(15)]] yields: | Using finite differences in time for the pressure, dividing the second equation by the compressibility modulus <math display="inline">\kappa </math> and recalling the definition of the stresses [[#eq-15|(15)]] yields: | ||
| − | <span id="eq- | + | <span id="eq-23"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 456: | Line 456: | ||
| style="text-align: center;" | <math> \qquad \qquad \qquad \quad \left(q , \frac{p^{n+1}}{\kappa \Delta t} + \nabla . {\mathbf{V}} \right)_{\Omega } = \left(q , \frac{p^{n}}{\kappa \Delta t} \right)_{\Omega } </math> | | style="text-align: center;" | <math> \qquad \qquad \qquad \quad \left(q , \frac{p^{n+1}}{\kappa \Delta t} + \nabla . {\mathbf{V}} \right)_{\Omega } = \left(q , \frac{p^{n}}{\kappa \Delta t} \right)_{\Omega } </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (23) |
|} | |} | ||
The rate of defomations is calculated implicitly to avoid instabilities as | The rate of defomations is calculated implicitly to avoid instabilities as | ||
| − | <span id="eq- | + | <span id="eq-24"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 469: | Line 469: | ||
| style="text-align: center;" | <math>\qquad \qquad \mathbf{d} = \mathbf{B} \mathbf{V}^{n+1} </math> | | style="text-align: center;" | <math>\qquad \qquad \mathbf{d} = \mathbf{B} \mathbf{V}^{n+1} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (24) |
|} | |} | ||
| − | where <math display="inline">\mathbf{B}</math> is the standard strain-rate velocity matrix [[#eq- | + | where <math display="inline">\mathbf{B}</math> is the standard strain-rate velocity matrix [[#eq-27|(27)]]. Finally, writing the equations in matrix form, the system can be expressed as: |
| − | <span id="eq- | + | <span id="eq-25"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 482: | Line 482: | ||
| style="text-align: center;" | <math>\begin{bmatrix}\left(\frac{2}{\Delta t} \mathbf{M}(\rho ) + \Delta t \mathbf{K} \right) & \mathbf{G} \\ \mathbf{G}^T & \frac{1}{\Delta t} \mathbf{M}(\frac{1}{\kappa }) \end{bmatrix} \begin{bmatrix}\mathbf{\bar V}^{n+1} \\ \bar p^{n+1} \end{bmatrix} = </math> | | style="text-align: center;" | <math>\begin{bmatrix}\left(\frac{2}{\Delta t} \mathbf{M}(\rho ) + \Delta t \mathbf{K} \right) & \mathbf{G} \\ \mathbf{G}^T & \frac{1}{\Delta t} \mathbf{M}(\frac{1}{\kappa }) \end{bmatrix} \begin{bmatrix}\mathbf{\bar V}^{n+1} \\ \bar p^{n+1} \end{bmatrix} = </math> | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: center;" | <math> \begin{bmatrix}\mathbf{M}(\rho ) ( \frac{2}{\Delta t} \mathbf{\bar V}^{n} - \mathbf{ \bar {\dot V}}^{n} + \mathbf{g} )+ \mathbf{G} {\sigma '}^n_{n+1} \\ \frac{1}{\Delta t} \mathbf{M}(\frac{1}{\kappa }) \bar p^n \end{bmatrix} </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (25) |
|} | |} | ||
In general all the matrices have the same form used for the fluid elements, except for the stiffness matrix <math display="inline">\mathbf{K}</math>. Its expression is: | In general all the matrices have the same form used for the fluid elements, except for the stiffness matrix <math display="inline">\mathbf{K}</math>. Its expression is: | ||
| − | <span id="eq- | + | <span id="eq-26"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 497: | Line 497: | ||
| style="text-align: center;" | <math>\qquad \qquad \mathbf{K} = \int _{\Omega } \mathbf{B^T C' B} </math> | | style="text-align: center;" | <math>\qquad \qquad \mathbf{K} = \int _{\Omega } \mathbf{B^T C' B} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (26) |
|} | |} | ||
where <math display="inline">\mathbf{C'}</math> is the constitutive matrix for the deviatoric stresses. The expressions for <math display="inline">\mathbf{B}</math> and <math display="inline">\mathbf{C'}</math> for 3D problems are | where <math display="inline">\mathbf{C'}</math> is the constitutive matrix for the deviatoric stresses. The expressions for <math display="inline">\mathbf{B}</math> and <math display="inline">\mathbf{C'}</math> for 3D problems are | ||
| − | <span id="eq- | + | <span id="eq-27"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 508: | Line 508: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\mathbf{B} = \begin{bmatrix}\frac{\partial N}{\partial x} & 0 & 0 \\ 0 & \frac{\partial N}{\partial y} & 0 \\ 0 & 0 & \frac{\partial N}{\partial z} \\ \frac{\partial N}{\partial y} & \frac{\partial N}{\partial x} & 0 \\ 0 & \frac{\partial N}{\partial z} & \frac{\partial N}{\partial y} \\ \frac{\partial N}{\partial z} & 0 & \frac{\partial N}{\partial x} \end{bmatrix} | + | | style="text-align: center;" | <math>\mathbf{B} = \begin{bmatrix}\frac{\partial N}{\partial x} & 0 & 0 \\ 0 & \frac{\partial N}{\partial y} & 0 \\ 0 & 0 & \frac{\partial N}{\partial z} \\ \frac{\partial N}{\partial y} & \frac{\partial N}{\partial x} & 0 \\ 0 & \frac{\partial N}{\partial z} & \frac{\partial N}{\partial y} \\ \frac{\partial N}{\partial z} & 0 & \frac{\partial N}{\partial x} \end{bmatrix} \qquad \mathbf{C'} = \mu \begin{bmatrix}4/3 & -2/3 & -2/3 & 0 & 0 & 0 \\ -2/3 & 4/3 & -2/3 & 0 & 0 & 0 \\ -2/3 & -2/3 & 4/3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (27) |
|} | |} | ||
It must be noted that even for 2D simulations, the terms in <math display="inline">\mathbf{B}</math> and <math display="inline">\mathbf{C'}</math> do not change. The only modification is the elimination of the strains in the third dimension. | It must be noted that even for 2D simulations, the terms in <math display="inline">\mathbf{B}</math> and <math display="inline">\mathbf{C'}</math> do not change. The only modification is the elimination of the strains in the third dimension. | ||
| − | The system of equations [[#eq- | + | The system of equations [[#eq-25|(25)]] can be solved without the use of stabilized formulations, as long as the solid material is not incompressible. Otherwise, the pressure mass matrix becomes zero and therefore stabilization is required. In this case the same stabilization technique used for the fluid elements can be used. |
An additional hypothesis has to be made in order to linearise the system. The transformation of the stresses in the previous configuration to the new configuration requires the updated velocity <math display="inline">\mathbf{V}^{n+1}</math>, making the system non-linear. The simplification used here consists on using the previous step velocity, therefore assuming small accelerations for the solids. This hypothesis is similar to the one used for the convective term, which showed good accuracy in all the cases tested. | An additional hypothesis has to be made in order to linearise the system. The transformation of the stresses in the previous configuration to the new configuration requires the updated velocity <math display="inline">\mathbf{V}^{n+1}</math>, making the system non-linear. The simplification used here consists on using the previous step velocity, therefore assuming small accelerations for the solids. This hypothesis is similar to the one used for the convective term, which showed good accuracy in all the cases tested. | ||
| Line 545: | Line 545: | ||
The fulfilment of the transmission conditions requires that the tractions along the interface must be continuous. Neglecting the air pressure, this condition is satisfied by <math display="inline">\sigma _{xx} = 0</math> at the left and right boundaries of the solid. However, the implemented solid model makes use of the mean pressure in the solid, which means that (taking <math display="inline">\sigma _{zz}=0</math>) the pressure in the solid becomes | The fulfilment of the transmission conditions requires that the tractions along the interface must be continuous. Neglecting the air pressure, this condition is satisfied by <math display="inline">\sigma _{xx} = 0</math> at the left and right boundaries of the solid. However, the implemented solid model makes use of the mean pressure in the solid, which means that (taking <math display="inline">\sigma _{zz}=0</math>) the pressure in the solid becomes | ||
| − | <span id="eq- | + | <span id="eq-28"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 553: | Line 553: | ||
| style="text-align: center;" | <math>\qquad \qquad \qquad p_{solid} = \frac{1}{3} \sigma _{yy} \ne p_{air} </math> | | style="text-align: center;" | <math>\qquad \qquad \qquad p_{solid} = \frac{1}{3} \sigma _{yy} \ne p_{air} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (28) |
|} | |} | ||
| − | The pressure given by [[#eq-44|( | + | The pressure given by [[#eq-44|(28)]] is clearly discontinuous at the interface. If a linear (or any continuous) element was located over the sharp boundary, the discrete pressure field would detect a non-existent gradient that would create normal velocities in the fluid, as seen in Figure [[#img-5|5]]. Since this would violate fluid incompressibility, the solver usually converges to a solution where the last solid node has a very low pressure value and, therefore, the structure is more flexible than it should be. |
<div id='img-5'></div> | <div id='img-5'></div> | ||
| Line 590: | Line 590: | ||
The enrichment functions can be added to the monolithic strategy following a standard condensation procedure <span id='citeF-14'></span>[[#cite-14|[14]]]. Using the subscript <math display="inline">N</math> for the standard shape functions and <math display="inline">*</math> for the enrichment functions, the extended system becomes | The enrichment functions can be added to the monolithic strategy following a standard condensation procedure <span id='citeF-14'></span>[[#cite-14|[14]]]. Using the subscript <math display="inline">N</math> for the standard shape functions and <math display="inline">*</math> for the enrichment functions, the extended system becomes | ||
| − | <span id="eq- | + | <span id="eq-29"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 600: | Line 600: | ||
| style="text-align: center;" | <math> = \left[ \begin{array}{c}\frac{1}{\Delta t} {\mathbf{M_N \bar V_N }}^n + \mathbf{M_N g} \\ {\mathbf{M}_N(\frac{1}{\kappa }) {\bar p}^n_N } \\ {\mathbf{M}_*(\frac{1}{\kappa }) {\bar p}^n_* } \end{array} \right] </math> | | style="text-align: center;" | <math> = \left[ \begin{array}{c}\frac{1}{\Delta t} {\mathbf{M_N \bar V_N }}^n + \mathbf{M_N g} \\ {\mathbf{M}_N(\frac{1}{\kappa }) {\bar p}^n_N } \\ {\mathbf{M}_*(\frac{1}{\kappa }) {\bar p}^n_* } \end{array} \right] </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (29) |
|} | |} | ||
Note that the density <math display="inline">\rho </math> is omitted in the velocity mass matrices due to lack of space. Also, since all mass matrices (both velocity and pressure) are multiplied by <math display="inline">\frac{1}{\Delta t}</math>, this is also omitted for the same reason. To simplify the notation, the system is written as: | Note that the density <math display="inline">\rho </math> is omitted in the velocity mass matrices due to lack of space. Also, since all mass matrices (both velocity and pressure) are multiplied by <math display="inline">\frac{1}{\Delta t}</math>, this is also omitted for the same reason. To simplify the notation, the system is written as: | ||
| − | <span id="eq- | + | <span id="eq-30"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 613: | Line 613: | ||
| style="text-align: center;" | <math>\qquad \left[ \begin{array}{c|c}\mathbf{A_{NN}} & \mathbf{A_{N*}} \\ \mathbf{A_{*N}} & \mathbf{A_{**}} \end{array} \right] \left[ \begin{array}{c}\mathbf{X_{N}} \\ \mathbf{X_{*}} \end{array} \right] = \left[ \begin{array}{c}\mathbf{F_{N}} \\ \mathbf{F_{*}} \end{array} \right] </math> | | style="text-align: center;" | <math>\qquad \left[ \begin{array}{c|c}\mathbf{A_{NN}} & \mathbf{A_{N*}} \\ \mathbf{A_{*N}} & \mathbf{A_{**}} \end{array} \right] \left[ \begin{array}{c}\mathbf{X_{N}} \\ \mathbf{X_{*}} \end{array} \right] = \left[ \begin{array}{c}\mathbf{F_{N}} \\ \mathbf{F_{*}} \end{array} \right] </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (30) |
|} | |} | ||
Condensing the enrichment DoFs the initial size of the system is recovered, as: | Condensing the enrichment DoFs the initial size of the system is recovered, as: | ||
| − | <span id="eq- | + | <span id="eq-31"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 626: | Line 626: | ||
| style="text-align: center;" | <math>\qquad \qquad \qquad \mathbf{\tilde{A}} \mathbf{{X}_N}= \mathbf{\tilde{F}} </math> | | style="text-align: center;" | <math>\qquad \qquad \qquad \mathbf{\tilde{A}} \mathbf{{X}_N}= \mathbf{\tilde{F}} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (31) |
|} | |} | ||
where | where | ||
| − | <span id="eq- | + | <span id="eq-32"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 638: | Line 638: | ||
|- | |- | ||
| style="text-align: center;" | <math>\qquad \qquad \qquad \mathbf{\tilde{A}} = \mathbf{{A}_{NN}} - \mathbf{{A}_{N*}} \mathbf{{A}^{-1}_{**}} \mathbf{{A}_{*N}} </math> | | style="text-align: center;" | <math>\qquad \qquad \qquad \mathbf{\tilde{A}} = \mathbf{{A}_{NN}} - \mathbf{{A}_{N*}} \mathbf{{A}^{-1}_{**}} \mathbf{{A}_{*N}} </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (32) |
|- | |- | ||
| style="text-align: center;" | <math> \qquad \qquad \qquad \mathbf{\tilde{F}} = \mathbf{{F}_{N}} - \mathbf{{A}_{N*}} \mathbf{{A}^{-1}_{**}} \mathbf{{F}_{*}} \mathbf{\tilde{F}} </math> | | style="text-align: center;" | <math> \qquad \qquad \qquad \mathbf{\tilde{F}} = \mathbf{{F}_{N}} - \mathbf{{A}_{N*}} \mathbf{{A}^{-1}_{**}} \mathbf{{F}_{*}} \mathbf{\tilde{F}} </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (33) |
|} | |} | ||
|} | |} | ||
| Line 651: | Line 651: | ||
The solution strategy described in the previous section requires an accurate and robust tool to account for the convective term. Since the aim of the PFEM-2 is to achieve large time steps with small errors, it is not enough to simply move the particles with the last velocity multiplied by the time step (<math display="inline">\delta \mathbf{x} = {V}^n \cdot \Delta _t</math>). | The solution strategy described in the previous section requires an accurate and robust tool to account for the convective term. Since the aim of the PFEM-2 is to achieve large time steps with small errors, it is not enough to simply move the particles with the last velocity multiplied by the time step (<math display="inline">\delta \mathbf{x} = {V}^n \cdot \Delta _t</math>). | ||
| − | The main goal is to obtain as much information as possible from the previous time step to calculate the new position of the particles. The streamline integration method used in this work follows the same strategy of <span id='citeF-1'></span>[[#cite-1|[1]]] for single fluids. For a particle <math display="inline">p</math>, its exact position at time <math display="inline">n+1</math> is computed as [[#eq- | + | The main goal is to obtain as much information as possible from the previous time step to calculate the new position of the particles. The streamline integration method used in this work follows the same strategy of <span id='citeF-1'></span>[[#cite-1|[1]]] for single fluids. For a particle <math display="inline">p</math>, its exact position at time <math display="inline">n+1</math> is computed as [[#eq-34|(34)]]: |
| − | <span id="eq- | + | <span id="eq-34"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 661: | Line 661: | ||
| style="text-align: center;" | <math>\mathbf{x}^{n+1}_p = \mathbf{x}^{n}_p + \int _{n}^{n+1} \mathbf{V^t} dt </math> | | style="text-align: center;" | <math>\mathbf{x}^{n+1}_p = \mathbf{x}^{n}_p + \int _{n}^{n+1} \mathbf{V^t} dt </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (34) |
|} | |} | ||
Unfortunately, the velocity is not known continuously in time but only at discrete time steps( <math display="inline">n-1</math>,<math display="inline">n</math>, <math display="inline">n+1</math> ... ). Approximating the particle trajectory using the velocity of the previous time step to obtain an explicit scheme, the new position of the particle becomes: | Unfortunately, the velocity is not known continuously in time but only at discrete time steps( <math display="inline">n-1</math>,<math display="inline">n</math>, <math display="inline">n+1</math> ... ). Approximating the particle trajectory using the velocity of the previous time step to obtain an explicit scheme, the new position of the particle becomes: | ||
| − | <span id="eq- | + | <span id="eq-35"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 674: | Line 674: | ||
| style="text-align: center;" | <math>\mathbf{x}^{n+1}_p \approx \mathbf{x}^{n}_p + \int _{n}^{n+1} \mathbf{V^n} dt </math> | | style="text-align: center;" | <math>\mathbf{x}^{n+1}_p \approx \mathbf{x}^{n}_p + \int _{n}^{n+1} \mathbf{V^n} dt </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (35) |
|} | |} | ||
| Line 689: | Line 689: | ||
To overcome this problem, the streamline integration must be deactivated when a particle of the heavier fluid transits across a region of the lighter fluid. In this case, the gravity will be taken as the only acting force, leading to a parabolic (projectile-type) motion, where the last known velocity of the particle is taken as the starting data. Setting the distance function <math display="inline">\varphi \le 0</math> for the denser fluid regions and <math display="inline">\varphi > 0 </math> for the lighter fluid regions, the updated position of the denser fluid particles becomes | To overcome this problem, the streamline integration must be deactivated when a particle of the heavier fluid transits across a region of the lighter fluid. In this case, the gravity will be taken as the only acting force, leading to a parabolic (projectile-type) motion, where the last known velocity of the particle is taken as the starting data. Setting the distance function <math display="inline">\varphi \le 0</math> for the denser fluid regions and <math display="inline">\varphi > 0 </math> for the lighter fluid regions, the updated position of the denser fluid particles becomes | ||
| − | <span id="eq- | + | <span id="eq-36"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 697: | Line 697: | ||
| style="text-align: center;" | <math>\mathbf{x}^{n+1}_p \approx \Bigg\{{ \begin{matrix} \mathbf{x}^{n}_p + \int _{n}^{n+1} \mathbf{V^n} dt \qquad \qquad \hbox{if} \varphi _{x_p^t} \le 0 \\ \mathbf{x}^{n}_p + \int _{n}^{n+1} \mathbf{V^n_p} + g\cdot t dt \quad \hbox{if} \varphi _{x_p^t} > 0 \end{matrix} } </math> | | style="text-align: center;" | <math>\mathbf{x}^{n+1}_p \approx \Bigg\{{ \begin{matrix} \mathbf{x}^{n}_p + \int _{n}^{n+1} \mathbf{V^n} dt \qquad \qquad \hbox{if} \varphi _{x_p^t} \le 0 \\ \mathbf{x}^{n}_p + \int _{n}^{n+1} \mathbf{V^n_p} + g\cdot t dt \quad \hbox{if} \varphi _{x_p^t} > 0 \end{matrix} } </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (36) |
|} | |} | ||
| Line 708: | Line 708: | ||
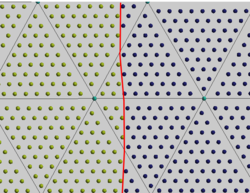
Each particle has an associated material and the interface should be located where the material properties change. The distribution of particles inside each element can define complicated curves that become impossible to manage with simple shape functions due to the large number of particles. As an example, in Figure [[#img-8|8]] some particles are in the "wrong" side of the interface. For this reason the instantaneous local interface inside each element is simply defined by a line (or a plane in 3D) taking into account a weighted average using the shape functions. An instantaneous , pseudo level-set function <math display="inline">\varphi </math> is created that defines the interface where it is valued zero. To calculate the value of <math display="inline">\varphi </math> at each <math display="inline">j</math>th node, all the <math display="inline">i</math> particles in the neighbour elements to <math display="inline">j</math> are used. The weighting function is defined as the standard shape function of the element for the <math display="inline">j</math>th node in the position of each <math display="inline">i</math>th particle. Once the contribution of all the particles has been added, the location of the interface is computed as | Each particle has an associated material and the interface should be located where the material properties change. The distribution of particles inside each element can define complicated curves that become impossible to manage with simple shape functions due to the large number of particles. As an example, in Figure [[#img-8|8]] some particles are in the "wrong" side of the interface. For this reason the instantaneous local interface inside each element is simply defined by a line (or a plane in 3D) taking into account a weighted average using the shape functions. An instantaneous , pseudo level-set function <math display="inline">\varphi </math> is created that defines the interface where it is valued zero. To calculate the value of <math display="inline">\varphi </math> at each <math display="inline">j</math>th node, all the <math display="inline">i</math> particles in the neighbour elements to <math display="inline">j</math> are used. The weighting function is defined as the standard shape function of the element for the <math display="inline">j</math>th node in the position of each <math display="inline">i</math>th particle. Once the contribution of all the particles has been added, the location of the interface is computed as | ||
| − | <span id="eq- | + | <span id="eq-37"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 716: | Line 716: | ||
| style="text-align: center;" | <math>\varphi _ j = \frac{ \sum _{i}^{n} {sign}_i N_i^j}{ \sum _{i}^{n} N_i^j} </math> | | style="text-align: center;" | <math>\varphi _ j = \frac{ \sum _{i}^{n} {sign}_i N_i^j}{ \sum _{i}^{n} N_i^j} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (37) |
|} | |} | ||
| Line 731: | Line 731: | ||
The same procedure is for all the variables, replacing the <math display="inline">sign_i</math> by the desired variable of the particle, either scalar, vectorial or tensorial. Using this kernel, the projected velocity can be written as | The same procedure is for all the variables, replacing the <math display="inline">sign_i</math> by the desired variable of the particle, either scalar, vectorial or tensorial. Using this kernel, the projected velocity can be written as | ||
| − | <span id="eq- | + | <span id="eq-38"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 739: | Line 739: | ||
| style="text-align: center;" | <math>\hat { \hat { \mathbf{V} } } _ j ^{n+1} = \frac{ \sum _{i}^{n} \mathbf{V}_i N_i^j}{ \sum _{i}^{n} N_i^j} </math> | | style="text-align: center;" | <math>\hat { \hat { \mathbf{V} } } _ j ^{n+1} = \frac{ \sum _{i}^{n} \mathbf{V}_i N_i^j}{ \sum _{i}^{n} N_i^j} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (38) |
|} | |} | ||
| Line 746: | Line 746: | ||
It is worth noting that the element shape functions <math display="inline">N_i</math> are not the only possible kernel. As an example, the function proposed in <span id='citeF-16'></span>[[#cite-16|[16]]] for the Smoothed Particle Hydrodynamics method assigns a higher weight to those particles that are closer to the node. Setting <math display="inline">h</math> as the element size and <math display="inline">u=R/h</math>, where <math display="inline">R</math> is the distance from the particle to the node, the Wendland kernel is written as | It is worth noting that the element shape functions <math display="inline">N_i</math> are not the only possible kernel. As an example, the function proposed in <span id='citeF-16'></span>[[#cite-16|[16]]] for the Smoothed Particle Hydrodynamics method assigns a higher weight to those particles that are closer to the node. Setting <math display="inline">h</math> as the element size and <math display="inline">u=R/h</math>, where <math display="inline">R</math> is the distance from the particle to the node, the Wendland kernel is written as | ||
| − | <span id="eq- | + | <span id="eq-39"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 754: | Line 754: | ||
| style="text-align: center;" | <math>W_i^j = \frac{7}{4 \pi h^2}(1+2u)(1-u/2)^4; </math> | | style="text-align: center;" | <math>W_i^j = \frac{7}{4 \pi h^2}(1+2u)(1-u/2)^4; </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (39) |
|} | |} | ||
After the information of the Lagrangian domain has been projected and the mesh computations have been performed, the velocity of the particles has to be updated. At this stage it is important not to replace the particle velocity with the updated velocity but only a correction. The reason for this is simple; no matter how good the kernel algorithm may be, it is never exact. Replacing the unknowns in the particles would destroy valuable data, leading to excessive artificial diffusion in the strategy. Based on this fact, the update stage on the particle will only transfer the variation in the velocity (or any other variable) calculated in the mesh, that is: | After the information of the Lagrangian domain has been projected and the mesh computations have been performed, the velocity of the particles has to be updated. At this stage it is important not to replace the particle velocity with the updated velocity but only a correction. The reason for this is simple; no matter how good the kernel algorithm may be, it is never exact. Replacing the unknowns in the particles would destroy valuable data, leading to excessive artificial diffusion in the strategy. Based on this fact, the update stage on the particle will only transfer the variation in the velocity (or any other variable) calculated in the mesh, that is: | ||
| − | <span id="eq- | + | <span id="eq-40"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 767: | Line 767: | ||
| style="text-align: center;" | <math>\delta \mathbf{V} _ j ^{n+1} = \mathbf{V} _ j ^{n+1} - \hat { \hat { \mathbf{V} } } _ j ^{n+1} </math> | | style="text-align: center;" | <math>\delta \mathbf{V} _ j ^{n+1} = \mathbf{V} _ j ^{n+1} - \hat { \hat { \mathbf{V} } } _ j ^{n+1} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (40) |
|} | |} | ||
| Line 834: | Line 834: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Samper_820077714-rayleigh_geometry2.png| | + | |[[Image:Draft_Samper_820077714-rayleigh_geometry2.png|100px|Rayleigh-Taylor instability geometry]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figure 9:''' Rayleigh-Taylor instability geometry | | colspan="1" | '''Figure 9:''' Rayleigh-Taylor instability geometry | ||
| Line 887: | Line 887: | ||
The beam dimensions are <math display="inline">L=10</math> and <math display="inline">H=1</math>. A vertical mass force of <math display="inline">q = 1[m/s^2]</math> is applied to the whole domain. According to Timoshenko beam theory and correcting the force to account for the buoyancy effect, the vertical displacement <math display="inline">w</math> at the tip should be | The beam dimensions are <math display="inline">L=10</math> and <math display="inline">H=1</math>. A vertical mass force of <math display="inline">q = 1[m/s^2]</math> is applied to the whole domain. According to Timoshenko beam theory and correcting the force to account for the buoyancy effect, the vertical displacement <math display="inline">w</math> at the tip should be | ||
| − | <span id="eq- | + | <span id="eq-41"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 895: | Line 895: | ||
| style="text-align: center;" | <math>w_{max} = (\rho _q - \rho _p) \left(\frac{q L^4}{8 E I} + \frac{1}{2} \frac{q L^2}{10/12 h \mu } \right) = 0.001511 </math> | | style="text-align: center;" | <math>w_{max} = (\rho _q - \rho _p) \left(\frac{q L^4}{8 E I} + \frac{1}{2} \frac{q L^2}{10/12 h \mu } \right) = 0.001511 </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (41) |
|} | |} | ||
| Line 924: | Line 924: | ||
===6.3 Turek FSI benchmark=== | ===6.3 Turek FSI benchmark=== | ||
| − | To test the PFEM-2 algorithm in a fully coupled scenario, the Turek FSI benchmark <span id='citeF-20'></span>[[#cite-20|[20]]], was simulated. This problem is typically used as a reference to validate new FSI strategies and it is particularly challenging for staggered schemes due to the similar properties of the fluid and the solid. On the other hand, the monolithic solver used in this work is well suited for this benchmark. Unlike the previous examples presented in this work (in which the PSPG stabilization was used) in this example the OSS stabilization is employed, with the explicit projection of the pressure gradient in the RHS. This is done to avoid having zeros in the RHS of the pressure equation of Equation [[#eq- | + | To test the PFEM-2 algorithm in a fully coupled scenario, the Turek FSI benchmark <span id='citeF-20'></span>[[#cite-20|[20]]], was simulated. This problem is typically used as a reference to validate new FSI strategies and it is particularly challenging for staggered schemes due to the similar properties of the fluid and the solid. On the other hand, the monolithic solver used in this work is well suited for this benchmark. Unlike the previous examples presented in this work (in which the PSPG stabilization was used) in this example the OSS stabilization is employed, with the explicit projection of the pressure gradient in the RHS. This is done to avoid having zeros in the RHS of the pressure equation of Equation [[#eq-20|(20)]] due to lack of gravity, which would provide excessive numerical diffusion. |
The problem models a 2D rigid cylinder attached to an elastic beam immersed in a fluid stream. The dimensions and problem parameters can be found in <span id='citeF-20'></span>[[#cite-20|[20]]]. In this paper a fixed mesh of 48500 3-noded triangles was used. The frequency and amplitude of the oscillations are analyzed to test the accuracy. For the case studied we use <math display="inline">Re=200</math>, with a parabolic inlet velocity profile and the following parameters: | The problem models a 2D rigid cylinder attached to an elastic beam immersed in a fluid stream. The dimensions and problem parameters can be found in <span id='citeF-20'></span>[[#cite-20|[20]]]. In this paper a fixed mesh of 48500 3-noded triangles was used. The frequency and amplitude of the oscillations are analyzed to test the accuracy. For the case studied we use <math display="inline">Re=200</math>, with a parabolic inlet velocity profile and the following parameters: | ||
| Line 957: | Line 957: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Samper_820077714-turek_snapshot.png| | + | |[[Image:Draft_Samper_820077714-turek_snapshot.png|580px|Turek FSI velocity contour]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figure 15:''' Turek FSI velocity contour | | colspan="1" | '''Figure 15:''' Turek FSI velocity contour | ||
| Line 965: | Line 965: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Samper_820077714-graph_turek.png| | + | |[[Image:Draft_Samper_820077714-graph_turek.png|440px|Tip displacement of the Turek FSI]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figure 16:''' Tip displacement of the Turek FSI | | colspan="1" | '''Figure 16:''' Tip displacement of the Turek FSI | ||
| Line 977: | Line 977: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Samper_820077714-3d_beam_geometry2.png| | + | |[[Image:Draft_Samper_820077714-3d_beam_geometry2.png|410px|Tridimensional Cantilever geometry]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figure 17:''' Tridimensional Cantilever geometry | | colspan="1" | '''Figure 17:''' Tridimensional Cantilever geometry | ||
| Line 984: | Line 984: | ||
For cases in which the density of the fluid is negligible, it is possible to calculate the analytical vibration frequency in vacuum with the following expression: | For cases in which the density of the fluid is negligible, it is possible to calculate the analytical vibration frequency in vacuum with the following expression: | ||
| − | <span id="eq- | + | <span id="eq-42"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 992: | Line 992: | ||
| style="text-align: center;" | <math>\omega _{vac} = \sqrt{\frac{C_n^4 E I}{L^4 \rho _q}} </math> | | style="text-align: center;" | <math>\omega _{vac} = \sqrt{\frac{C_n^4 E I}{L^4 \rho _q}} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (42) |
|} | |} | ||
where the subscript <math display="inline">n</math> denotes the mode and <math display="inline">C_n</math> are the positive roots of the following equation | where the subscript <math display="inline">n</math> denotes the mode and <math display="inline">C_n</math> are the positive roots of the following equation | ||
| − | <span id="eq- | + | <span id="eq-43"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 1,005: | Line 1,005: | ||
| style="text-align: center;" | <math>1 + cos (C_n) cosh (C_n) = 0. </math> | | style="text-align: center;" | <math>1 + cos (C_n) cosh (C_n) = 0. </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (43) |
|} | |} | ||
Taking the first vibration mode, <math display="inline">C_1 = 1.8751</math> and the frequency of the beam becomes: | Taking the first vibration mode, <math display="inline">C_1 = 1.8751</math> and the frequency of the beam becomes: | ||
| − | <span id="eq- | + | <span id="eq-44"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 1,018: | Line 1,018: | ||
| style="text-align: center;" | <math>\omega _{vac} = \sqrt{\frac{C_1^4 E I}{L^4 \rho _q}} = 32.097 rad/s \rightarrow 5.108 Hz </math> | | style="text-align: center;" | <math>\omega _{vac} = \sqrt{\frac{C_1^4 E I}{L^4 \rho _q}} = 32.097 rad/s \rightarrow 5.108 Hz </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (44) |
|} | |} | ||
| Line 1,025: | Line 1,025: | ||
To test the influence of the fluid density, according to Van Eysden <span id='citeF-21'></span>[[#cite-21|[21]]] it is possible to estimate the lower vibration modes for rectangular section beams immersed in a fluid using the following formula: | To test the influence of the fluid density, according to Van Eysden <span id='citeF-21'></span>[[#cite-21|[21]]] it is possible to estimate the lower vibration modes for rectangular section beams immersed in a fluid using the following formula: | ||
| − | <span id="eq- | + | <span id="eq-45"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 1,033: | Line 1,033: | ||
| style="text-align: center;" | <math>\omega _{fluid}=\omega _{vac} \left(1 + \frac{ \pi \rho _p b }{4 \rho _q H } \Gamma _f \right)^{-1/2} </math> | | style="text-align: center;" | <math>\omega _{fluid}=\omega _{vac} \left(1 + \frac{ \pi \rho _p b }{4 \rho _q H } \Gamma _f \right)^{-1/2} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (45) |
|} | |} | ||
| Line 1,070: | Line 1,070: | ||
==8 Acknowledgements== | ==8 Acknowledgements== | ||
| − | This research has been partly funded by the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme FP7/2007-2013/ under REA grant agreement n° 289911. This work was | + | This research has been partly funded by the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme FP7/2007-2013/ under REA grant agreement n° 289911. This work was also supported by the ERC Advanced Grant ‘REALTIME’ project (AdG-2009325), the ERC Advanced Grant ‘SAFECON’ project (AdG-26752), the HFLUIDS project of the National RTD Plan of the Spanish Ministry of Science and Innovation (BIA2010-15880) and the ERC Proof of Concept FORECAST (Ref. 664910) under H2020 Programme. |
The authors would also like to thank Dr. Riccardo Rossi for suggesting the special shape functions used in this work. | The authors would also like to thank Dr. Riccardo Rossi for suggesting the special shape functions used in this work. | ||
Latest revision as of 13:46, 26 March 2019
Published in Computational Mechanics (2015). Vol. 55, pp. 1091–1104
doi: 10.1007/s00466-014-1107-0
Abstract
This paper describes a strategy to solve multi-fluid and Fluid-Structure Interaction (FSI) problems using Lagrangian particles combined with a fixed Finite Element (FE) mesh . Our approach is an extension of the fluid-only PFEM-2 [1][2] which uses explicit integration over the streamlines to improve accuracy. As a result, the convective term does not appear in the set of equations solved on the fixed mesh. Enrichments in the pressure field are used to improve the description of the interface between phases.
Keywords: Multi-fluids FSI Fixed mesh Lagrangian particles Unified approach
1 Introduction
Simulation of Fluid-Structure Interaction (FSI) problems is an area of growing interest due to the several application fields in which it is required. Nowadays all structures, from buildings to airplanes and boats are optimized to minimize weight, leading to a more flexible behaviour in air or water. Furthermore, new areas are always being explored, biomedical research being a fast-growing and stimulating field.
A common approach to treat FSI problems is the staggered or weakly coupled algorithm. This method consists on computing separately the fluid and the solid domain, without ensuring force balance at each time step. The popularity of this method lies in its speed and possibility to use specialized solvers for the structure and the fluid, a desired property since both subdomains are generally treated in different frameworks. While for the structural solver most algorithms employ a Lagrangian reference framework, for the fluid either Eulerian or Arbitrary Lagrangian-Eulerian (ALE) frameworks are used.
On the other hand, in strongly coupled algorithms the solution is considered to converge only when force balance is achieved at the interfaces. To couple the fluid and structural subdomains, monolithic and partitioned strategies have been developed. While the first method consists on assembling and solving all the equations in a single system, the partitioned algorithm solves separately the fluid and solid subdomains, relying on an iterative process to achieve convergence.
A starting point to reduce the complexity of the problem is selecting the right reference framework. An appropriate choice leads to the simplification of complex terms and higher accuracy in the results due to better approximations. Following this line, the Lagrangian framework offers important advantages due to the simplicity of the equations. However, since material points move and the configuration changes continuously in time, it is necessary to couple this set of equations with a strategy that solves for the movement of material points. In [3] a strongly coupled monolithic strategy was proposed for the PFEM to treat simultaneously the fluid and solid phases within the same framework. Using a Lagrangian approach, it was possible to write the momentum equations for both solids and fluids together and seamlessly, with only minor differences due to the stress memory of solids. This allowed us to solve all the equations within a unified computational frame, significantly improving accuracy. On the other hand, to deal with the large deformations experimented by the fluid phase, a remeshing algorithm was implemented. This way distorted meshes were avoided, but with the extra computational cost associated to the Delaunay triangulation meshing stage.
In this work we propose a new method which uses the same discretization and solving technique for all the phases present in the domain. This strategy is an extension of the Particle Finite Element Method-second generation (PFEM-2) developed for multi-fluids in [2]. The PFEM-2 is based on the use of Lagrangian particles with no connectivities to convect all the material properties combined with a fixed mesh, leading to a Lagrangian formulation that does not rely on deforming the spatial mesh nor remeshing.
Since all the material points of the domain are represented by Lagrangian particles, it is possible to convect a large number of variables at very little cost. Furthermore, the convection stage is greatly improved by following the streamlines of the velocity in an explicit way, therefore improving accuracy over first order explicit methods but keeping the computational cost low. Once the particles have been convected, the variables are projected into the mesh, boundaries are identified where material properties change and the Lagrangian system is solved in the fixed mesh. Furthermore, by improving the definition of the interface using enrichment shape functions, the physics of the problem is very closely simulated despite that the mesh does not match the interfaces.
This paper is structured as follows. First, the monolithic strategy of the PFEM-2 is described. In the subsequent sections the strategy for the treatment of the FSI problem is described and finally validation examples are presented.
2 Monolithic strategy for multi-fluids and FSI
2.1 Mixed Framework: The PFEM-2
The current model is based on a mixed Eulerian-Lagran-gian framework, combining advantages of both methods. This is achieved by using a set of particles combined with a fixed FEM mesh in a solving strategy known as PFEM-2 [1]. The method is obtained by writing, for a given particle , the following definition for the position and velocity in a given timestep , where is the velocity and is the acceleration
|
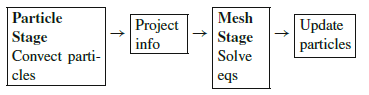
By using an explicit strategy in 1.a, the convective term is completely uncoupled from the momentum equations and Lagrangian equations are obtained. The main advantage of using Lagrangian particles is that the convection is obtained by simply moving the particles across the space and, therefore, the system to be solved does not include the convective term. This set of equations is calculated on the mesh, although it is possible to include partial contributions from the particles to improve accuracy [1]. Then the complete scheme required to solve a step becomes:
The particles used in this scheme do not represent a fixed amount of mass, but rather material points with certain properties and velocity. This allows for a variable number of particles per element depending on the zone, to ensure a better accuracy on selected areas. It must be noted that in the algorithm presented in this paper, the particles are only used to transport information (solve the convective term). However, in certain cases where the viscosity is low and there is a single fluid, it is possible to solve partially the momentum equations (1.b) in the particles, as explained in [1]. Even if this strategy leads to higher accuracy in the cases analysed in that article, it lacks the generality that is required for the simulation of FSI problems.
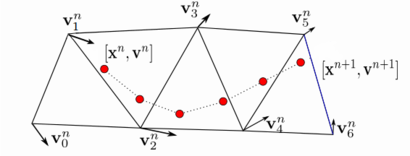
Figure 1 shows the streamline integration for a single particle. This step is purely explicit , which is achieved by convecting the particles using the velocity from the previous time step in a Picard [4] iteration fashion. As for the force integration (if added), information is also gathered from the last step, so the Lagrangian particle solution step remains purely explicit, allowing for a fast computation on each particle that is trivially parallelizable and, hence, fast.
|
| Figure 1: PFEM-2 streamline integration |
Remark: It is possible to imagine this explicit convection as the first step of a non linear iteration process. If an iterative process would be used until convergence, once the new velocity has been calculated, each particle should have its coordinates resetted to the initial position and the streamline integration should be performed again to repeat all the tasks. However, practical experience suggests that the first iteration provides results that are accurate enough, since the numerical data is very close to the experimental results even for very large time steps.
|
| Figure 2: Interface detection using the particles. at the red line. |
Having detected the interface, the system of equation is assembled and solved implicitly. Since the sound speed is infinite in incompressible fluids, the complete set of equations cannot be calculated explicitly.
Finally, once the full system of equations has been solved, corrections are passed to the particles and the cycle is restarted. Details of the convection stage and the procedure for solving the system of equations is explained in the following sections.
2.2 Continuum equations
As explained in the last section, the use of particles allows us to omit the convective term in the momentum equations. The system of equations to be solved in the physical domain is obtained by coupling the momentum balance for a general material with a compressibility/incompressibility equation. Together, these two equations provide exact solutions for problems in which thermal terms are considered to be uncoupled from the mechanical equations
|
Equation (2.a) are complemented by the standard boundary conditions of prescribed velocities and prescribed tractions at the Dirichlet () boundary conditions and Neumann () boundary conditions, respectively.
Equations (2) hold for any material, both fluids and solids, where is the density, the compressibility modulus, the velocity vector, the stress tensor and the mass force vector. In this work fluids are treated as incompressible, meaning that and, therefore, the second equation simplifies for fluids to .
2.2.1 Continuum equations for fluids
For the particular case of fluids, the stress tensor depends only on the current strain rate and the pressure as . Since the aim of this work is to deal with problems of relatively low velocities (where is speed of sound), the fluid will be considered to be incompressible. Replacing into (2), the equations for fluids yields
|
It must be noted that the numerical formulation of this set of equations must be stabilized due to the infinite sound speed caused by the incompressibility constraint.
2.2.2 Continuum equations for solids
The hypoelastic model provides an excellent constitutive model for solids due to its simplicity and direct application for velocity formulations. Hypoelastic materials are those whose stress rate can be defined simply using the rate of deformation tensor as:
|
|
(4) |
where the upper dot represents the time derivative.
The constitutive relationship for hypoelastic materials defines the rate of stress rather than the stress itself. This is particularly useful in the velocity formulation since the rate stress function depends on the rate of deformation (depending on the velocity) instead of the actual deformation. However, the Cauchy stress tensor is not objective (it is affected by rigid body rotations). Therefore, another stress measure is required. Using the Truesdell stress rate and eliminating the stress dependency of the model for simplicity, the stress rate relationship becomes:
|
|
(5) |
The Truesdell rate is related to the Second Piola-Kirchhof (PK2) Stress tensor and provides the exact stress rate for a given deformation as
|
|
(6) |
Using the tensor of elastic moduli for the Truesdell stress rate yields
|
|
(7) |
where and are the Lame parameters. As it can be seen in equation (7) the constitutive expression is not linear since depends on . To overcome this inconvenience, the Jaumann stress rate [5] is used, which simplifies the stress rate into a deformation plus a rotation, avoiding all the non-linear terms. After some algebra, this yields
|
|
(8) |
Approximating the Truessdel stress rate by the Jaumann stress rate gives, combining equations (8) and (6):
|
|
(9) |
We use finite differences in time to obtain
|
|
(10.a) |
Hence,
|
|
(10.b) |
Recalling the relation between the PK2 stress and the Cauchy stress () Equation (10.b) can be expressed as
|
|
(11) |
Resetting the reference framework at each time step as the last known configuration, i.e. , the Cauchy stress for the previous time step directly becomes the PK2 stress , i.e. . Finally the Cauchy stresses in the new configuration are obtained by
|
|
(12) |
or
|
|
(13) |
where the subindex implies that the stresses at time have been updated to the new configuration.
To mimic the formulation of velocities and pressure used in fluids, it is useful to decompose the stresses into the pressure caused by the volumetric deformation and the deviatoric part caused by the deviatoric strain . Introducing this splitting in (13) yields
|
|
(14) |
Finally,
|
|
(15) |
where
|
Equations (15) and (16) provide the expressions for updating the stresses at each time step. A more detailed explanation can be found in [3] and [6].
3 Fixed mesh domain
3.1 Spatial discretization
The chosen spatial discretization procedure is the Finite Element Method (FEM) [7]. It consists on dividing the domain into elements, whose geometry is defined by nodes. The unknown variables are the values at the nodes and the solution is interpolated from the nodal values inside each element. In this work linear shape functions will be used for all the variables. Three-noded triangles (2D) and 4-noded tetrahedra will be used for all the examples shown in this work. Using the FEM discretization and the test functions for the velocity and for the pressure, the weak form [7] of the system 2.2 becomes
|
Note that the stress term is integrated by parts to avoid second space derivatives on the shape functions.
In Eq.(17.a), are the prescribed tractions on the Neumann boundaries . On the other hand, we have omitted the boundary terms that appear due to the integration by parts. These terms are the boundary traction terms at the edges of all the elements in the mesh, with the normal vectors pointing outwards. Omitting these terms ensures that traction stress continuity is fulfilled on the inter-element boundaries, where and are the boundaries of two adjacent elements, i.e.
|
|
(18) |
Ensuring that Eq.(18) is satisfied is of particular interest in this work since the pressure field has to be discontinous between interfaces due to the different material properties. Fullfilling this requirement by omitting this boundary term provides a straightforward yet accurate approach, even if discontinuities occur in the pressure field.
Using a Galerkin method (with , where is the shape functions matrix) the set of algebraic equations from 3.1 can be written as
|
|
(19) |
In Eq. (19), first order finite differences are used in the acceleration term to advance in time and denotes nodal variables. The sub-matrices of the system are the standard ones obtained after using the Galerkin FEM for fluid problems [8].
3.2 Stabilized matrix form for the fluid phase
A FEM discretization directly implemented in the form (19) using the same shape functions for the velocity and the pressure would be unstable in the pressure since it does not satisfy the inf-sup condition [9]. Moreover, even if different functions were to be used to avoid this restriction, the system of equations would not be suited for several linear solvers since it contains zeros in the diagonal terms of the pressure equation as seen in the matrix form (19).
In order to overcome this limitation, stabilization terms can be added to the set of equations (19). As stated before, it is necessary to stabilize the pressure equation for the fluid problem only. While there are several methods to do so, only two will be mentioned in this work: the Pressure-Stabilizing/Petrov-Galerkin (PSPG) method [10] and the Orthogonal Subgrid Scale (OSS) stabilization [11]. The reason behind this is that both methods add a Laplacian to the LHS of the system of equations (19), thus preserving the symmetry of the system.
In Eq. (20) the final matrix system is presented for the PSPG method. Using the OSS method with an explicit projection stage would lead to a similar expression but with the explicit projection of the pressure in the RHS.
|
|
(20) |
In Equations (23), is the Laplacian of the pressure. Another alternative to stabilize the equations is the Finite Increment Calculus (FIC) procedure [6].The FIC method avoids the need to prescribe the pressure in free surface solvers using staggered schemes. A mixed FEM Lagrangian formulation for treating both quasi and fully incompressible fluids as well as FSI problems using the FIC method is presented in [6].
The system (20) can be solved by choosing an appropriate stabilization parameter . In this work following the work in [12][10]. The dependency on was added to avoid when the velocity and the viscosity are zero [10].
3.3 Matrix form for the solid phase
Unlike fluids, solids will not be considered incompressible. The spatial discretization and variables will be the same as for the fluids formulation: linear elements for both the pressure and the velocity. As for the deviatoric stress, it will not be an independent variable, but a state variable depending on the velocity unknowns.
Recalling the general system of Eqs. (2) and splitting the stresses into its deviatoric and volumetric components, the system of governing equations reads:
|
The weak form of the problem is
|
A first approximation in time for the velocity would lead to a stable but too diffusive algorithm. To avoid this shortcoming, the Newmark's Beta method was selected. Parameters were set for constant acceleration. The resulting expression for the velocity integration becomes:
|
|
Using finite differences in time for the pressure, dividing the second equation by the compressibility modulus and recalling the definition of the stresses (15) yields:
|
|
(23) |
The rate of defomations is calculated implicitly to avoid instabilities as
|
|
(24) |
where is the standard strain-rate velocity matrix (27). Finally, writing the equations in matrix form, the system can be expressed as:
|
|
(25) |
In general all the matrices have the same form used for the fluid elements, except for the stiffness matrix . Its expression is:
|
|
(26) |
where is the constitutive matrix for the deviatoric stresses. The expressions for and for 3D problems are
|
|
(27) |
It must be noted that even for 2D simulations, the terms in and do not change. The only modification is the elimination of the strains in the third dimension.
The system of equations (25) can be solved without the use of stabilized formulations, as long as the solid material is not incompressible. Otherwise, the pressure mass matrix becomes zero and therefore stabilization is required. In this case the same stabilization technique used for the fluid elements can be used.
An additional hypothesis has to be made in order to linearise the system. The transformation of the stresses in the previous configuration to the new configuration requires the updated velocity , making the system non-linear. The simplification used here consists on using the previous step velocity, therefore assuming small accelerations for the solids. This hypothesis is similar to the one used for the convective term, which showed good accuracy in all the cases tested.
3.4 Special considerations on the interface
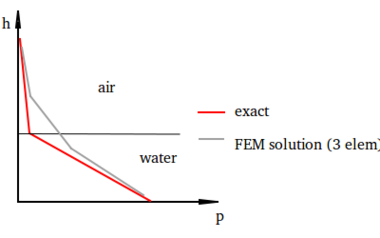
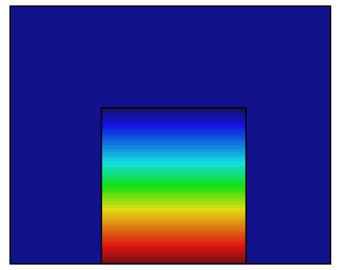
Despite the advantages that the FEM discretization provides, it bears a severe limitation when the variables undergo abrupt changes that the chosen FEM space is unable to reproduce. As an example,when there is a sharp change of the density in a two-fluid problem, the hydrostatic condition under the gravitational force leads to two different values for the pressure gradient. This is specially critical when the fluids have very different densities (i.e. air-water), where the term changes abruptly at the interface.
|
| Figure 3: Pressure distribution for the hydrostatic case |
Figure 3 shows the exact pressure distribution for the hydrostatic case of water and air and the one obtained using three linear elements. It is clear that this solution is very poor and in practice it would lead to an incorrect behavior of the interface and mass losses [13].
When dealing with FSI problems, this issue is even more critical. The reason for this is again the strong discontinuity in the material properties, in this case the stiffness (or the viscosity). A simple example to illustrate this is a box of a solid material surrounded by air under gravitational force. In this case the pressure distribution would take the shape illustrated in Figure 4.
|
| Figure 4: Pressure distribution of a solid body surrounded by air under gravitational force |
The fulfilment of the transmission conditions requires that the tractions along the interface must be continuous. Neglecting the air pressure, this condition is satisfied by at the left and right boundaries of the solid. However, the implemented solid model makes use of the mean pressure in the solid, which means that (taking ) the pressure in the solid becomes
|
|
(28) |
The pressure given by (28) is clearly discontinuous at the interface. If a linear (or any continuous) element was located over the sharp boundary, the discrete pressure field would detect a non-existent gradient that would create normal velocities in the fluid, as seen in Figure 5. Since this would violate fluid incompressibility, the solver usually converges to a solution where the last solid node has a very low pressure value and, therefore, the structure is more flexible than it should be.
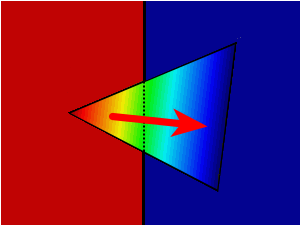
|
| Figure 5: Close-up of a linear element located at the interface showing the interpolated pressure field |
3.5 Raising the limitations: pressure enrichments
To overcome the problems of standard finite elements, the space must be modified to allow for a more accurate reproduction of the solution. A first alternative would be remeshing the zone crossed by the interface. This would lead to the exact solution but would require adding new degrees of freedom (DoFs) to the new discretized geometry. This strategy, despite being possible, is computationally expensive since the system must be resized and new memory space must be allocated in the memory, task that is likely to be slower than the solution of the system itself.
An alternative to a new mesh is enrichening the FEM space. Enriching consist on creating new DoFs on each side of the interface elements and then statically condensing the new unknowns [14].
In [15] it is shown that the solution improves when more flexibility is given to the pressure field at the interface. Following this line, three enrichments shape functions plus special shape functions to replace the standard pressure field are used. Figure 6 shows that a total of 6 functions are used, with the goal of fully uncoupling the pressure from both sides. To do so, first the standard shape functions in the interface elements are replaced by their discontinuous counterparts. These functions are basically the same as the original ones, but the integrals are calculated only with the contribution of the partitions whose sign matches the sign of the node. On the other hand, when partitions and nodes have different signs, the contribution is added to the enrichments functions or . In other words, the original shape functions are split in two independent functions across the interface. This allows more freedom in the pressure field, while retaining the partition of unity [7].
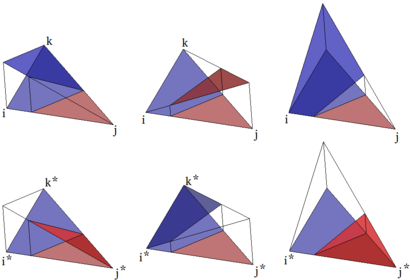
|
| Figure 6: Pressure shape functions: Top: Replacement functions. Bottom: Enrichments |
Stabilizing the pressure equation in the fluid phase is equivalent to adding artificial diffusion to this variable. Therefore, adding stabilization to the interface elements would inevitably lead to an inaccurate behavior of the solid phase due to dissipation of the stresses in the interface region. For this reason no stabilization is used in these elements. However, as stated previously, doing so would cause instabilities due to the non-fulfilment of the inf-sup condition [11]. To override this problem, both sides of the interface are considered to be compressible (using the compressibility modulus of the solid phase). While this hypothesis is not correct, it leads to small errors only since the fluid volume is changed only when there is a sharp change in the pressure from one timestep to the next. This strategy yields almost exact results, avoiding pressure diffusion across the interface with minimal errors.
Remark: One of the advantages of this set of discontinuous functions is that the partition of unity is conserved. But most importantly, this also implies that the reconstruction of the pressure after convection is easier to perform accurately. The strategy currently implemented consists on the following steps. First, a standard nodal projection algorithm is used and, therefore, the values of the replacement shape functions are set. Having done this, the enrichment shape functions are defined as the mean of the real nodal values for the previous timestep . This ensures that the prediction for the gradient in the normal direction is minimized, thus reducing spurious velocities.
3.5.1 Adding the new DoFs to the system of equations
The enrichment functions can be added to the monolithic strategy following a standard condensation procedure [14]. Using the subscript for the standard shape functions and for the enrichment functions, the extended system becomes
|
|
(29) |
Note that the density is omitted in the velocity mass matrices due to lack of space. Also, since all mass matrices (both velocity and pressure) are multiplied by , this is also omitted for the same reason. To simplify the notation, the system is written as:
|
|
(30) |
Condensing the enrichment DoFs the initial size of the system is recovered, as:
|
|
(31) |
where
|
4 Lagrangian particles domain
4.1 Streamline integration
The solution strategy described in the previous section requires an accurate and robust tool to account for the convective term. Since the aim of the PFEM-2 is to achieve large time steps with small errors, it is not enough to simply move the particles with the last velocity multiplied by the time step ().
The main goal is to obtain as much information as possible from the previous time step to calculate the new position of the particles. The streamline integration method used in this work follows the same strategy of [1] for single fluids. For a particle , its exact position at time is computed as (34):
|
|
(34) |
Unfortunately, the velocity is not known continuously in time but only at discrete time steps( ,, ... ). Approximating the particle trajectory using the velocity of the previous time step to obtain an explicit scheme, the new position of the particle becomes:
|
|
(35) |
While this approximation may be valid for quasi-stationary problems, it can lead to severe errors in transient situations. In [1] it was shown that this strategy provides good results for single fluids. However in multi-fluids and FSI problems the difference in the properties, in particular the density, makes this approximation unsuitable for some cases. When the density jump is important, one fluid dominates over the other and their behaviour is completely different (ie: air and water). As an example, a breaking wave is represented in Figure 7. Following the air streamlines to predict the water particle trajectory would lead to large errors.
|
| Figure 7: Breaking wave with two fluids. Blue line: Streamline at ; Green line: Actual particle trajectory |
To overcome this problem, the streamline integration must be deactivated when a particle of the heavier fluid transits across a region of the lighter fluid. In this case, the gravity will be taken as the only acting force, leading to a parabolic (projectile-type) motion, where the last known velocity of the particle is taken as the starting data. Setting the distance function for the denser fluid regions and for the lighter fluid regions, the updated position of the denser fluid particles becomes
|
|
(36) |
It is important to note that this method is purely explicit and, therefore, no further corrections are done for computing the convective term. Even though an iterative process could be performed to improve the accuracy, in all the examples solved with this strategy the errors were small, despite the large time steps chosen. This is specially interesting since the PFEM-2 was compared against other algorithms that make use of implicit strategies and yet they have to rely on smaller time steps to obtain similar results. Based on these tests it was decided to keep only the explicit computation of the convective term, since it provides an excellent balance between computation time and accuracy.
4.2 Projection kernel
Once the particles have been convected to their new position, , it is necessary to project the information into the mesh in order to solve the Lagrangian system of equations. The simplest projection kernel consists on directly using the shape functions of the elements. As an example, the definition of the interface for two materials is explained next.
Each particle has an associated material and the interface should be located where the material properties change. The distribution of particles inside each element can define complicated curves that become impossible to manage with simple shape functions due to the large number of particles. As an example, in Figure 8 some particles are in the "wrong" side of the interface. For this reason the instantaneous local interface inside each element is simply defined by a line (or a plane in 3D) taking into account a weighted average using the shape functions. An instantaneous , pseudo level-set function is created that defines the interface where it is valued zero. To calculate the value of at each th node, all the particles in the neighbour elements to are used. The weighting function is defined as the standard shape function of the element for the th node in the position of each th particle. Once the contribution of all the particles has been added, the location of the interface is computed as
|
|
(37) |
where denotes the sign of the particle, positive () for the lighter fluid and negative () for the denser fluid.
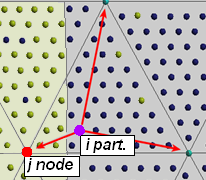
|
| Figure 8: Contribution of particle to the node |
The same procedure is for all the variables, replacing the by the desired variable of the particle, either scalar, vectorial or tensorial. Using this kernel, the projected velocity can be written as
|
|
(38) |
The in the notation implies that it is the first approximation of the velocity, taking into account only the convecting term and neglecting all the other contributions. This velocity will be used as the starting point for the finite element fixed mesh solver
It is worth noting that the element shape functions are not the only possible kernel. As an example, the function proposed in [16] for the Smoothed Particle Hydrodynamics method assigns a higher weight to those particles that are closer to the node. Setting as the element size and , where is the distance from the particle to the node, the Wendland kernel is written as
|
|
(39) |
After the information of the Lagrangian domain has been projected and the mesh computations have been performed, the velocity of the particles has to be updated. At this stage it is important not to replace the particle velocity with the updated velocity but only a correction. The reason for this is simple; no matter how good the kernel algorithm may be, it is never exact. Replacing the unknowns in the particles would destroy valuable data, leading to excessive artificial diffusion in the strategy. Based on this fact, the update stage on the particle will only transfer the variation in the velocity (or any other variable) calculated in the mesh, that is:
|
|
(40) |
4.3 Computational issues and code speed
The code used in this work was developed in the C++ programming environment KRATOS [17]. KRATOS is an open-source multi-physics software framework mainly designed for the FEM, which eases the tasks that are common to all FEM codes, such as the assembly of the system of equations or implementing an efficient solver. Ensuring low execution times at the particles convection stage is critical since the number of particles is 10 to 20 times larger than the number of elements in the mesh for a given domain, meaning that millions of particles have to be displaced at each time step for large problems. The optimization and parallelization of this stage lead to a code that spends approximately half of the execution time on particle tasks and the other half on the solution of the implicit system of equations in the mesh.
The current implementation of this work is capable of solving two phase flows accurately and with execution times similar, or even faster, than industry standard codes such as OpenFoam, as shown in [1] for one phase flows and in [2] for multi-fluids.
5 Full PFEM-2 algorithm
Coupling the strategy described in the previous sections, the PFEM-2 solver for multi-fluids and FSI is obtained. The solution steps within a time step can be summarized as follows:
Step 1) Convect the particles using the streamlines}
Step 2) Project information on the mesh, with fluid particles and solid particles
|
|
Step 3) Detect interface elements
Step 4) Estimate pressure enrichments
Step 5) Assemble the system with enrichments
Step 6) Solve the system of equations
Step 7) Recover condensed DoFs
Step 8) Update the velocity, pressure and stress at the particles
6 Numerical Examples
6.1 Rayleigh-Taylor instability
The classical Rayleigh-Taylor instability benchmark for multi-fluids was tested to verify the PFEM-2 solver. Despite there are no analytical results or experimental data in 2D to check the error, it is possible to compare the solution against other numerical results. He et al. [18] presented results for a Reynolds number using a Lattice Boltzmann scheme. With the same initial conditions, results for can be found in [19]. The geometry of the two-fluid problem can be seen Figure 9. We have used a mesh of 163000 3-noded triangles. The parameters of the simulation are:
Initial conditions:
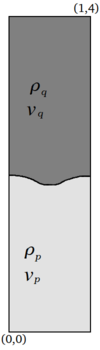
|
| Figure 9: Rayleigh-Taylor instability geometry |
Figure 11 shows snapshots of the two-fluid problem at different time steps. For the Reynolds number analysed, the results obtained match the ones found in [19][18]. The non-dimensional time is used. Finally the position of the advancing front of the denser fluid (centre) and the rising of the bubbles (walls) are compared to the results of [19]. Again good matching is observed.
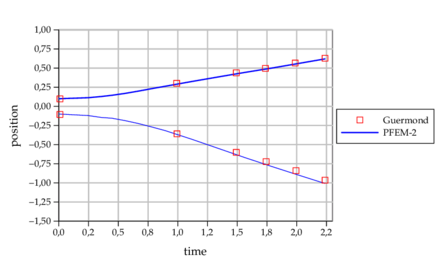 ] ]
|
| Figure 10: Vertical position of the advancing front and bubbles in the Rayleigh-Taylor instability for [19] |
| ||||||
| Figure 11: Snapshots for the Rayleigh-Taylor instability two-fluid problem at . |
6.2 Static cantilever beam immersed in fluid
To test the accuracy of the solver and the potential of the enrichment functions to uncouple the pressure, the following numerical example was designed. A beam under small deformations is surrounded by a very light fluid. Inertial terms are neglected to test the static solution, leading to a Stokes problem in the fluid. The viscosity is set as small as possible to allow for a faster convergence to the statical solution while maintaining stability. The geometry is depicted in Figure 12. The material properties are:
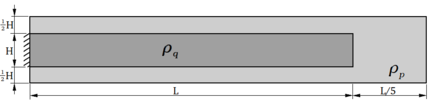
|
| Figure 12: Cantilever beam with fluid geometry |
The beam dimensions are and . A vertical mass force of is applied to the whole domain. According to Timoshenko beam theory and correcting the force to account for the buoyancy effect, the vertical displacement at the tip should be
|
|
(41) |
Structured meshes with decreasing element size were created to check convergence. Mesh sizes from to were used. To test the influence of the projection algorithm, the simulation was run with and without projection. In the latter case, the nodal pressure is kept as a nodal variable from one time-step to the next instead of being obtained from the particles using the projection kernel.
In order to test the behaviour of the splitted elements, the interface between the solid phase and the fluid phase is located in all the meshes at approximately the middle of the elements, as shown in Figure 13. In this case the enrichment shape functions in the pressure are imperative due to the strong discontinuity of the material properties, leading to a jump in the pressure field. If this variable was not enriched to allow for discontinuities, a strong pressure gradient would appear at the interface and, therefore, the resulting velocity field would be inaccurate. It must be noted that Figure 13 does not correctly represent the pressure at the interface elements, since the field is printed using linear interpolation, while in fact it is discontinuous due to the enrichments.

|
| Figure 13: Beam interface and pressure distribution |
Figure 14 clearly shows the detrimental effect of the projection stage. While the algorithm without projection is able to maintain the quadratic convergence of the solid-only case, the results with projection show a convergence slope of only .
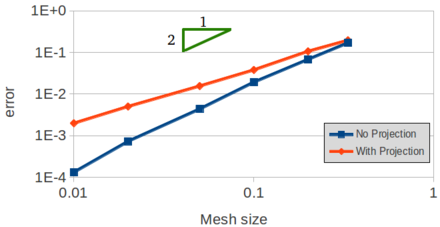
|
| Figure 14: Convergence for the cantilever beam in fluid |
Despite the solver with the projection stage provides a less accurate solution, it leads to acceptable errors for all the mesh sizes chosen. Even for coarse meshes of only three elements along the thickness, the errors are still low (at around 10 % ).
6.3 Turek FSI benchmark
To test the PFEM-2 algorithm in a fully coupled scenario, the Turek FSI benchmark [20], was simulated. This problem is typically used as a reference to validate new FSI strategies and it is particularly challenging for staggered schemes due to the similar properties of the fluid and the solid. On the other hand, the monolithic solver used in this work is well suited for this benchmark. Unlike the previous examples presented in this work (in which the PSPG stabilization was used) in this example the OSS stabilization is employed, with the explicit projection of the pressure gradient in the RHS. This is done to avoid having zeros in the RHS of the pressure equation of Equation (20) due to lack of gravity, which would provide excessive numerical diffusion.
The problem models a 2D rigid cylinder attached to an elastic beam immersed in a fluid stream. The dimensions and problem parameters can be found in [20]. In this paper a fixed mesh of 48500 3-noded triangles was used. The frequency and amplitude of the oscillations are analyzed to test the accuracy. For the case studied we use , with a parabolic inlet velocity profile and the following parameters:
In Figure 15 the velocity contour is plotted after the stationary regime has been achieved. Finally, in Figure 16 the vertical displacement of the tip can be observed. In Table 1 the results are analysed. Compared to Turek's solution, both the amplitude and the frequency are 10 % below the reference value. This result is considered acceptable since only ten 3-noded triangular elements have been used to discretize the beam thickness.
| Frequency | Amplitude | |
| Turek | 5.3 | 0.0707 |
| PFEM2 | 4.8 | 0.0610 |

|
| Figure 15: Turek FSI velocity contour |
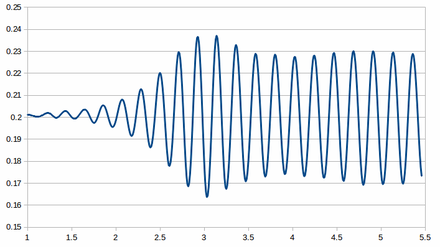
|
| Figure 16: Tip displacement of the Turek FSI |
6.4 3D benchmark. Dynamic cantilever beam
The last example tests the PFEM-2 algorithm in 3D dynamic problems. The same geometry of the previous 2D cantilever beam was selected but restoring the inertial terms and taking the width to obtain a square section. The geometry can be seen in Figure 17, with a vertical mass force to initiate the movement. The mesh size is in the surroundings of the beam and in the distant fluid areas, for a total of 283500 4-noded tetrahedra and more than four million particles. The time step is set for and the properties of the solid are the same as the 2D static cantilever beam example. The subindexes and are used for the solid and fluid properties respectively
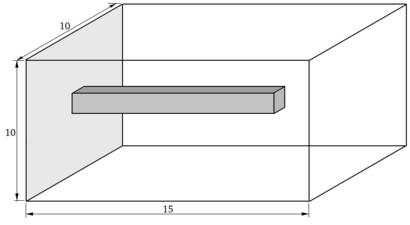
|
| Figure 17: Tridimensional Cantilever geometry |
For cases in which the density of the fluid is negligible, it is possible to calculate the analytical vibration frequency in vacuum with the following expression:
|
|
(42) |
where the subscript denotes the mode and are the positive roots of the following equation
|
|
(43) |
Taking the first vibration mode, and the frequency of the beam becomes:
|
|
(44) |
The frequency observed in the simulation for low fluid densities () is , in good agreement with the theoretical value. The slightly higher value is caused by the low number of elements in the thickness, which leads to a stiffer behavior.
To test the influence of the fluid density, according to Van Eysden [21] it is possible to estimate the lower vibration modes for rectangular section beams immersed in a fluid using the following formula:
|
|
(45) |
where and are the height and width of the beam and is the hydrodynamic function which depends on the viscosity and the cross section of the beam. For inviscid flows and square sections [22].
Fluid densities from to were selected to validate the algorithm. The results can be seen in Figure 18, toghether with the comparison against Equation (71). Analyzing this graph, it is clear that the numerical solution diverges from the expected curve as the fluid density increases. This is caused by the limitations of the standard linear elements used for the velocity field, which lead to interface elements that are assembled with averaged stiffness properties between the fluid and the solid and, therefore, the added mass effect is larger than it should be.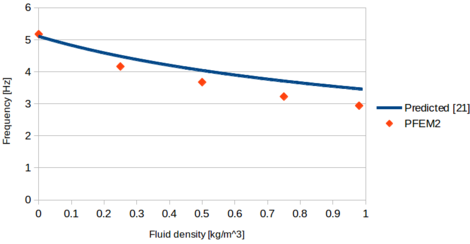
|
| Figure 18: Oscillation frequency of the 3D cantillever beam for different fluid densities |
To analyze the convergence of the method with the mesh size, the case with a fluid density was selected. Mesh sizes from to were chosen (3 to 12 elements in the thickness of the beam). In all cases the interface was located in the middle of the elements to test the worst scenario.
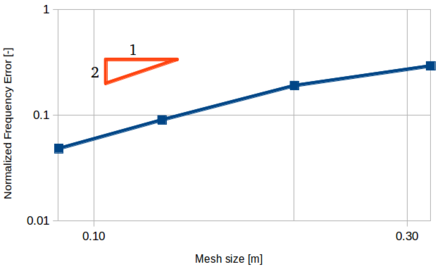
|
| Figure 19: Mesh convergence for the oscillation frequency of the 3D cantilever beam |
A quadratic convergence with the mesh size can be observed in Figure 19, indicating that the interaction between the fluid and the beam is accurately simulated.
7 Conclusions and remarks
A numerical method to solve monolithically multi-fluids and FSI problems was developed. The strategy is based on the PFEM-2 technique originally formulated in [1] for homogeneous fluids, which allows for fast computations while maintaining accuracy.
The enhanced PFEM-2 algorithm makes use of Lagrangian particles and a fixed mesh. Several enrichment degrees of freedom (DoFs) are added in the mesh to improve the pressure field at the interfaces. Adding extra DoFs allows for a more accurate capturing of the solution where the material properties change abruptly, since this leads to discontinuities of the pressure or its gradients. On the other hand, to avoid resizing the system of equations, the new variables are statically condensed and, hence, the computation times are not significantly increased.
The 3D example presented shows that the standard velocity field might not be accurate for coarse meshes due to the artificial added mass effect caused by the FEM linear shape functions. As a possible solution, enrichening the velocity variables to improve the definition of the interface would reduce the errors without the need for refining the mesh.
More advanced constitutive models are also needed to account for a more realistic simulation of complex phenomena such as debris flows, both at the solid stage and the rheological behaviour of the flow. This would allow to simulate all the phenomena in this type of problem, from initiation to deposition of the eroded material using a single and accurate tool.
8 Acknowledgements
This research has been partly funded by the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme FP7/2007-2013/ under REA grant agreement n° 289911. This work was also supported by the ERC Advanced Grant ‘REALTIME’ project (AdG-2009325), the ERC Advanced Grant ‘SAFECON’ project (AdG-26752), the HFLUIDS project of the National RTD Plan of the Spanish Ministry of Science and Innovation (BIA2010-15880) and the ERC Proof of Concept FORECAST (Ref. 664910) under H2020 Programme.
The authors would also like to thank Dr. Riccardo Rossi for suggesting the special shape functions used in this work.
References
[1] Idelsohn, S. and Nigro, N. and Gimenez, J. and Rossi, R. and Marti, J. (2013) "A fast and accurate method to solve the incompressible Navier-Stokes equations", Volume 30. Emerald Group Publishing Limited. Engineering Computations 2 2–2
[2] Idelsohn, Sergio R and Marti, Julio and Becker, Pablo and Oñate, Eugenio. (2014) "Analysis of multifluid flows with large time steps using the particle finite element method". Wiley Online Library. Int. J. Numer. Meth. Fluids
[3] Idelsohn, Sergio R and Marti, Julio and Limache, A and Oñate, Eugenio. (2008) "Unified Lagrangian formulation for elastic solids and incompressible fluids: application to fluid–structure interaction problems via the PFEM", Volume 197. Elsevier. Comput. Method. Appl. M. 19 1762–1776
[4] DeBlois, Bruce M. (1997) "Linearizing convection terms in the Navier-Stokes equations", Volume 143. Elsevier. Comput. Method. Appl. M. 3 289–297
[5] Belytschko, Ted and Liu, Wing Kam and Moran, Brian and Elkhodary, Khalil. (2013) "Nonlinear Finite Elements for Continua and Structures". John Wiley & Sons
[6] Oñate, Eugenio and Franci, Alessandro and Carbonell, Josep M. (2014) "A particle finite element method for analysis of industrial forming processes", Volume 54. Springer. Comput. Mech. 1–23
[7] Zienkiewicz, O.C. and Taylor, R.L. and Zhu, J. Z. (2006) "The Finite Element Method: Its Basic and Fundamentals", Volume 1. Elsevier, 6th Edition
[8] Donea, J. and Huerta, H. (2003) "Finite Element Methods for Flow Problems". John Wiley and Sons
[9] Codina, Ramon and Badia, Santiago. (2006) "On some pressure segregation methods of fractional-step type for the finite element approximation of incompressible flow problems", Volume 195. Elsevier. Comput. Method. Appl. M. 23 2900–2918
[10] Tezduyar, Tayfun E. (1992) "Stabilized finite element formulations for incompressible flow computations", Volume 28. Elsevier. Adv. Appl. Mech. 1–44
[11] Codina, Ramon. (2000) "Stabilization of incompressibility and convection through orthogonal sub-scales in finite element methods", Volume 190. Elsevier. Comput. Method. Appl. M. 13 1579–1599
[12] Oñate, Eugenio and Franci, Alessandro and Carbonell, Josep M. (2014) "Lagrangian formulation for finite element analysis of quasi-incompressible fluids with reduced mass losses", Volume 74. Wiley Online Library. Int. J. Numer. Meth. Fluids 10 699–731
[13] Coppola, H. (2009) "A finite element model for free surface and two fluid flows on fixed meshes". Universitat Politecnica de Catalunya
[14] Felippa, C. A. (2004) "Introduction to finite element methods". University of Colorado, Boulder, http://www. colorado. edu/engineering/CAS/courses. d/IFEM. d
[15] Ausas, Roberto F and Buscaglia, Gustavo C and Idelsohn, Sergio R. (2012) "A new enrichment space for the treatment of discontinuous pressures in multi-fluid flows", Volume 70. Wiley Online Library. Int. J. Numer. Meth. Fluids 7 829–850
[16] Wendland, Holger. (1995) "Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree", Volume 4. Springer. Adv. Comput. Math. 1 389–396
[17] Dadvand, Pooyan and Rossi, Riccardo and Oñate, Eugenio. (2010) "An object-oriented environment for developing finite element codes for multi-disciplinary applications", Volume 17. Springer. Arch. Comput. Method E. 3 253–297
[18] He, Xiaoyi and Chen, Shiyi and Zhang, Raoyang. (1999) "A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh–Taylor instability", Volume 152. Elsevier. J. Comput. Phys. 2 642–663
[19] Guermond, J-L and Quartapelle, L. (2000) "A projection FEM for variable density incompressible flows", Volume 165. Elsevier. J. Comput. Phys. 1 167–188
[20] Turek, Stefan and Hron, Jaroslav. (2006) "Proposal for numerical benchmarking of fluid-structure interaction between an elastic object and laminar incompressible flow". Springer
[21] Van Eysden, Cornelis A and Sader, John E. (2006) "Resonant frequencies of a rectangular cantilever beam immersed in a fluid", Volume 100. AIP Publishing. J. Appl. Phys. 11 114916
[22] Brumley, Douglas R and Willcox, Michelle and Sader, John E. (2010) "Oscillation of cylinders of rectangular cross section immersed in fluid", Volume 22. AIP Publishing. Phys. Fluids (1994-present) 5 052001
Document information
Published on 01/01/2015
DOI: 10.1007/s00466-014-1107-0
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?