donde ${\textstyle \,l}$ es la longitud de la arista del elemento finito dañado, ${\textstyle {\sigma }_{f}}$ es el límite elástico a tracción del material, ${\textstyle G}$ la energía de fractura y ${\textstyle {E}_{0}}$ el módulo de Young del material no dañado. Resulta obvio que entre dos pasos de tiempo el daño de un lado o una arista no puede disminuir, ya que ello implicaría la reparación espontánea del material, lo cual es termodinámicamente inadmisible.

3.2 Definición del daño elemental

Una vez que el daño ha sido evaluado en cada lado o arista de un elemento (es decir, un enlace virtual entre elementos discretos) el daño sobre el conjunto del elemento se calcula como el máximo daño existente en todos los planos que cortan un triángulo (2D) o un tetraedro (3D) (Fig. 1). En cada tetraedro existen cuatro planos de corte que aíslan un vértice (Fig. 1b) y otros tres que aíslan dos vértices (Fig. 1c). De esta manera, el daño sobre el plano de corte se define como el valor medio del daño de cada arista del elemento que corta dicho plano.

Figura 1. Planos de corte. a) Elemento triangular b) Tetraedro aislando un vértice c) Tetraedro aislando dos vértices.

4.- Discretización mediante DEM

En problemas 3D, la fuerza normal de contacto se genera en el punto de contacto entre dos esferas y viene dada por.

La fuerza tangencial ${\textstyle {F}_{s}}$ en el punto de contacto se descompone en dos direcciones ortogonales ${\textstyle {s}_{1}}$ y ${\textstyle {s}_{2}}$ contenidas en el plano normal a la dirección ${\textstyle {d}_{ij}}$. Para cada dirección ${\textstyle {s}_{i}}$ la fuerza tangencial se describe por

Es importante mencionar que la estrategia del uso de elementos discretos para definir el contacto entre los labios de una fisura permite resolver problemas estructurales en donde existe apertura y cierre de múltiples grietas, como se muestra en el análisis sísmico de un edificio histórico de mampostería, presentado al final de este artículo.

6.- Integración temporal en sub-pasos

Uno de los principales problemas en el análisis 3D en el tiempo es el gran número de ecuaciones que surgen de la discretización. Sumando a estos la dificultad para considerar un gran período de tiempo, se concluye que en problemas dinámicos la integración implícita en el tiempo es la mejor estrategia de solución. Sin embargo, este tipo de integraciones son complejas de utilizar en el DEM debido a que es imposible identificar y cuantificar correctamente los contactos y las fuerzas de contacto entreelementos discretos.

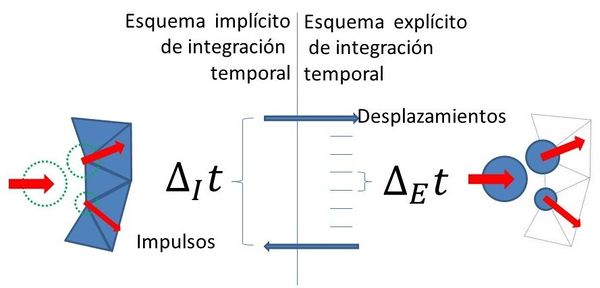
La implementación para el estudio de problemas transitorios seguida en esta investigación corresponde a un esquema de integración temporal de sub-etapas en el cual los elementos finitos se calculan mediante un esquema implícito de Newmark y los elementos discretos mediante un esquema explícito de diferencias centradas. Normalmente el incremento de tiempo del esquema implícito suele ser 100 veces mayor que el explícito.

La ventaja de esta estrategia es en que el número de elementos discretos suele ser mucho menor que el de elementos finitos que discretizan la estructura, por lo que la integración explícita realizada dentro de un paso de tiempo implícito es bastante rápida. Antes de comenzar un nuevo paso de tiempo ${\textstyle {\Delta }_{I}t}$ en el esquema implícito, se calcula el mismo período de tiempo con un esquema explícito sobre los elementos discretos usando un incremento de tiempo ${\textstyle {\Delta }_{E}t}$.

El contacto entre elementos discretos se cuantifica por la suma de los impulsos que se producen a lo largo del análisis explícito y se expresa como una fuerza sobre los elementos discretos, aplicada en el tiempo t + 1 correspondiente al esquema implícito tal como se muestra en la Figura 2.

Se ha observado que no es aconsejable que los intervalos de tiempo ${\textstyle {\Delta }_{I}t}$ y ${\textstyle {\Delta }_{E}t}$ tengan una relación mayor que 1: 500 ya que pueden haber discrepancias entre la solución explícita y la implícita. Teniendo esto en cuenta, la estrategia de solución en sub-pasos implementada permite obtener excelentes resultados, como se muestra en los ejemplos del siguiente apartado.

7.- Ejemplos

En este apartado se muestran varios ejemplos a fin de mostrar el buen comportamiento de la estrategia FEM-DEM descrita. El primer ejemplo corresponde al estudio 3D de una probeta normalizada en un ensayo a tracción. El segundo ejemplo es una viga de hormigón bi-entallada donde predomina la fractura en modo mixto. El tercer ejemplo corresponde al ensayo de tracción indirecta, ampliamente usado en mecánica de rocas. El cuarto ejemplo consiste en un ensayo de cortante en hormigón propuesto por Luong [21]. El quinto ejemplo es un ensayo de una probeta a compresión simple. El sexto ejemplo es el estudio de un forjado reticular de hormigón armado, afectado por un asentamiento diferencial. El acero se considera embebido y solidario con los desplazamientos de los elementos finitos utilizados.

Finalmente, se presenta el análisis sísmico de la nave central de la iglesia del monasterio de Poblet , formada por elementos de mampostería, aplicándole un sismo de 6 ${\textstyle {M}_{w}}$. En este ejemplo se puede observar como la estrategia FEM-DEM modela el efecto de la apertura y cierre de múltiples grietas.

7.1 Ensayo normalizado de tracción

El primer ejemplo corresponde al análisis de fractura de una probeta de hormigón sujeta a fuerzas de tracción. El objetivo principal es mostrar la independencia del tamaño de la malla en la generación de la grieta, de manera que la energía utilizada en la fractura sea independiente del tamaño elemental. La geometría se define de acuerdo con la norma D638 de la Sección Norteamericana de la Asociación Internacional de Ensayo de Materiales (ASTM, American Society for Testing and Materials) [22]. En la Figura 3 se muestran las tres mallas de elementos tetraédricos de 4 nodos utilizadas, así como las condiciones de contorno. La probeta se carga imponiendo un campo de velocidad constante de tracción en sus extremos, representados por la zona oscura en la figura.

El estudio se ha realizado utilizando la metodología FEM-DEM en 3D antes descrita. Con el fin de localizar la fractura, sólo se permite que una banda de elementos se rompa al nivel de la tensión de fallo, usando el modelo de daño mencionado. Los resultados obtenidos se analizan dibujando los desplazamientos de los puntos PA y PB mostrados en la Figura 3.

El módulo de Young, el coeficiente de Poisson y la densidad son respectivamente ${\textstyle {E}_{0}}$ = 30 × 10⁹Pa, ${\textstyle \nu }$ = 0.2, ${\textstyle \gamma }$ = 1.0 × 10³ N/m³, la tensión máxima de tracción ${\textstyle {\sigma }_{f}}$ = 10 × 10³Pa y la energía de fractura G = 7.5 × 10^-3 J/m².

La probeta se deforma aplicando una velocidad constante de tracción de 0.5×10^-7 m/s en ambos extremos . La Figura 4 muestra la geometría dañada para las tres mallas del FEM consideradas.

Obsérvese que cuando se produce una fractura, se crean elementos discretos en los labios de la única fisura que aparece en este ejemplo, como se explica en los apartados anteriores. El tamaño de las esferas no es uniforme debido a que no todos los elementos llegan al daño máximo de manera simultánea.

Con objeto de evaluar la apertura de la grieta se analiza el desplazamiento de los puntos PA y PB situados a la derecha y en el centro de la probeta, respectivamente (Figura 3). La Figura 5 muestra la relación carga-desplazamiento en estos puntos. Para las tres mallas consideradas la evolución del desplazamiento es muy similar y de acuerdo con los resultados esperados [9]. Debido a que los elementos por donde se abre la grieta tienen un tamaño diferente para cada malla, el desplazamiento del punto PB en la región elástica se hace más pequeño a medida que se reduce el tamaño del elemento.

7.2 Viga bi-entallada a flexión.

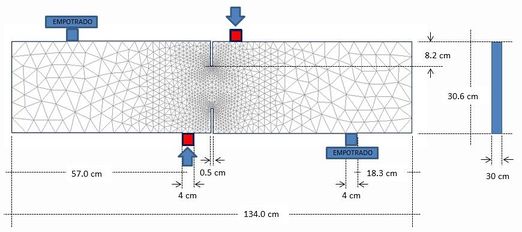
El siguiente ejemplo corresponde al ensayo de una viga de hormigón en masa bi-entallada. El análisis se realiza mediante las hipótesis de tensión plana y es un buen ejemplo de fractura en modo mixto. La viga se sostiene en dos puntos y se somete a flexión aplicando un desplazamiento impuesto mediante control de velocidad equivalente a 1 mm/s en los dos puntos representados en la Figura 6. Igualmente, en dicha figura también se muestran la geometría y las dimensiones de la probeta.

La viga presenta dos puntos singulares en la punta de las dos entallas en donde las tensiones de tracción son altas y el daño comienza en esta zona. Las propiedades del material son ${\textstyle {E}_{0}}$ = 30 × 10⁹Pa, ${\textstyle \nu }$ = 0.2, ${\textstyle {\sigma }_{f}}$ = 2 MPa y G= 1 × 10² J/m². El problema ha sido resuelto con la técnica FEM-DEM en 2D.

En la Figura 7 se muestra un detalle de las tres diferentes mallas utilizadas, formadas por 1165 nodos y 2202 elementos triangulares lineales para la malla gruesa, 1847 nodos y 3480 elementos para la malla intermedia y 5747 nodos y 11206 elementos para la malla fina. El análisis se ha realizado tanto forma cuasiestática como de forma dinámica, respetando la velocidad de aplicación de la carga. En ambos casos los resultados han sido muy similares como se observa en la Figura 9.

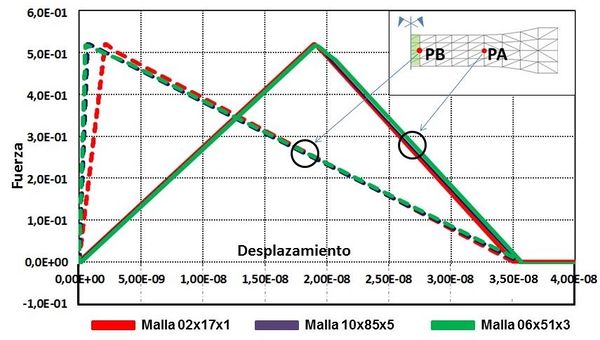
La Figura 8 muestra la dirección de las fisuras para las tres mallas analizadas las cuales coinciden con los experimentos numéricos [14]. La Figura 9 muestra la relación entre la reacción y el desplazamiento impuesto en cualquiera de los dos puntos representados en la figura 6 (los resultados son idénticos para los dos puntos). Los gráficos son concordantes con los resultados obtenidos por Cervera et. al. [14].

7.3 Ensayo de tracción indirecta

El ensayo brasileño de tracción indirecta (BTS, de Brazilian Tensile Strength) es un procedimiento sencillo para evaluar la resistencia a la tracción de hormigón y geomateriales. La probeta de hormigón analizada es un cilindro de 0.2m de diámetro (D) y 0.1m de espesor (t), sujeto a una carga diametralmente opuesta (Figura 10). El valor de la resistencia a la tracción se calcula mediante la siguiente expresión [23, 24].

donde P es el valor de la carga aplicada. Las propiedades del material son ${\textstyle {E}_{0}}$ = 21 × 10⁹Pa, ${\textstyle \nu }$ = 0.2, ${\textstyle \gamma }$ = 7.8 × 10³N/m³, ${\textstyle {\sigma }_{f}}$ = 10 KPa y G= 1 × 10² J/m². Lo que proporciona una carga máxima de fallo de P = 314.16 N.

Para realizar los análisis se han usado tres mallas de 9338, 31455 y 61623 elementos tetraédricos lineales como se muestra en la Figura 10. El ensayo se realiza imponiendo una velocidad constante vertical en la parte superior de la probeta.

La Figura 11 muestra la grieta y los elementos discretos generados. Se puede observar que el patrón de fisuración es similar para las tres mallas y de acuerdo con el resultado esperado. La Figura 12 muestra la curva de carga-desplazamiento. Los valores obtenidos para la resistencia a la tracción máxima para las mallas gruesa, media y fina son respectivamente: 10.693 KPa, 10.351 KPa y 10.235 KPa, correspondientes a un rango de entre 6% y 2% de error frente al valor esperado de ${\textstyle {\sigma }_{f}}$ = 10 KPa.

Es remarcable la insensibilidad de la curva carga-desplazamiento al tipo de malla de elementos finitos utilizada. Esta “objetividad” de los resultados numéricos frente al tamaño de la malla del FEM es una de las características esenciales de la técnica FEM-DEM.

7.4 Ensayo de cortante

El ensayo de cortante se diseña para aplicar un esfuerzo de cizalladura sobre una probeta de modo que experimente una falla por deslizamiento a lo largo de un plano paralelo a las fuerzas aplicadas. Por lo general las fuerzas de cizallamiento provocan que una de las superficies de fallo de un material se mueva en una dirección y la otra superficie en dirección opuesta, de manera que el material se encuentra sometido a un estado de corte. Este ejemplo se realizó en 80 minutos usando un procesador a 2.5 MHz

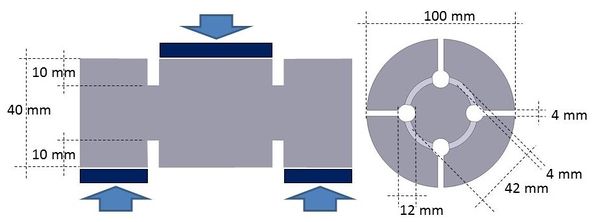
El ensayo que aquí se considera tiene como objetivo determinar la resistencia a cortante del hormigón y ha sido propuesto por Luong [21]. La probeta tiene forma tubular y su eje coincide con el eje z = 0. Tiene varias entallas y se somete a una carga central en una de sus caras y otra excéntrica en la cara opuesta, de manera que se generen tensiones cortantes paralelas al eje z = 0, como se describe en la Figura 13 en la que también se muestran las condiciones de contorno impuestas. La profundidad de la entalla es de 10mm y su ancho es de 4mm. La carga se aplica imponiendo a la placa superior una velocidad constante de 1mm/s hasta llegar a la fractura.

La definición geométrica y la malla de elementos finitos utilizada se muestran en la Figura 14. El plano de cizallamiento ha sido discretizado con 4 elementos finitos tetraédricos de 4 nodos con el fin de captar adecuadamente el gradiente de tensiones en esta zona.

Las propiedades del hormigón son ${\textstyle {E}_{0}}$ = 35 × 10⁹Pa, ${\textstyle \nu }$ = 0.22, ${\textstyle \gamma }$ = 7.8 × 10³ N/m³, ${\textstyle {\sigma }_{c}}$ = 30 MPa, ${\textstyle {\sigma }_{f}}$ = 3 MPa y G = 75 × 10^-3 J/m². En general el esfuerzo máximo de corte en el hormigón es aproximadamente 1/5 o 1/6 del esfuerzo a compresión [21].

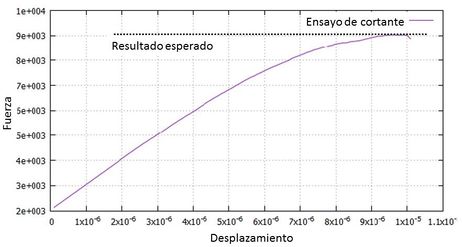
La Figura 15 muestra la grieta obtenida por el experimento numérico con la técnica FEM-DEM y se compara con los resultados de los ensayos realizados en el laboratorio. La Figura 16 muestra la relación fuerza-desplazamiento obtenida numéricamente y en la que se muestra claramente la rama elástica hasta que los elementos comienzan a dañar. Considerando el tamaño de la probeta, de esta gráfica se desprende que el esfuerzo cortante último alcanza un valor de 5.10 MPa. Este resultado es coherente y próximo al valor esperado [21].

7.5 Ensayo de compresión simple

Uno de los ensayos más frecuentes realizados en probetas de hormigón es el de compresión simple [25]. El ensayo se realiza de acuerdo con la instrucción de hormigón estructural (EHE-08) [26] la cual hace referencia a la norma UNE-EN 12390-3.2009 [27] en donde se especifica las dimensiones de las probetas y las condiciones de ensayo.

El experimento numérico que se presenta se realiza en 2D utilizando probetas hexaédricas en tensión plana y para el caso 3D probetas cilíndricas normalizadas.

El ensayo 2D consiste en comprimir la probeta cuyas dimensiones y condiciones de carga se muestra en la Figura 17 y en la cual también se presentan las mallas utilizadas. El objetivo del ensayo no solo se trata de encontrar la tensión máxima a compresión que es capaz de resistir la probeta sino también la forma de las fisuras en función de las distintas condiciones de contorno que se pueden dar en el ensayo.

Las propiedades del hormigón utilizadas son. ${\textstyle {E}_{0}}$ = 30.0 × 10⁹Pa, ${\textstyle \nu }$ = 0.20, ${\textstyle \gamma }$ = 24 × 10³N/m³, ${\textstyle \,{\sigma }_{c}}$ = 2000 MPa, ${\textstyle {\sigma }_{t}}$= 20.0 MPa y G = 105 × 10^-3 J/m² En este caso la tensión máxima de compresión, independientemente de las condiciones de apoyo es de 20 × 10⁶Pa. En la Figura 18 se muestra que los resultados obtenidos con ambas probetas se acercan mucho al resultado esperado.

Los resultados más interesantes en este caso se muestran en las Figuras 19 a 21. En todas ellas la figura a) corresponde al patrón de grietas generado, la b) son las superficies de igual desplazamiento y la figura c) el daño elemental. Estos resultados se pueden comparar con la figura d) que corresponde a los resultados teóricos [28] o bien con la figura e) que corresponde a los resultados obtenidos con LS-DYNA [29] para el caso bi-empotrado (Figuras 19 y 20) o con un ensayo real (Figura 21)

La Figura 19 corresponde al caso en que las superficies de carga tienen un desplazamiento horizontal nulo utilizando la malla de elementos finitos estructurada. Los resultados muestras claramente dos grietas a 45º claramente definidas, y corroboradas por el patrón de daño mostrado. El resultado numérico mostrado en la figura e) muestra el mismo patrón. Sin embargo, observando los resultados teóricos [28] el daño se genera sobre dos bandas a 45º formadas por grietas verticales.

La Figura 20 muestra el mismo caso, con el desplazamiento horizontal de las superficies de carga impedidas, pero utilizando la malla no estructurada. Como se puede observar en la Figura 20 a) el patrón de grietas se asemeja más a los resultados teóricos esperados, con grietas verticales localizadas en dos bandas a 45º. Es importante mencionar que ningún código numérico al que los autores han tenido acceso es capaz de presentar este tipo de resultados, pues todos muestran correctamente la banda de daño (Figura e) pero no así las fisuras verticales sobre dicha banda. El por qué la malla no estructurada presenta un resultado más próximo al teórico está relacionado con la no uniformidad en la discretización de dominio. Las pequeñas variaciones numéricas inducidas por los elementos de distinto tamaño son suficientes para alterar la estabilidad de los resultados que se obtienen con una malla estructurada, encontrado así un resultado diferente.

La Figura 21 presenta los resultados obtenidos con la malla no estructurada en el caso en qué las superficies de carga tengan libertad de movimiento horizontal. Teóricamente [28], como se muestra en la Figura 21 d), la fisura debe ser vertical, sin embargo, como se observa en la Figura 21 e), los ensayos de laboratorio tienden a presentar varias fisuras verticales [27]. Los resultados mostrados en la Figura 21 a) concuerdan con los resultados esperados.

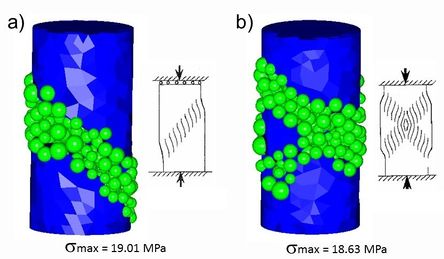
El mismo ejemplo ha sido resuelto en 3D utilizando una probeta circular (Figura 17) y las mismas propiedades mecánicas. La malla está formada por 926 nodos y 4030 tetraedros. Los resultados obtenidos se muestran en la Figura 22 a) para el caso en que una de las superficies de carga se encuentre impedida en su desplazamiento horizontal, mientras que la otra no. La Figura 22 b) muestra el caso en que ambas superficies tengan el desplazamiento horizontal impedido. En ambos ejemplos la tensión máxima se aproxima bastante a la esperada. No solo eso, a pesar que la malla sea tan gruesa, las grietas generadas coinciden con los resultados teóricos. Cabe comentar que este ejemplo no requiere más de 5 minutos de cálculo en un procesador a 2.5 GHz.

7.6 Losa reticular

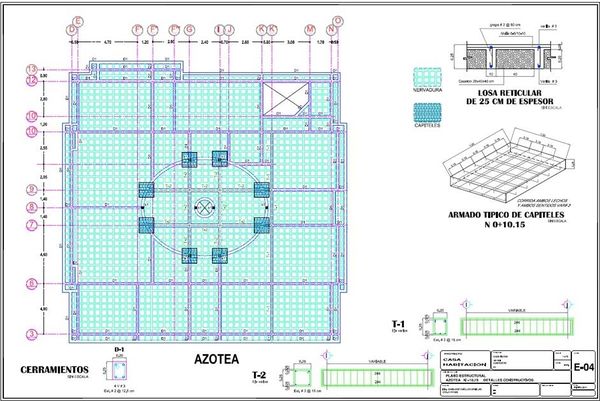
El uso de forjados reticulares como elementos estructurales está ampliamente consensuado y permite construir geometrías arquitectónicas más libres. El forjado analizado corresponde al techo de una vivienda. La planta es un cuadrado de 22m de lado con una superficie plana ovalada en el centro y los lados en parteaguas con un desnivel de 2m. En la Figura 23 se muestra la planta estructural en donde se puede observar claramente la armadura de acero. Básicamente se trata de un forjado reticular de 0.25m de espesor con una capa de compresión de 0.05m y casetones de 0.40 × 0.40 × 0.20m. A lo largo de las nervaduras se colocan varillas de acero del No. 3 (ϕ = 0.0095m).

Adicionalmente existe una serie de cerramientos (D1) y vigas (T1 y T2) así como cuatro capiteles de columna. Los cerramientos tienen una sección de 0.25 × 0.20m armados con 4 varillas de acero del No. 3. Las vigas T1 y T2 tienen un espesor de 0.25m y un ancho de 0.20m para la viga T1 y de 0.25m para la viga T2. Ambas están armadas con 4 varillas de acero del No. 4 (ϕ = 0.0127m). Finalmente, el armado de los capiteles se realiza con varillas del No. 3 @ 0.15m en ambos lechos y en ambas direcciones. La Figura 24 a) muestra el armado de toda la losa, así como un detalle del armado de los capiteles en la Figura 24 b).

Las propiedades del hormigón son. ${\textstyle {E}_{0}}$ = 21 × 10⁹Pa, ${\textstyle \nu }$ = 0.20, ${\textstyle \gamma }$ = 24 × 10³ N/m³, ${\textstyle {\sigma }_{c}}$= 20 MPa, ${\textstyle {\sigma }_{f}}$= 2 MPa y G = 100 × 10^-3 J/m².

La placa se encuentra apoyada sobre los muros mostrados en la Figura 25. A efectos del análisis dichos muros se consideran lo suficientemente rígidos y empotrados en su base.

Las cargas consideradas son el peso propio de la estructura, las cargas muertas 1620 N/m² y las cargas vivas 400 N/m². Dichos valores consideran el peso del plafón, las instalaciones y acabados finales, sin considerar cargas de nieve o viento. Adicionalmente se impone un asentamiento diferencial de 0.0035 m de los puntos de la base del muro como se indica en la Figura 25.

El problema se ha resuelto utilizando una malla de 1,369,192 tetraedros y 368,969 nodos. Por otra parte, se han definido 5,084 elementos lineales para representar las varillas de acero. La Figura 26 a) representa el conjunto del forjado y muros a analizar mientras que la Figura 26 b) corresponde a un detalle cercano al lucernario donde se aprecian las nervaduras de la placa, así como algunas de las vigas T2.

la Figura 27 a) muestra los resultados del desplazamiento de la estructura después de que el asentamiento diferencial de la base sea de 0.0035 m. En la Figura 27 b) se aprecia un corte muy definido en la cubierta superior. Se observa que el desgarro en la cubierta es perpendicular a la dirección del muro, poniendo de manifiesto la gran rigidez que tiene la cubierta superior.

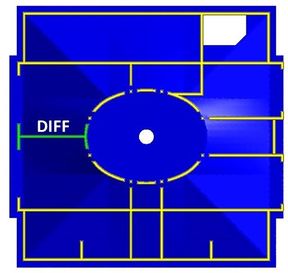
En la Figura 28 a) se puede apreciar la deformada de la estructura vista desde abajo. Es interesante observar que el lucernario sufre los desplazamientos máximos, incluso mayores a los que sufre el muro sujeto al asentamiento diferencial. La Figura 28 b) muestra una vista inferior de la losa donde se aprecia el daño producido en la unión del muro con ésta.

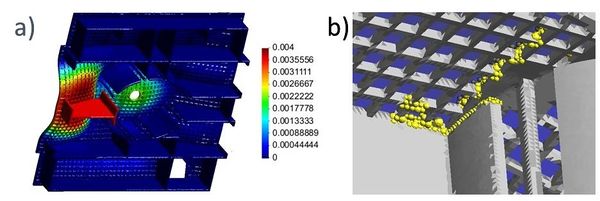
En la Figura 29 se observan los esfuerzos axiales sobre los elementos de acero pertenecientes a la viga T2 en la zona cercana al lucernario. En esta figura se puede observar los elementos en tracción y compresión debido a gran flexión a la que está sujeta esta parte de la estructura.

La Figura 30 muestra las zonas dañadas de la estructura utilizando una visualización de la estructura deformada con un factor de escala de 5000. El recuadro a) muestra una vista inferior de la losa en donde se puede observar la separación entre el muro y la losa, mientras que el recuadro b) muestra una vista superior mostrando el desgarro de la cubierta. En vista de los resultados obtenidos es claramente notorio la gran rigidez que posee la losa

7.7 Iglesia cisterciense del monasterio de Poblet

La iglesia, perteneciente al Real Monasterio de Santa Maria de Poblet, ubicado en Vimbod (Tarragona), es un monumento histórico artístico declarado por la UNESCO como patrimonio de la humanidad. Construido a partir de la segunda mitad del siglo XII, el templo adopta una planta basilical orientado su ábside al Este. La integran tres naves de siete tramos, con crucero, ábside central, girola y capillas absidiales. La nave central tiene unas dimensiones de 85m de longitud, 21m de anchura y 28m de altura, mientras que las laterales alcanzan los 18m de altura. La diferencia de altura respecto a la nave central no se resuelve mediante arbotantes del estilo gótico, sino con contrafuertes. La nave central plenamente románica, está cubierta con bóveda de cañón apuntada, con arcos fajones en cada tramo como se muestra en la Figura 31.

Para simplificar el estudio se analiza únicamente una sección de la nave central que se considera simétrica respecto al eje normal a la dirección de dicha nave. La malla que discretiza la iglesia tiene 9294 nodos y 32487 elementos tetraédricos de cuatro nodos como se muestra en la Figura 32 a). Las propiedades del material utilizado se corresponden con una piedra caliza propia de la región, con ${\textstyle {E}_{0}}$ = 35 × 10⁹Pa, ${\textstyle \nu }$ = 0.22, ${\textstyle \gamma }$ = 25 × 103 N/m³, ${\textstyle {\sigma }_{c}}$ = 780 MPa, ${\textstyle {\sigma }_{f}}$ = 5 MPa y G = 100 × 10^-3 J/m². En cuanto a las condiciones de apoyo, se considera empotrada toda la superficie inferior del modelo.

Las cargas aplicadas corresponden a un movimiento oscilatorio impuesto en dirección normal al eje de la nave central, como se muestra en la Figura 32 b). Los valores mostrados corresponden al movimiento oscilatorio en dirección S 00E de los registros en desplazamientos obtenidos del acelerograma del sismo “El Centro” del 18 de mayo de 1940 [30]. Estos valores se aplican al modelo con una reducción del 50%, de forma que simule un sismo de magnitud6.0 M_W.

Aunque el registro de movimientos dura más de 50 segundos la estructura solo es capaz de soportar en pie 4 segundos, colapsando de forma total a partir de ese instante. En la Figura 33 se observa a intervalos de un segundo las grietas formadas en la Iglesia. Inicialmente ocurre un cizallamiento de las columnas y de la pared más rígida, para posteriormente, cortar las bases de los arcos. A partir del segundo cinco se observa como la estructura colapsa en su totalidad reduciéndose a escombros.

Este ejemplo muestra claramente la capacidad de la técnica FEM-DEM para simular la aparición y propagación de múltiples fracturas en estructuras de mampostería, así como el eventual colapso de la estructura bajo cargas dinámicas.

8.- Conclusiones

Se ha descrito en el presente artículo las líneas generales de la metodología FEM-DEM propuesta por los autores en [9, 10] para la predicción de la aparición y evolución de fisuras en estructuras de hormigón. Los ejemplos que se han presentado muestran las posibilidades de la técnica FEM-DEM para el cálculo no lineal de estructuras de hormigón en masa y armado, así como en estructuras de mampostería. La técnica FEM-DEM es también aplicable al estudio de la fractura en macizos rocosos [31, 32].

9.- Agradecimientos

Los autores agradecen la colaboración del Ing. Juan José Cuellar Ornelas al facilitar de forma desinteresada la información usada en el análisis del forjado. Los resultados aquí presentados han sido obtenidos utilizando los programas FEM2DEM y DEMPACK ([http http].//www.cimne.com/dempack) en los que se ha implementado la metodología FEM-DEM descrita.

REFERENCES

[1] P. A. Cundall and O. D. L. Strack, A discrete numerical model for granular assemblies, Geotechnique 29 (1979), no. 1, 47 –65.

[2] C. Labra, Advances in the development of the discrete element method for excavation processes, Ph.D. Thesis, Barcelona, 2012.

[3] J. Rojek, E.. Oñate, F. Zarate, and J. Miquel, Modelling of rock, soil and granular materials using spherical elements, 2nd European Conference on Computational Mechanics ECCM- 2001, Cracow (2629 June 2001).

[4] J. Williams and R. O’Connor, Discrete element simulation and contact problem, Archives of Computer Methods in Engineering 6 (1999), no. 4, 279 –304.

[5] E. Oñate, F. Zárate, J. Miquel, M. Santasusana, M.A. Celigueta, F. Arrufat, R. Gandijota, K. Valiullin, and L. Ring, A local constitutive model for the discrete element method. Application to geomaterials and concrete, Computational Particle Mechanics 2 (2015), 139–160.

[6] S. Katagiri and S. Takada, Development of fem-dem combined method for fracture analysis of a continuos media, Memoirs of the Graduate School of Science and Technology, Kobe University Japan. 20A (2002 –03), 65 –79.

[7] A. Munjiza, The combined finite-discrete element method, isbn 0-470-84199-0, Wiley, 2004.

[8] Shmauder S. Wulf J. and Fischmeister H.F., Finite element modelling of crack propagation in ductile fracture, Computation Materials Science 1 (1993), 297 –301.

[9] F. Zárate and E. Oñate, A simple FEM-DEM technique for fracture prediction in materials and structures, Computational particle mechanics 2 (2015), no. 3, 301–314.

[10] F. Zárate, A. Cornejo, and E. Oñate, A three-dimensional FEM-DEM technique for predicting the evolution of fracture in geomaterials and concrete, Computational particle mechanics (2017), DOI 10.1007/s40571-017-0178-z

[11] E. Oñate. Cálculo de estructuras por el método de elementos finitos. Análisis estático lineal. Vol. 1 Sólidos (CIMNE, 2017, en castellano); Vol 2. Placas y láminas (Springer 2009, en inglés)

[12] M. Cervera, M. Chiumenti, and C. Agelet de Saracibar, Shear band localization via local j2 continuum damage mechanics, Comput. Methods Appl. Mech. Engrg. 193 (2004), 849 –880.

[13] M. Cervera, M. Chiumenti, and R. Codina, Mixed stabilized finite element methods in nonlinear solid mechanic’s part I. Formulation., Computer Methods in Applied Mechanics and Engineering 199 (2010), 2559 –2570.

[14] M. Cervera, M. Chiumenti, and R. Codina, Mesh objective modelling of cracks using continuous linear strain and displacements interpolations, Int. J. Numer. Meth. Engng. 87 (2011), 962 –987.

[15] P.R. Johnson, N. Petrinic, and E. Sli, Element –splitting for simulation of fracture in 3d solid continua, VIII International Conference on Computational Plasticity, Barcelona. (2005).

[16] L. Mishnaevsky Jr, N. Lippmann, and S.; Schmauder, Computational modelling of crack propagation in real microstructures of steels and virtual testing of artificially designed materials, International Journal of Fracture 120 (2003), 581 –600.

[17] J. Lopez, S. Oller, E. Oñate, and J. Lubliner, A homogeneous constitutive model for masonry, Int. J. Numer. Meth. Engng. 46 (1999), 16511671.

[18] O.C Zienkiewicz and J.Z. Zhu, The superconvergent patch recovery (spr) and adaptive finite element refinement., Comput. Methods App. Mech. Engng. 101 (1992), 207 –224.

[19] E. Oñate “Desarrollos y aplicaciones de modelos de fractura en la Escuela de Ingenieros de Caminos de Barcelona”, Centro Internacional de Métodos Numéricos en Ingeniería, CIMNE (2000).

[20] C. Labra and E. Oñate, High-density sphere packing for discrete element method simulations, Commun. Numer. Meth. Engng. 25 (2009), no. 7, 837 –849.

[21] M. Luong, Tensile and shear strengths of concrete and rock, Engineering Fracture Mechanics 1-3 (1990), no. 35, 127–135.

[22] Astm standard d638 - 10, 2003, “standard test method for tensile properties of plastics,” astm international, west Conshohocken, PA, 2003, doi. 10.1520/d0638-10, www.astm.org.

[23] F. L. L. B. Carneiro, A new method to determine the tensile strength of concrete, Proceedings of the 5th meeting of the brazilian association for technical rules., 1943, pp. 126 –129. (In Portuguese).

[24] C.G. Rocco, G.V. Guinea Tortuero, J. Planas Roselló y M. Elices Calafat. Efecto del tamaño de probeta sobre la resistencia a la tracción medida con el ensayo brasileño. Hormigón y acero 204 (1997), 47-63

[25] J. Rodríguez del Viso, J.R. Carmona y G. Ruiz López. Efecto de la forma y el tamaño de la probeta en la resistencia a compresión en hormigón de alta resistencia. Hormigón y Acero 248 (2008), 77-86

[26] Norma a Instrucción de Hormigón Estructural (EHE-08) https.//www.fomento.gob.es/MFOM/LANG_CASTELLANO/ORGANOS_COLEGIADOS/MASORGANOS/CPH/instrucciones/EHE_es/

[27] UNE-EN 12390-3.2009 Ensayos de hormigón endurecido. Parte 3. Determinación de la resistencia a compresión de probetas. (2009) Asociación Española de Normalización y Certificación AENOR

[28] Z. P. Bazant, J. Planas, Fracture and Size Effect in Concrete and Other Quasibrittle Materials CRC Press LLC (1998). ISBN 9780849382840

[29] Y.D. Murray, A Abu-Odeh and R. Bligh., Evaluation of LS-DYNA Concrete Material Model 159 Publication No. FHWA-HRT-05-063, (2007) US Department of Transportation.

[30] Ground accelerogram from el-centro, imperial valley irrigation district (comp s00e). http.//www.eng.ucy.ac.cy/petros/earthquakes/eq1.txt.

[31] J. M. González, F. Zárate, E. Oñate Pulse fracture simulation in shale rock reservoirs: DEM and FEM–DEM approaches. Computational particle mechanics Online (2017), 1–17.