Multicolor Parallel Fourth-Order Implicit Finite Difference for Solving the 2D Poisson Equation

Abstract

The Poisson equation is central in numerous physics and engineering applications, such as computational fluid dynamics and acoustic wave propagation, where efficient and accurate solutions are essential. This study focuses on the numerical solution of the 2D Poisson equation with Dirichlet boundary conditions using a fourth-order compact Implicit Finite Difference scheme. Finite difference methods, particularly high-order schemes, are advantageous for solving the Poisson equation due to their efficiency and suitability for structured grids. To address the computational demands of large-scale problems, we incorporate domain decomposition and the Multicolor Successive Over Relaxation method, facilitating parallel computation. Through numerical experiments, we demonstrate that our approach significantly enhances both accuracy and computational efficiency when compared to traditional second-order methods.

keywords

Fourth-order finite difference, Domain decomposition, MPI, Poisson equation, Speedup, Elapsed time

1 Introduction

The Poisson equation plays a crucial role in a wide range of physics and engineering applications, including computational fluid dynamics, acoustic wave propagation, and theoretical physics [1]. However, the implementation of simple, accurate, and efficient numerical solver remains fundamental to the successful resolution of these problems. In this work, we study the numerical solution of the 2D Poisson equation, which is formulated as follows:

$u_{xx}(x,y)+u_{yy}(x,y)=f(x,y),\;\;(x,y)\in \Omega ,$

(1)

where ${\textstyle \Omega =({\mathfrak {a}},{\mathfrak {b}})\times ({\mathfrak {c}},{\mathfrak {d}})}$ and Dirichlet boundary conditions are applied on ${\textstyle \partial \Omega }$. The right-hand side ${\textstyle f}$ is a know function defined over ${\textstyle \Omega }$. The study of large-scale physical phenomena, which often involves solving Poisson's equation (1), requires significant computational effort. As a result, these computations demand parallel computing systems with high-speed, massively parallel processors and large memory capacities to efficiently implement numerical approaches within this framework [2]. Domain decomposition is a popular strategy for dividing the overall problem into smaller sub-domain problems, where parallelization can be effectively applied [3]. This technique offers advantages such as simpler construction and greater speed-up. Many numerical methods have been developed to exploit these benefits. However, finite difference (FD) methods are preferred for solving the Poisson equation over rectangular domains, as they typically lead to a large, block-structured, and sparse system of equations [4]. In addition, for smooth problems, high-order FD methods can compute numerical solutions hundreds of times faster than second-order FD schemes for a fixed level of accuracy. Implicit finite difference (IFD) methods provide high-order schemes without the drawback of requiring large stencils; in fact, some of them are associated with compact schemes [5].

In this paper, we present a compact implicit finite difference (IFD) scheme for numerically solving the 2D Poisson problem, which is primarily based on the domain decomposition strategy. Furthermore, the Successive Over-Relaxation (SOR) method is chosen for its efficiency and simplicity as a solver. However, since SOR is inherently sequential, it cannot be directly parallelized. To address this limitation, a coloring method is employed, as suggested in previous works [6,7,8,9].

This paper is organized as follows: Section 2 provides the high-order finite difference discretization. Section 3 is devoted to explaining the domain decomposition technique. In Section 4, we test our algorithm with several numerical examples and evaluate its speedup and efficiency. Finally, Section 5 presents the conclusions and suggestions for future work.

2 Fourth-order Implicit Finite Difference Scheme

The classic one-dimensional finite-difference approximation for a second derivative of a real-valued function ${\textstyle \phi }$ at ${\textstyle x}$ with a small value ${\textstyle h>0}$ is given by

$\delta ^{2}\phi ={\frac {\phi (x+h)-2\phi (x)+\phi (x-h)}{h^{2}}}.$

(2)

Using Taylor series, it follows that the second-order derivative at ${\textstyle x}$ can be approximated by (2) with the following local truncation error

$\phi _{xx}={\frac {\phi (x+h)-2\phi (x)+\phi (x-h)}{h^{2}}}-{\frac {1}{12}}h^{2}\phi _{xxxx}-{\frac {1}{360}}h^{4}\phi _{xxxxxx}+h.o.t.$

(3)

Note that the accuracy of centered finite difference approximation (3) can be fourth-order re-arranging the terms as follows

$\phi _{xx}+bh^{2}\left(\phi _{xx}\right)_{xx}={\frac {\phi (x+h)-2\phi (x)+\phi (x-h)}{h^{2}}}+O(h^{4}),$

(4)

where ${\textstyle b=1/12}$. Furthermore, it can be shown that the second-order derivative operator ${\textstyle (\cdot )_{xx}}$ on the left-hand side can be replaced by a finite difference operator ${\textstyle \delta ^{2}}$ without compromising the overall order of accuracy [5], as follows

$\left(1+bh^{2}\delta ^{2}\right)\phi _{xx}=\delta ^{2}\phi +O(h^{4}).$

(5)

This formulation is called implicit because approximations to the second-order derivative appear in both sides of equation (5). Finally, we remark that the application of the implicit operator for a general real-valued function ${\textstyle u}$ (in particular ${\textstyle u=\phi _{xx}}$) is given by

${\mathfrak {D}}u=\left(1+bh^{2}\delta ^{2}\right)u=bu(x+h)+(1-2b)u(x)+bu(x-h).$

(6)

2.1 Two-dimensional scheme

In this section, we present the numerical scheme for solving the 2D Poisson problem. The computational domain, ${\textstyle \Omega }$, is divided using a uniform mesh with ${\textstyle N}$ sub-divisions along the ${\textstyle x}$- and ${\textstyle y}$-axes, where the grid points are defined as follows:

$x_{i}={\mathfrak {a}}+h_{x}i,\quad i=0,1,2\dots ,N_{x},$ (7) $y_{j}={\mathfrak {c}}+h_{y}j,\quad j=0,1,2\dots ,N_{y},$ (8)

where ${\textstyle h_{x}=({\mathfrak {b}}-{\mathfrak {a}})/N_{x}}$ and ${\textstyle h_{y}=({\mathfrak {d}}-{\mathfrak {c}})/N_{y}}$. To maintain a simple explanation, we assume that the computational domain is a square, so ${\textstyle N=N_{x}=N_{y}}$ and ${\textstyle h=h_{x}=h_{y}}$. We use the following notation: ${\textstyle u_{i,j}=u(x_{i},y_{j})}$ and ${\textstyle f_{i,j}=f(x_{i},y_{j})}$ where ${\textstyle (x_{i},y_{j})}$ represents the ${\textstyle ij}$-th grid point.

Let us consider the finite difference operators

${\mathfrak {D}}_{x}=1+b\delta _{x}^{2},\qquad \mathrm {and} \qquad {\mathfrak {D}}_{y}=1+b\delta _{y}^{2}.$

(9)

The subscripts at ${\textstyle {\mathfrak {D}}}$ are not derivatives, they only indicate the dependence of the ${\textstyle x}$ and ${\textstyle y}$ direction respectively. Applying simultaneously these operators at equation (1), it yields

${\mathfrak {D}}_{y}{\mathfrak {D}}_{x}(u_{xx})_{ij}+{\mathfrak {D}}_{y}{\mathfrak {D}}_{x}(u_{yy})_{ij}={\mathfrak {D}}_{x}{\mathfrak {D}}_{y}f_{ij},$

(10)

Next, we use formula (5) to the second derivatives in ${\textstyle x}$ and ${\textstyle y}$ to get

${\mathfrak {D}}_{y}\left({\frac {u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{h^{2}}}\right)+{\mathfrak {D}}_{x}\left({\frac {u_{i,j+1}-2u_{ij}+u_{i,j-1}}{h^{2}}}\right)={\mathfrak {D}}_{x}{\mathfrak {D}}_{y}f_{ij}+O(h^{4})$

(11)

Thus the two-dimensional fourth-order implicit finite difference scheme (IFD) results from applying (6) in 11. The following theorem states the final numerical discretization for 2D Poisson problem using the IFD method.

Theorem 1: Let us assume that the solution ${\textstyle u}$ has sufficient regularity and the grid size ${\textstyle h}$ is positive. The full discretization of the problem (1) is given by the fourth-order scheme

$2b(U_{i-1,j+1}+U_{i+1,j+1}+U_{i+1,j-1}+U_{i+1,j-1})+$ $(1-4b)(U_{i,j-1}+U_{i,j+1}+U_{i-1,j}+U_{i+1,j})+(-4+8b)U_{i,j}=F_{i,j},$

(12)

where

$F_{i,j}=h^{2}\left[(1-4b)f_{i,j}+b(f_{i,j-1}+f_{i,j-1}+f_{i-1,j}+f_{i+1,j})\right],$

(13)

and ${\textstyle U_{i,j}}$ is an approximation of ${\textstyle u_{i,j}}$. More details about the proof of the Theorem 1 can be found in [5]. Additionally, if we set ${\textstyle b=0}$ in (12) the resulting scheme becomes the classical second-order method. This parameter ${\textstyle b}$ allows us directly compare both numerical schemes by setting it either ${\textstyle 0}$ or ${\textstyle 1/12}$. Furthermore scheme (12) is compact scheme because its stencil requires only the surrounding nine points. The stencil of the classical second-order and the fourth-order implicit finite-difference schemes are illustrated in Figure 1.

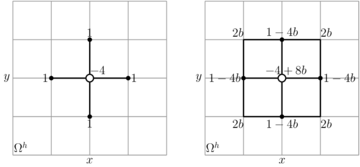
Figure 1: Second- and fourth-order finite-difference stencil for the two-dimensional Poisson equation. The numbers correspond to the weights next to unknown variables.

2.2 Linear system and solvers

The discretization given in (12) and (13) results in large linear system ${\textstyle \mathbf {AU} =\mathbf {F} }$ as ${\textstyle N}$ becomes larger. Therefore, to efficiently obtain the solution ${\textstyle U_{i,j}}$, this system should be solved using an appropiate high-performance numerical solver. It is not difficult to demonstrate that ${\textstyle \mathbf {A} }$ is a diagonally dominant matrix, thus a wide range of iterative linear solvers are available in this case.

Due to their robustness, efficiency and ease of implementation, we consider the classical stationary methods: the Jacobi method, the Gauss-Seidel (GS) method, and the Successive Over-Relaxation (SOR) method [10]. The Jacobi method is a well-known iterative approach that is straightforward to implement and parallelize. However, its slow convergence rate makes it unsuitable for practical, large-scale applications. The GS and SOR methods offer more efficient solvers, with SOR converging faster than GS when an appropriate relaxation factor is chosen. The main challenge with the SOR method is that, in its original form, it cannot be easily parallelized due to its inherently sequential nature. Thus, alternative approaches must be considered for parallel implementation. In this work, we utilize the Multicolor SOR method due to its simplicity in parallelization and its minimal modifications compared to the Jacobi method.

We begin by considering the Jacobi method. While its convergence is slow, it provides the advantages of high execution speed and straightforward implementation, particularly when it comes to vectorization and parallelization. Let the ${\textstyle k}$-th equation of the resulting linear system

$\sum _{l=1}^{N^{2}}a_{kl}\phi _{l}=\ell _{k},$

(14)

then, an iteration of the Jacobi method is given by

$\phi _{k}^{(n+1)}={\frac {1}{a_{kk}}}\left(\ell _{k}-\sum _{\begin{matrix}l=1,l\neq k\end{matrix}}^{N^{2}}a_{kl}\phi _{l}^{(n)}\right),$

(15)

where the ${\textstyle (n+1)}$ values are from the current iteration, and ${\textstyle (n)}$ values are from the previous iteration. Here the vectors ${\textstyle \phi }$ and ${\textstyle \ell }$ are constructed using a natural indexation of matrices ${\textstyle \mathbf {U} }$ and ${\textstyle \mathbf {F} }$, respectively. The iteration process will be stopped once a convergence tolerance ${\textstyle \varepsilon }$ is achieved. Note that the Jacobi method can be easily implemented in parallel since all updated values depend solely on the previous iteration ${\textstyle (n)}$. The convergence rate of the Jacobi method can be improved by employing the SOR method. In these iterative solvers, each component at the new iteration depends on some previously computed components within the same iteration. The SOR method is expressed as:

$\phi _{k}^{(n+1)}=\phi _{k}^{(n)}+\omega \left({\frac {1}{a_{kk}}}\left(\ell _{k}-\sum _{l=1}^{k-1}a_{kl}\phi _{l}^{(n+1)}-\sum _{l=k+1}^{N^{2}}a_{kl}\phi _{l}^{(n)}-a_{kk}\phi _{k}^{(n)}\right)\right),$

(16)

where ${\textstyle 0<\omega {<2}}$ is the relaxation factor. The Gauss-Seidel method is recovered by setting ${\textstyle \omega =1}$ in the SOR method. It is important to note that, unlike the Jacobi method, the computations in the SOR method are inherently sequential, meaning the updates cannot be performed simultaneously.

To apply this solver to our compact fourth-order implicit scheme, we can rewrite (16) but now using a residual vector as follows:

$U_{i,j}^{(n+1)}=U_{i,j}^{(n)}+\omega \left({\dfrac {1}{-4+8b}}R_{i,j}^{(n)}\right),$

(17)

where

$R_{i,j}^{(n)}=F_{i,j}-2b(U_{i-1,j+1}+U_{i+1,j+1}+U_{i+1,j-1}+U_{i+1,j-1})^{(n)}$ $-(1-4b)(U_{i,j-1}+U_{i,j+1}+U_{i-1,j}+U_{i+1,j})^{(n)}-(-4+8b)U_{i,j}^{(n)}.$

(18)

The stopping criterion for (17) with a given tolerance ${\textstyle \varepsilon }$ is that the residual (18) is sufficiently small, i.e., ${\textstyle |R_{i,j}|<\varepsilon }$, for all indices ${\textstyle i,j}$. In addition to the tolerance, we include a maximum number of iterations as a complementary stopping criterion.

2.3 Multicolor SOR method

Several algorithms exist for parallelizing the SOR method on structured grids, and due to their simplicity, coloring methods have often been a popular choice [6]. However, there are limited works on the implementation and performance of these techniques when applied to compact schemes using a nine-point stencil [7,8,9].

The classical two-color SOR method (RBSOR) divides the domain into a chessboard pattern of red and black points. In this configuration, each unknown is updated based on values of the opposite color, allowing the points of the same color to be computed in parallel. However, this algorithm is only applicable to stencils like the classical second-order finite-difference scheme, see Figure 2. Each iteration is carried out in two steps. Updating the first set of points (red) relies solely on previous black values. In contrast, the remaining points (black) require only the already updated red points for their calculations. The challenge with a nine-point stencil lies in the use of corner points, which complicates the direct application of the RBSOR method.

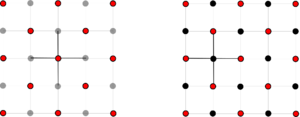
Figure 2: Second-order finite-difference stencil for the two-dimensional Poisson equation using RBSOR iterative method.

In the case of our nine-point compact scheme, four colors are sufficient to decouple the grid points. Thus, the four-color SOR (MCSOR) method is employed. For simplicity, we assign the colors red (R), black (B), green (G), and orange (O). For each grid point of a given color, the nearest grid points along both coordinate directions must be assigned different colors to ensure independence during the update process, as shown in Figure 3. This figure also illustrates the four sub-steps employed to update all grid points for each iteration ${\textstyle (n)}$.

Figure 3: Fourth-order finite-difference stencil for the two-dimensional Poisson equation. The numbers correspond to the weights next to unknown variables.

It is important to remark that we use the same variable to store all color values at each iteration. This approach allows the grid points of each color to be updated using the most recently computed values from the other colors. For example, when updating a reference grid point colored green, the neighboring grid points colored red and black are taken from the current iteration, while the orange values are taken from the previous iteration, as presented below:

$(U_{i,j}^{G})^{(n+1)}=(U_{i,j}^{G})^{(n)}+\omega \left({\dfrac {1}{-4+8b}}R_{i,j}\right),$

(19)

where

$R_{i,j}=F_{i,j}-2b(U_{i-1,j+1}^{O}+U_{i+1,j+1}^{O}+U_{i+1,j-1}^{O}+U_{i+1,j-1}^{O})^{(n)}$ $-(1-4b)(U_{i,j-1}^{R}+U_{i,j+1}^{R}+U_{i-1,j}^{B}+U_{i+1,j}^{B})^{(n+1)}-(-4+8b)(U_{i,j}^{G})^{(n)},$

(20)

and the superscripts in ${\textstyle U}$ indicate the corresponding color. This configuration is expected to lead to faster convergence than the original SOR method, as demonstrated by the numerical results presented in the next section. However, further theoretical investigations are needed in this direction to better understand and confirm the potential improvements in convergence. Finally, we emphasize that, similar to the Jacobi method, the MCSOR method is well-suited to straightforward parallel implementation because all new values only depends on calculations previous sub-steps.

3 Parallelization using domain decomposition

Instead of computing the solution over the entire domain ${\textstyle \Omega }$, we subdivide the domain into smaller parts and compute the solution over each subdomain ${\textstyle \Omega _{k}}$, allowing for parallel computation. Let us define a domain decomposition for the problem using ${\textstyle M}$ strips, as follows

$\Omega =\cup _{k=1}^{M}\Omega _{k},$

where ${\textstyle \Omega _{k}}$ is an vertical strip. Then we find a solution ${\textstyle u}$ of the 2D Poison problem such ${\textstyle u=\sum _{k=1}^{M}u_{k}}$, where ${\textstyle u_{k}}$ is the solution of the problem over the strip ${\textstyle \Omega _{k}}$. In practice, we solve the discrete problem (12) over the computational domain ${\textstyle \Omega ^{h}}$ with step size ${\textstyle h}$, which is decomposed into ${\textstyle M}$ sub-grids ${\textstyle \Omega _{k}^{h}}$, see Figure 4(a).

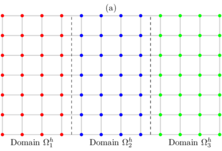
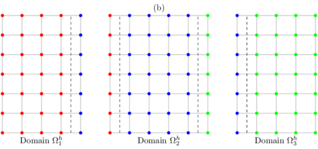
Figure 4: Sketch of rectangular domain decomposition into smaller sub-domains with overlapping grid points.

The compact IFD numerical scheme using the MCSOR method, combined with the domain decomposition method, requires that each element of the sub-domain obtains information from its nine neighbors in each iteration. Consequently, the boundary (or artificial boundary) approximations of each sub-domain need information from the elements in the columns of neighboring sub-domains. This presents a challenge when parallelizing the scheme, as the processes computing the solution in one part of the domain do not have direct access to the memory of other processes. To address this issue, we propose creating sub-domains that overlap, ensuring they include the adjacent neighboring elements, see Figure 4(b). The adjacent information is exchanged using the Message Passing Interface (MPI), meaning that neighboring processors communicate with each other. These communications occur after each sub-step of the MCSOR solver within each sub-domain.

4 Numerical examples

In this section, we perform several tests to analyze the capabilities of the numerical scheme and describe the differences between standard finite difference methods and the implicit finite difference method within the parallel paradigm.

The error is analyzed by comparing the exact and numerical solutions, and it is measured using the ${\textstyle l^{\infty }}$- and ${\textstyle l^{2}}$-norms at all grid points. The order of accuracy is calculated as follows:

${\textrm {Order}}:={\dfrac {\log(\Vert \cdot \Vert _{N_{1}}/\Vert \cdot \Vert _{N_{2}})}{\log(N_{2}/N_{1})}},$

(21)

where ${\textstyle \Vert \cdot \Vert _{N_{1}}}$ and ${\textstyle \Vert \cdot \Vert _{N_{2}}}$ represent the error norms with a resolution relative to grid resolution ${\textstyle N_{1}}$ and ${\textstyle N_{2}}$ respectively.

Next, we conduct several examples to test the robustness of the proposed methodology. We present different examples using iterative solvers such as Jacobi, SOR, RBSOR, and MCSOR methods to find the solutions of the resulting linear system. However, only Jacobi, RBSOR, and MCSOR are suitable for parallelization.

4.1 Example 1

In this example, we show that the numerical method can recover the numerical solution with great accuracy. We consider the 2D Poisson problem over the unit square ${\textstyle \Omega =[0,1]\times [0,1]}$ given by

$u_{xx}+u_{yy}=-8\pi ^{2}\sin(2\pi x)\sin(2\pi y),\quad (x,y)\in (0,1)\times (0,1),$ (22) $u(x,y)=0,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;(x,y)\in \partial \Omega {.}$ (23)

Notice that we impose the Dirichlet boundary conditions at the boundary ${\textstyle \partial \Omega }$. The exact solution of problem (22) and (23) is given by the function

$u(x,y)=\sin(2\pi x)\sin(2\pi y),\quad (x,y)\in \Omega {.}$

Figure 5 shows the numerical and the absolute error for example using a grid resolution with ${\textstyle N=80}$. Notice that even when we use a coarse grid resolution, we obtain an accurate numerical solution. Table 1 shows the convergence analysis for Example 1. As expected, the numerical order for the FD and IFD methods corresponds to second- and fourth-order accuracy, respectively. This confirms that the proposed IFD scheme provides an accurate approximation.

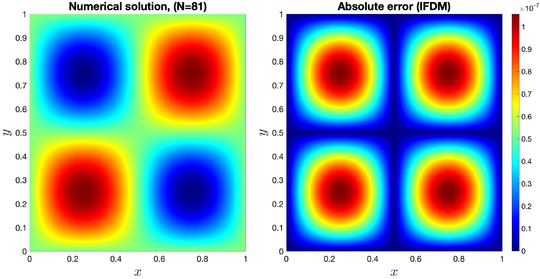
Figure 5: The numerical solution and the absolute error for Example 1 using a grid resolution with $N=80$.

Table. 1 Norm errors and accuracy orders for different values of $N$ in FD and IFD methods.

	FD ($b=0$)				IFD ($b=1/2$)
N	$l^{\infty }$-norm	Order	$l^{2}$-norm	Order	$l^{\infty }$-norm	Order	$l^{2}$-norm	Order
20	8.27E-03	–-	4.13E-02	–-	2.69E-05	–-	1.34E-05	–-
40	2.06E-03	2.01	1.03E-02	2.01	1.69E-06	3.99	8.44E-07	3.99
80	5.14E-04	2.00	2.57E-03	2.00	1.06E-07	4.00	5.28E-08	4.00
160	1.29E-04	2.00	6.43E-04	2.00	6.64E-09	4.00	3.30E-09	4.00
320	3.21E-05	2.00	1.61E-04	2.00	4.44E-10	3.98	2.06E-010	4.00

The SOR iterative solver has a parameter ${\textstyle 0<\omega {<2}}$ that can be tuned to improve performance. Figure 6 illustrates how the number of iterations depends on the parameter ${\textstyle \omega }$ for a given tolerance of ${\textstyle \varepsilon =10^{-9}}$ and a grid resolution of ${\textstyle N=320}$. Figure 6(a) compares the FD and IFD methods, showing that the implicit method not only provides better accuracy but also achieves greater efficiency in terms of the number of iterations required for convergence when the using SOR method. Figure 6(b) shows that both multicolor methods exhibit similar behavior to the standard SOR method. Here, MCSOR requires fewer iterations for convergence compared to RBSOR.

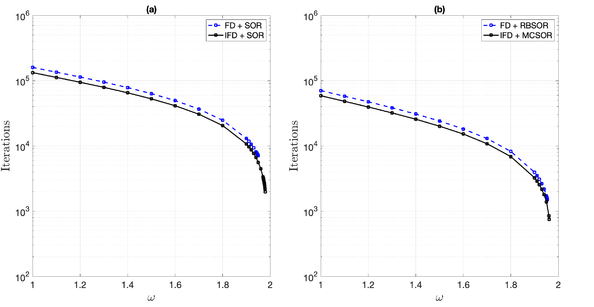
Figure 6: Iterations for the corresponding $\omega$ were performed to achieve a tolerance of $\varepsilon =10^{-9}$ in Example 1, utilizing a grid resolution of $N=320$.

Figure 7(a) shows residual errors for the SOR and Multicolor SOR methods with ${\textstyle \omega =1.8}$ and a grid resolution of ${\textstyle N=320}$. As expected, in all methods, the residual errors decrease as the number of iterations increases, with the IFD methods offering better efficiency in terms of requiring fewer iterations. On the other hand, Figure 7(b) shows the ${\textstyle l^{\infty }}$-norm of the absolute error between the numerical and exact solutions of the problem. Note that the IFD method not only improves efficiency but also offers greater accuracy, a distinct advantage inherent to this implicit technique. Although the results are not shown here, the Jacobi iteration solver demonstrates similar behavior between the IFD and FD methods.

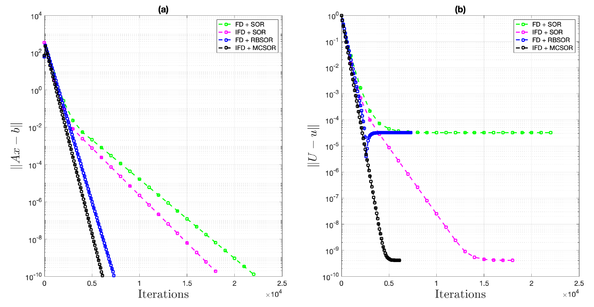
Figure 7: The $l^{\infty }$-norm of residual errors ($\Vert Ax-b\Vert$) for the iterative solvers and their corresponding $l^{\infty }$-norm of absolute errors ($\Vert U-u\Vert$) are shown for $\omega =1.8$, with a tolerance of $\varepsilon =10^{-9}$ and a grid resolution of $N=320$ for Example 1.

4.2 Example 2

In the second example, we test our numerical scheme on a more challenging problem characterized by oscillatory behavior, a key aspect often encountered in computational fluid dynamics simulations. Here, we demonstrate not only the performance of the parallel implementation of the implicit finite-difference method but also a comparison with the standard central finite-difference method (the five-point stencil scheme).

Let us consider the 2D Poisson problem over the unit square ${\textstyle \Omega }$ defined by

$u_{xx}+u_{yy}=-800\pi ^{2}\sin(20\pi x)\sin(20\pi y),\quad (x,y)\in (0,1)\times (0,1)$ (24) $u(x,y)=0,\qquad \qquad \quad \quad \quad \quad \quad \quad \quad \quad \;\;(x,y)\in \partial \Omega {.}$ (25)

Notice that we impose the Dirichlet boundary conditions at the boundary ${\textstyle \partial \Omega }$. Here, the exact solution of problem (24) and (25) is given by the function

$u(x,y)=\sin(20\pi x)\sin(20\pi y),\quad (x,y)\in \Omega {.}$

Problems with large oscillations (high frequency) bring challenges for numerical approximation, as capturing these oscillations accurately requires a large number of grid points. While this may seem like a minor issue for static problems, it becomes significant when solving large Poisson problems as part of evolutionary simulations, such as those involving the Navier-Stokes equations over long time periods.

Figure 8 shows the exact solution and the absolute errors obtained from both the standard and implicit finite difference schemes using a resolution of ${\textstyle N=80}$. As expected, the implicit method yields an accurate approximation. It is also noteworthy that, in both cases, the errors are distributed throughout the entire domain.

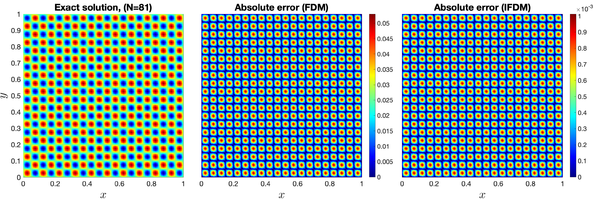
Figure 8: The exact solution and absolute errors for the FD and IFD schemes corresponding to Example 2, using a grid resolution of $N=80$.

Table 2 shows the norm errors and simulation time in seconds of the proposed FD methods using a stopping criterion of ${\textstyle \varepsilon =10^{-9}}$ and ${\textstyle \omega =1.85}$. Similar to the previous example, IFD shows higher accuracy as the standard FD method. For instance, to obtain an approximation with an absolute error less than ${\textstyle 10^{-3}}$, results shows that the FD method requires ${\textstyle N=640}$ grid points, whereas the IFD method only needs ${\textstyle N=160}$ grid points. Furthermore, the computational time required to achieve this absolute error using the Jacobi method with the FD method (47.24 seconds) is approximately 337 times longer than with the IFD method (0.14 seconds). On the other hand, using more advanced and faster solvers such as RBSOR and MCSOR provides the same precision, but both are significantly faster than the Jacobi method. For instance, MCSOR is approximately 30 times faster than Jacobi when using ${\textstyle N=640}$.

Table. 2 Absolute errors and performance for various resolutions of $N$ for the FD and IFD methods using a single processor.

	FD ($b=0$)				IFD ($b=1/2$)
N	$l^{\infty }$-norm	$l^{2}$-norm	Jacobi (sec.)	RBSOR(sec.)	$l^{\infty }$-norm	$l^{2}$-norm	Jacobi(sec.)	MCSOR(sec.)
40	2.34E-01	1.17E-01	0.000125	0.00424	1.30E-02	6.52E-03	0.000131	0.00539
80	5.30E-02	2.65E-02	0.01	0.0173	1.01E-03	5.07E-04	0.00878	0.0224
160	1.30E-02	6.48E-03	0.17	0.0683	6.54E-05	3.27E-05	0.14	0.0956
320	3.22E-03	1.61E-03	2.81	0.28	4.13E-06	2.06E-06	2.42	0.39
640	8.04E-04	4.02E-04	47.24	1.19	2.58E-07	1.29E-07	39.91	1.58

4.2.1 Parallel performance

To analyze the performance of the proposed method, the resolution of the numerical problem will be set into ${\textstyle N=641}$ and ${\textstyle N=1281}$ (more than 400 thousand and 1.6 million of grid points, respectively). The stopping criterion is set to ${\textstyle \varepsilon =10^{-9}}$. This stringent tolerance is selected to ensure that both FD and IFD methods reach their theoretical absolute error.

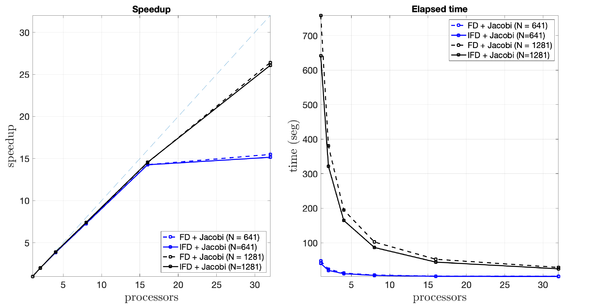
Figure 9: The speedup and elapsed time for the FD and IFD schemes at different resolutions are analyzed using various numbers of processors and the Jacobi solver, with a tolerance of $\varepsilon =10^{-9}$.

Figure 9 shows the speedup and elapsed time for solving the 2D Poisson problem using different schemes and resolutions with the Jacobi solver. Note that the speedup and elapsed time are nearly identical in both cases; however, the IFD method yields more accurate results. In this case, the maximum error for the FD method is approximately ${\textstyle 10^{-4}}$, while for the same setting with the IFD method, the maximum error is close to ${\textstyle 10^{-6}}$. Finally, it is worth noting that the computational time with 32 processors is 24.6 seconds, which is 26 times faster than the sequential solver (641.46 seconds) when using the IFD with ${\textstyle N=1281}$. This represents a reduction of nearly 96% in the original runtime.

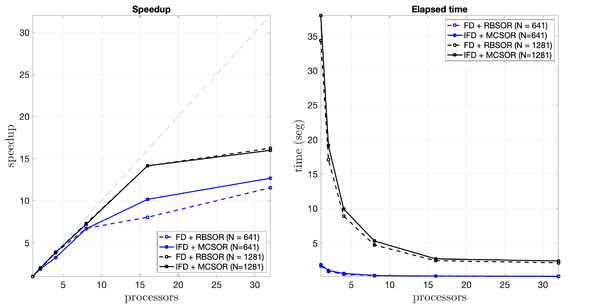
Figure 10 illustrates the performance for the RBSOR and MCSOR solvers. It is important to note that RBSOR and MCSOR are quite different solvers, as they consider the stencil structure for both FD and IFD techniques. Therefore, they recover the solution by accessing the global matrix in different ways and perform different arithmetic operations. However, both methods achieve the same accuracy as described for the Jacobi solver. In terms of parallel performance, the MCSOR method achieves a computational time of 2.37 seconds with 32 processors, making it 16 times faster than the sequential solver (37.99 seconds) for the IFD with ${\textstyle N=1281}$. This represents a nearly 94% reduction compared to MCSOR on a single processor. Moreover, this parallel execution is 270 times faster than the sequential Jacobi solver, yielding a 99.6% reduction in runtime.

Figure 10: The speedup and elapsed time for the FD and IFD schemes at different resolutions are evaluated using various numbers of processors and the RBSOR and MCSOR solvers, with a tolerance of $\varepsilon =10^{-9}$.

5 Conclusions

We present an implicit finite-difference scheme combined with domain decomposition and the Multicolor SOR method for solving the 2D Poisson equation. This scheme provides a fourth-order approximation, consistent with its sequential counterpart. Our experiments demonstrate that, under the same conditions, the IFD method produces more accurate solutions than the standard finite-difference method. Moreover, the speedup and elapsed time are comparable for both numerical schemes, making the IFD method an attractive option since it delivers better results with the same computational effort. In future work, we propose developing a sixth-order implicit finite-difference scheme to solve 2D and 3D Poisson problems.

Acknowledgments

This work was partially supported by the Consejo Nacional de Humanidades, Ciencias y Tecnologías (CONAHCYT) under the program Investigadores e Investigadoras por México, and CONAHCYT México under Ciencia de Frontera Project Number: CF-2023-I-2639. We also acknowledge to the supercomputer facilities provided by CIMAT, specifically Cluster Merida TOLOK, for their invaluable support in conducting our research.

BIBLIOGRAPHY

[1] H.J. Diersch, C.A.J. Fletcher, Computational Techniques for Fluid Dynamics. Vol. I: Fundamental and General Techniques. Vol. II: Specific Techniques for Different Flow Categories, Springer-Verlag, 1988.

[2] Douglas, C. C., Haase, G., & Langer, U. (2003). A tutorial on elliptic PDE solvers and their parallelization. Society for Industrial and Applied Mathematics.

[3] A. Toselli and O. Widlund, Domain decomposition methods–algorithms and theory, Springer-Verlag, Berlin, 2005.

[4] D. M. Young, Iterative solution of large linear systems, Academic Press, New York, 1971.

[5] Uh Zapata, M., & Itzá Balam, R. (2017). High-order implicit finite difference schemes for the two-dimensional Poisson equation. Applied Mathematics and Computation, 309, 222-244.

[6] Adams, L.M., Ortega, J. (1982). A multi-color SOR method for parallel computation, Proc. 1982 Internat. Conf. on Parallel Processing, Bellaire, MI, 53–58.

[7] Zhang, J., Ge, L., & Kouatchou, J. (2000). A two colorable fourth-order compact difference scheme and parallel iterative solution of the 3D convection diffusion equation. Mathematics and Computers in simulation, 54(1-3), 65-80.

[8] Li, Z. H., Chen, L., & Tao, W. Q. (2017). A parallel scalable multigrid method and HOC scheme for anisotropy elliptic problems. Numerical Heat Transfer, Part B: Fundamentals, 71(4), 346-358.

[9] Deka, D., & Sen, S. (2022). Compact higher order discretization of 3D generalized convection diffusion equation with variable coefficients in nonuniform grids. Applied Mathematics and Computation, 413, 126652.

[10] Uh Zapata, M., Pham Van Bang, D., & Nguyen, K. D. (2016). Parallel SOR methods with a parabolic-diffusion acceleration technique for solving an unstructured-grid Poisson equation on 3D arbitrary geometries. International Journal of Computational Fluid Dynamics, 30(5), 370-385.